
家庭们亚 1.认识三确形 第1课时 三角形的角
1.认识三角形 第1课时 三角形的角

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.由不在同一直线上的三条线段首尾顺次相接所组成 的图形叫做三角形组成三角形的三条线段就是三角形的边; 相邻两边的公共端点叫三角形的顶点.相邻两边组成 的角,叫做三角形的内角,简称三角形的角 2.三角形三个内角的和等于180° 导航页
导航页 基础自主梳理 1.由 的三条线段首尾顺次相接所组成 的图形叫做三角形.组成三角形的三条线段就是三角形的边; 相邻两边的公共端点叫三角形的 .相邻两边组成 的角,叫做三角形的内角,简称三角形的角. 2.三角形三个内角的和等于 . 不在同一直线上 顶点 180°

基础自主梳理 3.按三角形内角的大小把三角形分为三类: 锐角三角形:三个内角都是锐角 三角形直角三角形:有一个内角是直角 钝角三角形:有一个内角是钝角 导航页
导航页 基础自主梳理 三角形 锐角三角形:三个内角都是锐角 直角三角形:有一个内角是直角 钝角三角形:有一个内角是 3.按三角形内角的大小把三角形分为三类: 钝角

基出自主梳理 温馨提示 根据三角形的内角判定三角形的形状,主要是根据三个内角 中最大的内角确定:(1)若最大内角为锐角,则三角形为锐角三 角形;(2)若最大内角为直角,则三角形为直角三角形;3)若最 大内角为钝角,则三角形为钝角三角形 导航页
导航页 基础自主梳理 温馨提示 根据三角形的内角判定三角形的形状,主要是根据三个内角 中最大的内角确定:(1)若最大内角为锐角,则三角形为锐角三 角形;(2)若最大内角为直角,则三角形为直角三角形;(3)若最 大内角为钝角,则三角形为钝角三角形

基础自主梳理 4.我们用符号“Rt△ABC”表示“直角三角形ABC”,把直角所 对的边称为直角三角形的 斜 边,夹直角的两条边称 为直角边 5.如图,已知AB LDC,垂足为B. (1)图中的直角三角形有2个,分别是Rt△ABC,Rt△ABD; (2)在Rt△ABC中,直角边是AB,BC 斜边是AC 3)若∠C=35°,则∠BAC= 55°; D 若∠D=65°,则∠DAB= 25° B 导航页
导航页 基础自主梳理 4.我们用符号“Rt△ABC”表示“直角三角形ABC”,把直角所 对的边称为直角三角形的 边,夹直角的两条边称 为 边. 5.如图,已知AB⊥DC,垂足为B. (1)图中的直角三角形有 个,分别是 ; (2)在Rt△ABC中,直角边是 , 斜边是 ; (3)若∠C=35° ,则∠BAC= ; 若∠D=65° ,则∠DAB= . 斜 直角 2 Rt△ABC,Rt△ABD AB,BC AC 55° 25°
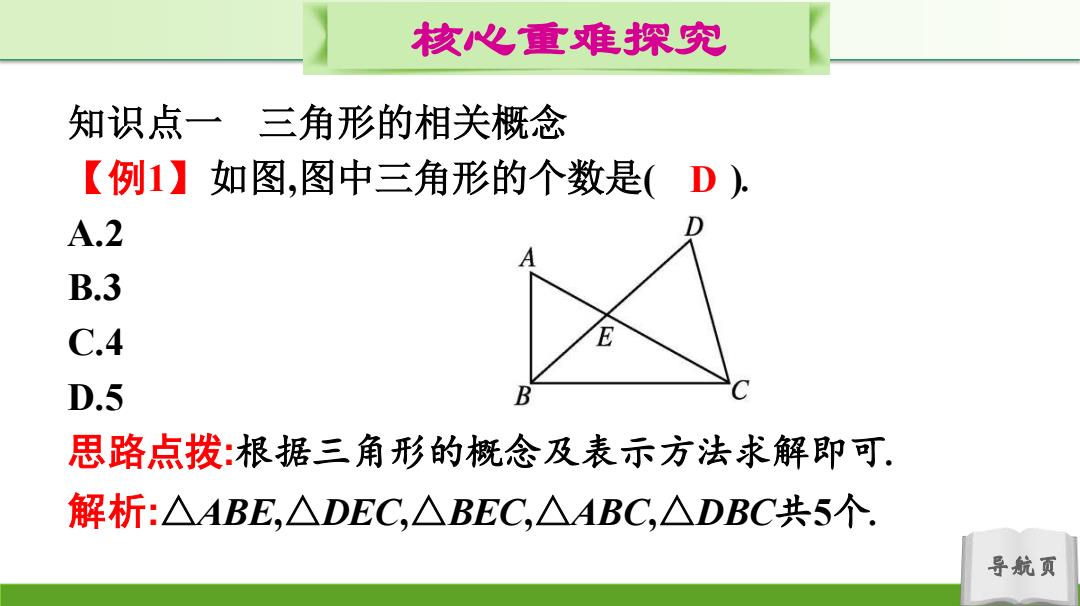
核心重难探究 知识点一三角形的相关概念 【例1】如图,图中三角形的个数是(D), A.2 B.3 C.4 D.5 思路点拨:根据三角形的概念及表示方法求解即可 解析:△ABE,△DEC,△BEC,△ABC,△DBC共5个 导航页
导航页 核心重难探究 知识点一 三角形的相关概念 【例1】如图,图中三角形的个数是( ). A.2 B.3 C.4 D.5 思路点拨:根据三角形的概念及表示方法求解即可. 解析:△ABE,△DEC,△BEC,△ABC,△DBC共5个. D

核心重难探究 【方法归纳】 解答这类问题时,先确定“基础三角形(图中相互不重叠的三 角形)”,再确定由多个三角形组合成的“大的三角形”,这种组 合成的三角形容易被忽略掉,注意不要由于漏掉部分答案而 导致错误 导航页
导航页 核心重难探究 【方法归纳】 解答这类问题时,先确定“基础三角形(图中相互不重叠的三 角形)”,再确定由多个三角形组合成的“大的三角形”,这种组 合成的三角形容易被忽略掉,注意不要由于漏掉部分答案而 导致错误

核心重难探究 知识点二三角形的内角和 【例2】若一个三角形三个内角度数的比为2:7:4,则这个 三角形是( O. A.直角三角形 B.锐角三角形 C钝角三角形 D.等边三角形 思路点拨:先根据三角形内角和求得每个角的度数,然后根 据最大角的度数确定其形状 导航页
导航页 核心重难探究 知识点二 三角形的内角和 【例2】若一个三角形三个内角度数的比为2∶7∶4,则这个 三角形是( ). A.直角三角形 B.锐角三角形 C.钝角三角形 D.等边三角形 思路点拨:先根据三角形内角和求得每个角的度数,然后根 据最大角的度数确定其形状. C

核心心重难探究 解析:三角形三个内角度数的比为2:7:4, .设三角形的三个内角分别为2x,7x,4北 :2x+7x+4x=180,x-180 139 ..7x≈97° ‘这个三角形是钝角三角形 【方法归纳】 根据三角形三个内角的比求各内角度数时,一般通过列方程 求解. 导航页
导航页 核心重难探究 【方法归纳】 根据三角形三个内角的比求各内角度数时,一般通过列方程 求解. 解析:∵三角形三个内角度数的比为2∶7∶4, ∴设三角形的三个内角分别为2x,7x,4x. ∵2x+7x+4x=180,x= 𝟏𝟖𝟎 𝟏𝟑 , ∴7x≈97° . ∴这个三角形是钝角三角形