
家庭作雪 6.完全平方公式 第课时完全平方公式的应用
6.完全平方公式 第2课时 完全平方公式的应用

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升
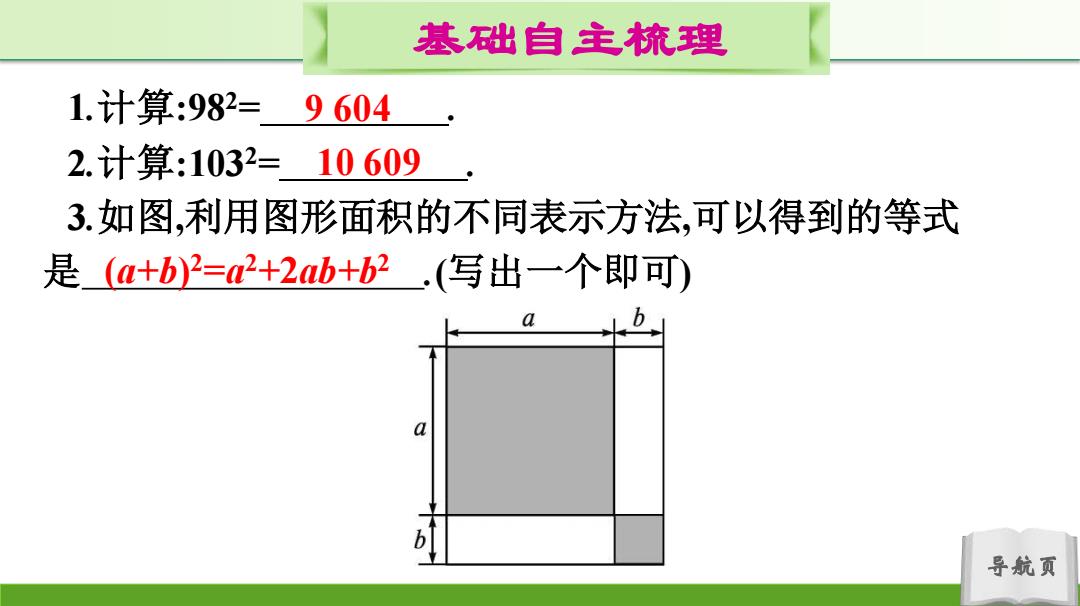
基础自主梳理 1.计算:982=9604 2.计算:1032=10609 3.如图,利用图形面积的不同表示方法,可以得到的等式 是(a+b)2=2+2b+b2.(写出一个即可) a 导航页
导航页 基础自主梳理 1.计算:982= . 2.计算:1032= . 3.如图,利用图形面积的不同表示方法,可以得到的等式 是 .(写出一个即可) 9 604 10 609 (a+b) 2=a2+2ab+b2

核心重难探究 知识点一利用完全平方公式简便计算 【例1】运用公式法计算:2012.401. 思路点拨:先根据完全平方公式对原式进行变形,再解答, 解:2012.401=2012-2×201×1+12=2002=40000, 【方法归纳】 对形如两数和(或差)的平方的计算,都可以用完全平方公式 导航页
导航页 核心重难探究 知识点一 利用完全平方公式简便计算 【例1】运用公式法计算:2012 -401. 思路点拨:先根据完全平方公式对原式进行变形,再解答. 解:2012 -401=2012 -2×201×1+1 2=2002=40 000. 【方法归纳】 对形如两数和(或差)的平方的计算,都可以用完全平方公式

核心重难探究 知识点二利用完全平方公式解决实际问题 【例2】图①是一个长为2m、宽为2的长方形,沿图中虚线用剪刀将其 均分成四个小长方形,然后按图②的方式拼成一个正方形 ()你认为图②中的阴影正方形的边长等于多少? (2)请用两种不同的方法表示 n m 图②中阴影部分的面积 m m m (3)观察图②,你能写出下列三个 m n 代数式之间的等量关系吗? m 代数式:(m+n)2,(m-n)2,4mn. 图① 图 (4)根据3)中的等量关系,解决下面的问题: 若a+b=7,ab=5,求(-b)2的值 导航页
导航页 核心重难探究 知识点二 利用完全平方公式解决实际问题 【例2】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀将其 均分成四个小长方形,然后按图②的方式拼成一个正方形. (1)你认为图②中的阴影正方形的边长等于多少? (2)请用两种不同的方法表示 图②中阴影部分的面积. (3)观察图②,你能写出下列三个 代数式之间的等量关系吗? 代数式:(m+n) 2 ,(m-n) 2 ,4mn. (4)根据(3)中的等量关系,解决下面的问题: 若a+b=7,ab=5,求(a-b) 2的值

核心重难探究 思路点拨:解决这类问题通常是利用数形结合方法(1)观察 图形,可得小正方形的边长;2)根据完全平方公式,可得方法一; 根据完全平方公式的变形,可得方法二3)根据同一图形的面 积相等,可得答案;(4)根据规律求解即可. 导航页
导航页 核心重难探究 思路点拨:解决这类问题通常是利用数形结合方法.(1)观察 图形,可得小正方形的边长;(2)根据完全平方公式,可得方法一; 根据完全平方公式的变形,可得方法二;(3)根据同一图形的面 积相等,可得答案;(4)根据规律求解即可

核心重难探究 解:(1)m-n. (2)(方法一)m-n)2;(方法二)(m叶m2-4mn. (3)(叶n2-4mn=(m-n)2(答案不唯一), (4)(-b)2=(a+b)2-4ab=724×5=29. 【方法归纳】 解决这类问题要数形结合,对几何图形进行整体分析,利用 面积相等求解 导航页
导航页 核心重难探究 解:(1)m-n. (2)(方法一)(m-n) 2 ;(方法二)(m+n) 2 -4mn. (3)(m+n) 2 -4mn=(m-n) 2 (答案不唯一). (4)(a-b) 2=(a+b) 2 -4ab=7 2 -4×5=29. 【方法归纳】 解决这类问题要数形结合,对几何图形进行整体分析,利用 面积相等求解

新知训练织固 1.将边长为acm的正方形的边长增加4cm后,所得新正方形的 面积比原正方形的面积大(D). A.4a cm2 B.(4a+16)cm2 C.Sa cm2 D.(8a+16)cm2 导航页
导航页 新知训练巩固 1.将边长为a cm的正方形的边长增加4 cm后,所得新正方形的 面积比原正方形的面积大( ). A.4a cm2 B.(4a+16)cm2 C.8a cm2 D.(8a+16)cm2 D

新知训练织固 2.如图,通过计算大正方形的面积,可以验证一个等式,这个等 式是(C) A.(x+y+3)2=x2+y2+32+2y+x3+yz X x2 xy XZ B.(x+y+z)2=x2+y2+z+2xy+xz+2yz y xy y2 吹 C.(c+y+z)2=x2+y2+z2+2y+2xz+2yz Z XZ z 22 D.(x+y+z)2=(x+y)2+2xz+2yz 导航页
导航页 新知训练巩固 2.如图,通过计算大正方形的面积,可以验证一个等式,这个等 式是( ). A.(x+y+z) 2=x2+y2+z2+2y+xz+yz B.(x+y+z) 2=x2+y2+z+2xy+xz+2yz C.(x+y+z) 2=x2+y2+z2+2xy+2xz+2yz D.(x+y+z) 2=(x+y) 2+2xz+2yz C

新知训练巩固 3.已知三个圆的位置如图所示,其中m,分别是两个较小圆的 直径,则图中阴影部分的面积为πmn m 导航页
导航页 新知训练巩固 3.已知三个圆的位置如图所示,其中m,n分别是两个较小圆的 直径,则图中阴影部分的面积为 . 𝟏 𝟐 πmn