
家庭值亚 6 应用一元一次方程一一追赶小明
6 应用一元一次方程——追赶小明

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自住梳理 1.行程问题中路程、速度和时间三个量之间的关系是路程= X
基础自主梳理 1.行程问题中路程、速度和时间三个量之间的关系是路程= 速度 ×时间

知识拓展 1.行程问题有相遇问题、追及问题、顺逆流问题、上下坡 问题等.在运动形式上分直线运动和曲线运动(如环形跑道), 相遇问题的特点是相向而行,相遇距离为两运动物体的距离 和.追及问题的特点是同向而行,有两种:慢的在快的前面或慢 的先行若干时间,快的再追及,快=5慢5追及距离顺逆流、顺风 逆风、上下坡应注意运动方向,若去时顺流,则回时为逆流 2.解决行程问题通常利用画线段图的方法
知识拓展 1.行程问题有相遇问题、追及问题、顺逆流问题、上下坡 问题等.在运动形式上分直线运动和曲线运动(如环形跑道). 相遇问题的特点是相向而行,相遇距离为两运动物体的距离 和.追及问题的特点是同向而行,有两种:慢的在快的前面或慢 的先行若干时间,快的再追及,s快=s慢+s追及距离.顺逆流、顺风 逆风、上下坡应注意运动方向,若去时顺流,则回时为逆流. 2.解决行程问题通常利用画线段图的方法

2.一队学生去校外进行训练,他们以5千米时的速度行进,走 了18分钟的时候,学校要将一个紧急通知传给队长,通讯员从 学校出发,骑自行车以14千米时的速度按原路追上去,通讯员 需多长时间可以追上学生队伍? 解:设通讯员需要X小时可以追上学生队伍, 根据惠毫,得145x2品x5. 鲜得合 苍:通讯员需要小时可以追上学生队伍. 合
2.一队学生去校外进行训练,他们以5千米/时的速度行进,走 了18分钟的时候,学校要将一个紧急通知传给队长,通讯员从 学校出发,骑自行车以14千米/时的速度按原路追上去,通讯员 需多长时间可以追上学生队伍? 解:设通讯员需要 x 小时可以追上学生队伍, 根据题意,得 14x-5x=𝟏𝟖 𝟔𝟎 ×5. 解得 x= 𝟏 𝟔 . 答:通讯员需要𝟏 𝟔 小时可以追上学生队伍

核心重难探究 知识点一直线型相遇问题 【例1】已知甲、乙两地相距240千米,汽车从甲地开往乙 地,速度为36千米时;摩托车从乙地开往甲地,速度是汽车速 度的.摩托车从乙地出发2小时30分钟后,汽车开始从甲地开 往乙地,经过几小时汽车与摩托车相遇?
核心重难探究 知识点一 直线型相遇问题 【例1】已知甲、乙两地相距240千米,汽车从甲地开往乙 地,速度为36千米/时;摩托车从乙地开往甲地,速度是汽车速 度的 .摩托车从乙地出发2小时30分钟后,汽车开始从甲地开 往乙地,经过几小时汽车与摩托车相遇? 𝟐 𝟑
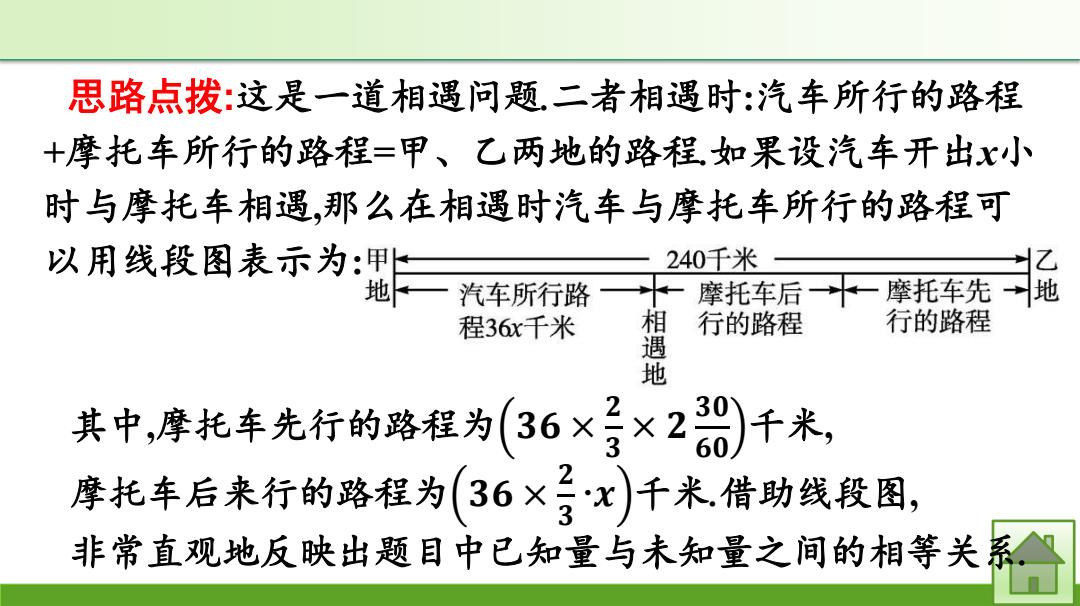
思路点拨:这是一道相遇问题.二者相遇时:汽车所行的路程 +摩托车所行的路程=甲、乙两地的路程如果设汽车开出x小 时与摩托车相遇,那么在相遇时汽车与摩托车所行的路程可 以用线段图表示为:甲 240千米 汽车所行路 摩托车后 摩托车先 地 程36x千米 行的路程 行的路程 地 其中,摩托车先行的路程为(36×号×2 千米, 摩托车后来行的路程为(36×子x)千米借助线段图, 非常直观地反映出题目中已知量与未知量之间的相等关系
思路点拨:这是一道相遇问题.二者相遇时:汽车所行的路程 +摩托车所行的路程=甲、乙两地的路程.如果设汽车开出x小 时与摩托车相遇,那么在相遇时汽车与摩托车所行的路程可 以用线段图表示为: 其中,摩托车先行的路程为 𝟑𝟔 × 𝟐 𝟑 × 𝟐 𝟑𝟎 𝟔𝟎 千米, 摩托车后来行的路程为 𝟑𝟔 × 𝟐 𝟑 ·𝒙 千米.借助线段图, 非常直观地反映出题目中已知量与未知量之间的相等关系

解:设汽车径过x小时与摩托车相遇, 则根据惠意,得36x+36X号+36号28240. 解方程,得x=3. 因此,汽车经过3小时与摩托车相遇
解:设汽车经过x小时与摩托车相遇, 则根据题意,得 36x+36× 𝟐 𝟑 ·x+36× 𝟐 𝟑 ×2 𝟑𝟎 𝟔𝟎 =240. 解方程,得x=3. 因此,汽车经过3小时与摩托车相遇

【解题规律】 在相遇问题中,两人同时相向而行的路程之和等于两人相距 的路程;在追及问题中,双方是同向而行,“同时不同地”的追 及问题,双方行走所用时间相同,行走的路程却不同(出发点不 同);而“同地不同时”,由于行走双方出发时间有先后,故行走 过程中用的时间不同,双方出发地相同,故行走的路程相同
【解题规律】 在相遇问题中,两人同时相向而行的路程之和等于两人相距 的路程;在“追及问题”中,双方是同向而行,“同时不同地”的追 及问题,双方行走所用时间相同,行走的路程却不同(出发点不 同);而“同地不同时”,由于行走双方出发时间有先后,故行走 过程中用的时间不同,双方出发地相同,故行走的路程相同

知识点二环形跑道问题 【例2】暑假里,小亮去体育场晨练,每天都见到一名田径队 的叔叔也在锻炼两人沿400米跑道跑步,每次总是小亮跑2圈 的时间,叔叔跑3圈. ()一天,两人同时同地反向而跑,小亮看了一下时间,发现隔 了32秒钟两人第一次相遇求两人的速度 (2)如果小亮和叔叔在同地同时同向而跑,那么叔叔隔多长 时间第一次与小亮相遇?
知识点二 环形跑道问题 【例2】暑假里,小亮去体育场晨练,每天都见到一名田径队 的叔叔也在锻炼.两人沿400米跑道跑步,每次总是小亮跑2圈 的时间,叔叔跑3圈. (1)一天,两人同时同地反向而跑,小亮看了一下时间,发现隔 了32秒钟两人第一次相遇.求两人的速度. (2)如果小亮和叔叔在同地同时同向而跑,那么叔叔隔多长 时间第一次与小亮相遇?