
家庭值少 2 比较线段的长短
2 比较线段的长短

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.(1)两点之间的所有连线中,线段最短.这一事实可以简述 为: (2)两点之间线段的 叫做这两点之间的距离. 名师指导 1.两点之间的连线,可能是笔直的,也可能是弯曲的,在这些 线中,两点之间的线段是最短的 2.“线段”是几何图形,而“线段的长度”是一个正的数值,两者 是不同的
基础自主梳理 1.(1)两点之间的所有连线中,线段最短.这一事实可以简述 为:两点之间线段最短 . (2)两点之间线段的长度 ,叫做这两点之间的距离. 名师指导 1.两点之间的连线,可能是笔直的,也可能是弯曲的,在这些 线中,两点之间的线段是最短的. 2. “线段”是几何图形,而“线段的长度”是一个正的数值,两者 是不同的

2.(1)只用没有刻度的直尺和圆规画图称为尺规作图.我们先 用直尺画射线AC,再用圆规在射线AC上截取AB=,这就是 “作一条线段等于已知线段”的尺规作图, (2)比较两条线段的长短,我们有两种方法:一种方法是用刻 度尺量出它们的 ,再进行比较;另一种方法是把其中的 一条线段 另一条线段上去,将其中的一个端点重合在 一起加以比较 3)点M把线段AB分成 的两条线段AM与MB,点M叫 做线段AB的中点类似地,还有线段的三等分点、四等分点等
2.(1)只用没有刻度的直尺和圆规画图称为尺规作图.我们先 用直尺画射线AC,再用圆规在射线AC上截取AB=a,这就是 “作一条线段等于已知线段”的尺规作图. (2)比较两条线段的长短,我们有两种方法:一种方法是用刻 度尺量出它们的长度 ,再进行比较;另一种方法是把其中的 一条线段移到 另一条线段上去,将其中的一个端点重合在 一起加以比较. (3)点M把线段AB分成相等 的两条线段AM与MB,点M叫 做线段AB的中点.类似地,还有线段的三等分点、四等分点等

核心重难探究 知识点一线段的基本事实 【例1】平面上有A,B,C,D四个村庄,为解决当地缺水问题, 政府准备投资修建一个蓄水池,不考虑其他因素,请你画图确 定蓄水池H的位置,使它与四个村庄的距离之和最小 D 4 C ·B 合
核心重难探究 知识点一 线段的基本事实 【例1】平面上有A,B,C,D四个村庄,为解决当地缺水问题, 政府准备投资修建一个蓄水池,不考虑其他因素,请你画图确 定蓄水池H的位置,使它与四个村庄的距离之和最小

思路点拨:到A,C两点距离之和最短的点在哪里?到B,D两点 距离之和最短的点在哪里?由此你能同时确定到A,B,C,D四个 点的距离之和最短的点在哪里吗?
思路点拨:到A,C两点距离之和最短的点在哪里?到B,D两点 距离之和最短的点在哪里?由此你能同时确定到A,B,C,D四个 点的距离之和最短的点在哪里吗?
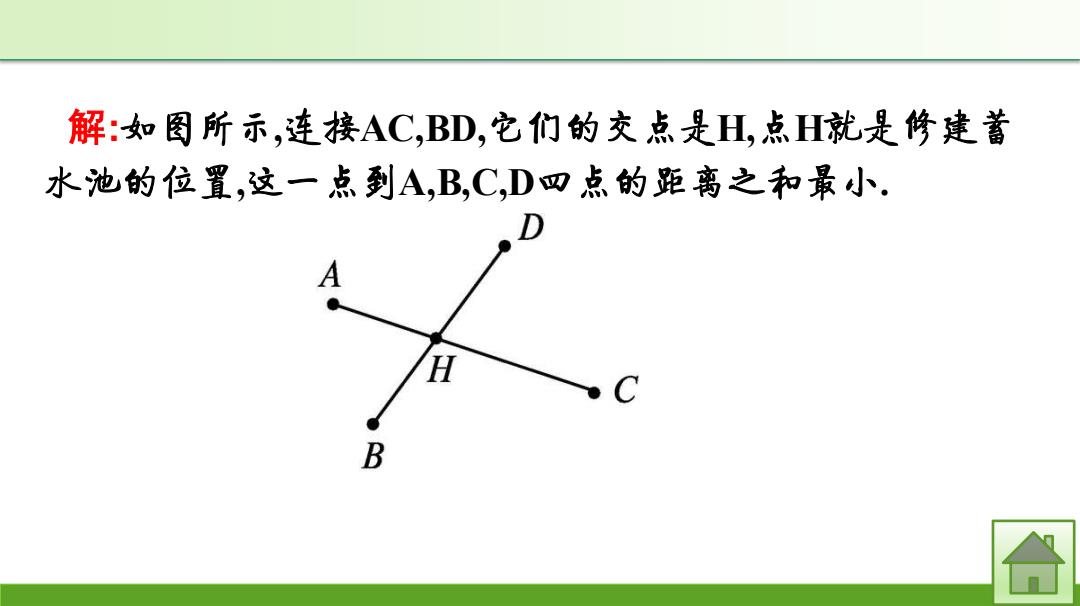
解:如图所示,连接AC,BD,它们的交点是H,点H就是修建蓄 水池的位置,这一点到A,B,C,D四点的距离之和最小. A H C B
解:如图所示,连接AC,BD,它们的交点是H,点H就是修建蓄 水池的位置,这一点到A,B,C,D四点的距离之和最小

【名师点津】 利用“两点之间线段最短”的性质,可以找到到几点的路程之 和最小的一点. 合
【名师点津】 利用“两点之间线段最短”的性质,可以找到到几点的路程之 和最小的一点

知识点二作已知线段的和或差 【例2】如图,已知线段,b,用直尺和圆规求作一条线段AB, 使AB=2a-b. a b 思路点拨:利用尺规作图的方法,在一条射线上作出线段等 于线段的两倍长,再在所作的线段上截取线段b,剩余部分即 为所求
知识点二 作已知线段的和或差 【例2】如图,已知线段a,b,用直尺和圆规求作一条线段AB, 使AB=2a-b. 思路点拨:利用尺规作图的方法,在一条射线上作出线段等 于线段a的两倍长,再在所作的线段上截取线段b,剩余部分即 为所求

解:作法:1)作射线AP,如图. a a BM N P (2)以A为端点,用圆规在AP上顺次截取AM=MN=a. (3)以N为端点,在线段AN上截取NB=b. 则线段AB即为所求作的线段 合
解:作法:(1)作射线AP,如图. (2)以A为端点,用圆规在AP上顺次截取AM=MN=a. (3)以N为端点,在线段AN上截取NB=b. 则线段AB即为所求作的线段