
家庭馆亚 4角的比较
4 角的比较

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.比较角的大小的常用方法 (1)度量法:用量角器测量出各角的 ,再比较大小 (2)叠合法:将两个角的顶点及一条边,另一条边放在 的同侧就可以比较大小 名师指导 1.使用叠合法时应注意顶点重合,一边重合,另一边落在重合 边的同侧. 2.角的大小关系和角的度数的大小关系是一致的,这是从 “数”的方面来进行比较的
基础自主梳理 1.比较角的大小的常用方法 (1)度量法:用量角器测量出各角的度数,再比较大小. (2)叠合法:将两个角的顶点及一条边重合,另一条边放在 重合边的同侧就可以比较大小. 名师指导 1.使用叠合法时应注意顶点重合,一边重合,另一边落在重合 边的同侧. 2.角的大小关系和角的度数的大小关系是一致的,这是从 “数”的方面来进行比较的

2.小于平角的角可以分为三类:锐角 、钝角。 3.从一个角的顶点引出的一条射线,把这个角分成两个 的角,这条射线叫做这个角的平分线 名师指导 1.若OC平分∠AOB,则可表示为∠AOC=∠BOC,或∠AOC= 1 ∠AOB,或LAOB=2∠AOC: 2.角的平分线应在角的内部,且为一条射线,必须从角的顶点 引出
2.小于平角的角可以分为三类:锐角、直角 、钝角. 3.从一个角的顶点引出的一条射线,把这个角分成两个相等 的角,这条射线叫做这个角的平分线. 名师指导 1.若OC平分∠AOB,则可表示为∠AOC=∠BOC,或∠AOC= ∠AOB,或∠AOB=2∠AOC. 2.角的平分线应在角的内部,且为一条射线,必须从角的顶点 引出. 𝟏 𝟐
核心重难探究 知识点一角的大小比较 【例1】如图,∠AOC=∠BOD=0°. C (1)∠BOD是哪两个角的和?∠DOC是哪两个角的差? (2)∠AOC与∠AOD哪个角更大一些? 3)不用度量的方法,你能猜想∠AOB与∠DOC的大小关系吗? 说说你的理由
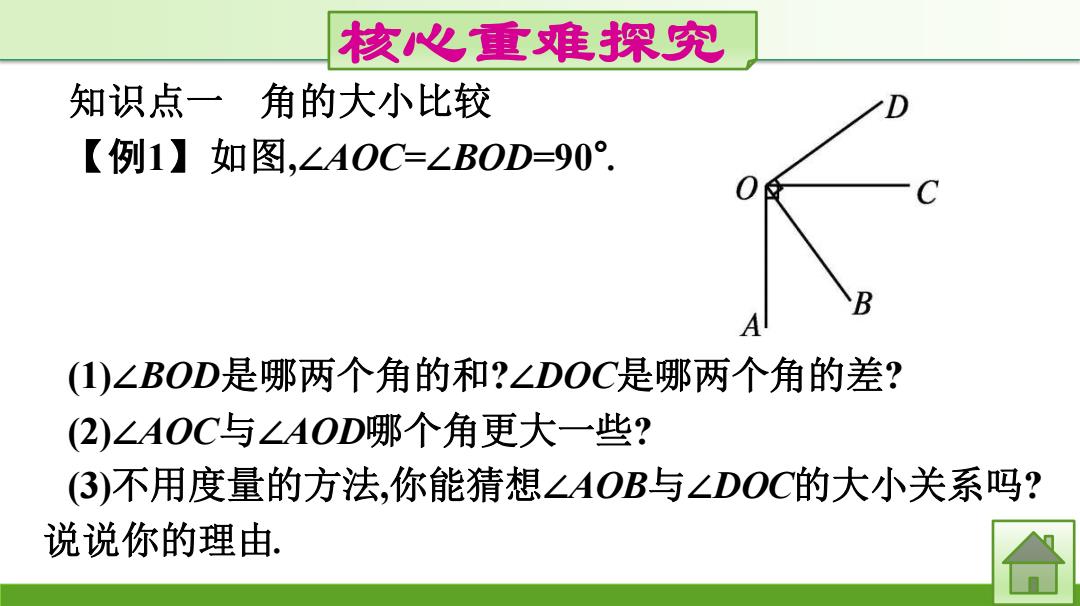
核心重难探究 知识点一 角的大小比较 【例1】如图,∠AOC=∠BOD=90° . (1)∠BOD是哪两个角的和?∠DOC是哪两个角的差? (2)∠AOC与∠AOD哪个角更大一些? (3)不用度量的方法,你能猜想∠AOB与∠DOC的大小关系吗? 说说你的理由

思路点拨:(1)∠BOD内部的射线OC把该角分成了哪两个角? 射线OC还在哪个角的内部? (2)∠AOC与∠AOD哪条边重合?另一条边有何关系? 3)∠AOB与∠DOC分别与∠BOC有何关系? 合
思路点拨:(1)∠BOD内部的射线OC把该角分成了哪两个角? 射线OC还在哪个角的内部? (2)∠AOC与∠AOD哪条边重合?另一条边有何关系? (3)∠AOB与∠DOC分别与∠BOC有何关系?

解:1)∠BOD是∠BOC与∠COD的和,∠DOC是∠DOB与 ∠COB,或∠DOA与∠COA的差. (2)∠AOD更大一些. 3)∠AOB=∠DOC.理由: 因为∠AOB=∠AOC-∠BOC=90°-∠BOC,∠DOC=∠DOB- ∠BOC=90°-∠B0C, 所以∠AOB=∠DOC
解:(1)∠BOD是∠BOC与∠COD的和,∠DOC是∠DOB与 ∠COB,或∠DOA与∠COA的差. (2)∠AOD更大一些. (3)∠AOB=∠DOC.理由: 因为∠AOB=∠AOC-∠BOC=90°-∠BOC,∠DOC=∠DOB- ∠BOC=90°-∠BOC, 所以∠AOB=∠DOC

【巧记乐背】 角的和差与倍分,根据图形来理解;一边重合一边动,异侧为 和同侧差 合
【巧记乐背】 角的和差与倍分,根据图形来理解;一边重合一边动,异侧为 和同侧差

知识点二角的运算 【例2】如图,点A,O,B在同一条直线上,直线CD经过点O,已 知∠DOE=∠BOD=∠AOC,OF平分∠AOE,当∠AOC=28°13时, 求∠EOF的度数: A B C
知识点二 角的运算 【例2】如图,点A,O,B在同一条直线上,直线CD经过点O,已 知∠DOE=∠BOD=∠AOC,OF平分∠AOE,当∠AOC= 28°13'时, 求∠EOF的度数

思路点拨:(1)∠EOF与∠AOE有何关系?∠DOE的度数是多少? (2)∠AOE,∠DOE,∠AOC三者有何关系? 合
思路点拨:(1)∠EOF与∠AOE有何关系?∠DOE的度数是多少? (2)∠AOE,∠DOE,∠AOC三者有何关系?