
家庭值业 3 应用一元一次方程一一水箱变高了
3 应用一元一次方程——水箱变高了

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自住梳理 1.(1)长度一定,围成不同形状的图形,应抓住 不变;2)两 种物体混合应用题,混合前后的 不变;3)物体锻造等应用 题,变化前后的 不变 2.用一根长12米的绳子围成了一个长方形,长为5米,若要使 它变成一个正方形,则应将长减少(B) A.1米 B.2米 C.3米 D.4米
基础自主梳理 1.(1)长度一定,围成不同形状的图形,应抓住周长不变;(2)两 种物体混合应用题,混合前后的质量不变;(3)物体锻造等应用 题,变化前后的体积不变. 2.用一根长12米的绳子围成了一个长方形,长为5米,若要使 它变成一个正方形,则应将长减少( ). A.1米 B.2米 C.3米 D.4米 B

核心重难探究 知识点一列一元一次方程解等体积变形问题 【例1】在一个底面直径为5cm、高为18cm的圆柱形玻璃 瓶内装满水,再将瓶内的水完全倒入一个底面直径为6c、 高为13cm的圆柱形杯子中. (1)能否把圆柱形杯子装满?为什么? (2)若装不下,则瓶内水面还有多高?若不能装满,求杯内水面 离杯口的距离:
核心重难探究 知识点一 列一元一次方程解等体积变形问题 【例1】在一个底面直径为5 cm、高为18 cm的圆柱形玻璃 瓶内装满水,再将瓶内的水完全倒入一个底面直径为6 cm、 高为13 cm的圆柱形杯子中. (1)能否把圆柱形杯子装满?为什么? (2)若装不下,则瓶内水面还有多高?若不能装满,求杯内水面 离杯口的距离

思路点拨:本题实际上提出两个问题:()能否装下,就是比较 杯子与瓶子的体积的大小;2)能装下或装不下的情况的具体 问题,这需要在(1)的结论下完成
思路点拨:本题实际上提出两个问题:(1)能否装下,就是比较 杯子与瓶子的体积的大小;(2)能装下或装不下的情况的具体 问题,这需要在(1)的结论下完成

解:0流子的体积:沉×()'x1825cm 杯子的体积:元×)x13=117πcm. 因<17元,所以不能装满杯子. (2)设此时杯子内水的高度为Xcm, 则根据夏意,得π×)x18=π×)2x 解这个方程,得x=12.5.所以13-12.5=0.5(cm). 因此,把瓶内的水倒入杯中不能装满杯子,此时杯内水面离 杯口的距离为0.5cm
解:(1)瓶子的体积:π× 𝟓 𝟐 𝟐 ×18=𝟐𝟐𝟓 𝟐 π(cm3 ); 杯子的体积:π× 𝟔 𝟐 𝟐 ×13=117π(cm3 ). 因为𝟐𝟐𝟓 𝟐 π<117π,所以不能装满杯子. (2)设此时杯子内水的高度为 x cm, 则根据题意,得 π× 𝟓 𝟐 𝟐 ×18=π× 𝟔 𝟐 𝟐 ·x. 解这个方程,得 x=12.5.所以 13-12.5=0.5(cm). 因此,把瓶内的水倒入杯中不能装满杯子,此时杯内水面离 杯口的距离为0.5 cm

【解题规律】 本题的两个问题是紧密相连的.在解决第二个问题时,抓住 了水的体积不变这一等量关系列出方程 合
【解题规律】 本题的两个问题是紧密相连的.在解决第二个问题时,抓住 了水的体积不变这一等量关系列出方程
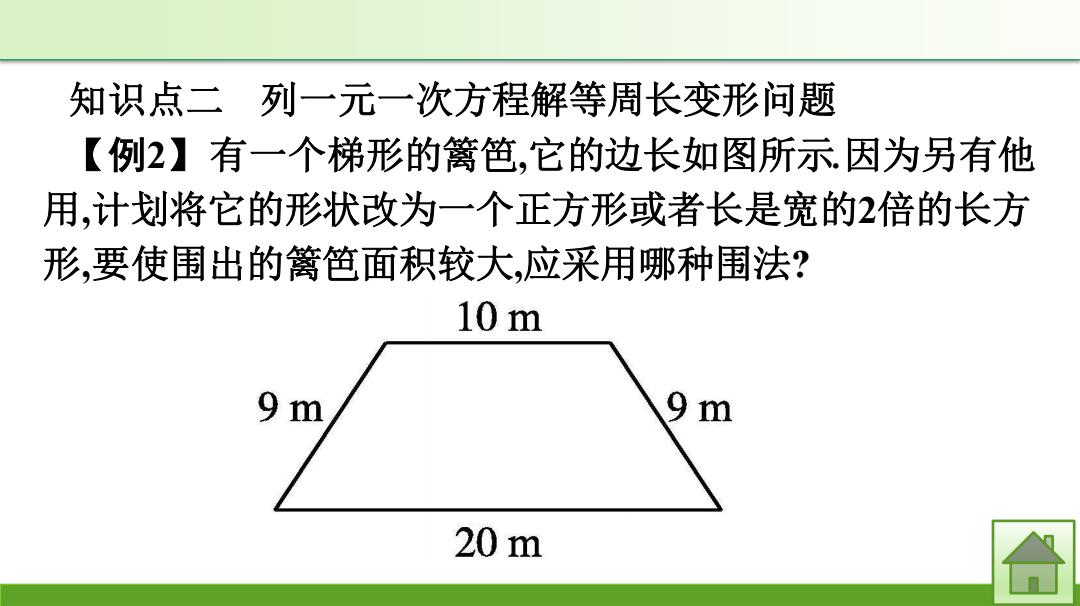
知识点二列一元一次方程解等周长变形问题 【例2】有一个梯形的篱笆,它的边长如图所示因为另有他 用,计划将它的形状改为一个正方形或者长是宽的2倍的长方 形,要使围出的篱笆面积较大,应采用哪种围法? 10m 9 m 9 m 20m 合
知识点二 列一元一次方程解等周长变形问题 【例2】有一个梯形的篱笆,它的边长如图所示.因为另有他 用,计划将它的形状改为一个正方形或者长是宽的2倍的长方 形,要使围出的篱笆面积较大,应采用哪种围法?

思路点拨:本题中的等量关系是“篱笆在形状变化过程中周 长不变”,由此可以采用间接设未知数的方法求解 合
思路点拨:本题中的等量关系是“篱笆在形状变化过程中周 长不变”,由此可以采用间接设未知数的方法求解

解:当篱笆围成正方形时, 因为正方形的边长为10+9牛20+9-12m 4 所以正方形的面积为12×12=144(m2). 当萬笆围成长方形时,设长方形的宽为xm,则长为2xm. 根据题意,得2x+2x)=10+20+9+9. 解方程,得x=8,2x=8X2=16. 所以长方形的面积为8×16=128(m2). 因为144>128,所以围成正方形时面积较大. 因此,要使围出的篱笆面积较大,应围成正方形. 合
解:当篱笆围成正方形时, 因为正方形的边长为𝟏𝟎+𝟗+𝟐𝟎+𝟗 𝟒 =12(m), 所以正方形的面积为12×12=144(m2 ). 当篱笆围成长方形时,设长方形的宽为x m,则长为2x m. 根据题意,得2(x+2x)=10+20+9+9. 解方程,得x=8,2x=8×2=16. 所以长方形的面积为8×16=128(m2 ). 因为144>128,所以围成正方形时面积较大. 因此,要使围出的篱笆面积较大,应围成正方形