
家庭侯亚 2.探索直线平行的条件 第2课时 探索直线平行的系件(2)
2.探索直线平行的条件 第2课时 探索直线平行的条件(2)

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升
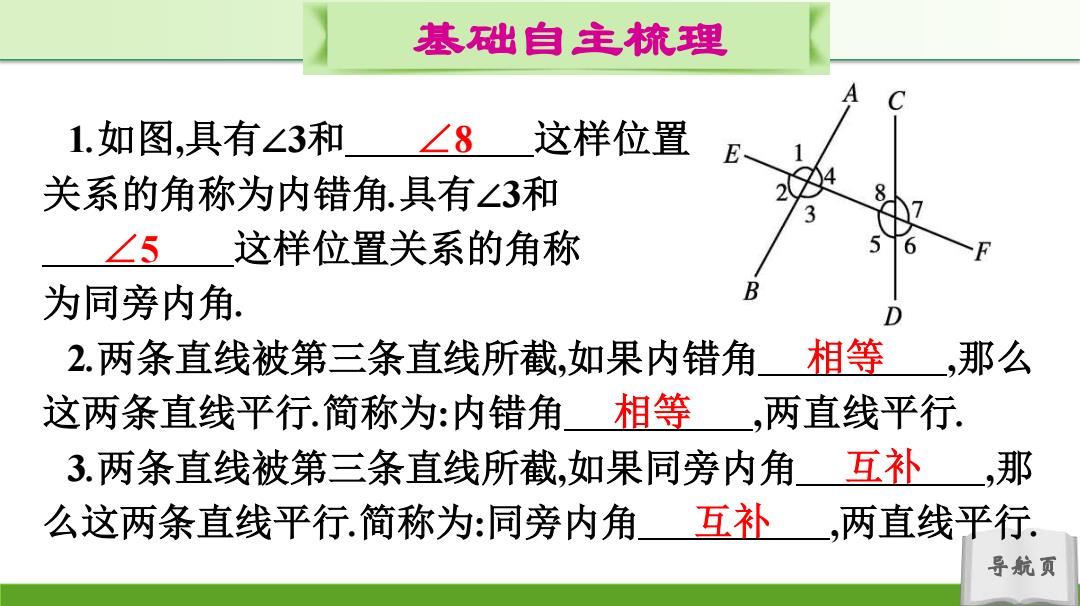
基础自主梳理 1.如图,具有∠3和 ∠8 这样位置 关系的角称为内错角.具有∠3和 ∠5 这样位置关系的角称 为同旁内角. B 2.两条直线被第三条直线所截,如果内错角相等,那么 这两条直线平行简称为:内错角相等,两直线平行! 3.两条直线被第三条直线所截,如果同旁内角互补 那 么这两条直线平行.简称为:同旁内角互补,两直线平行 导航页
导航页 基础自主梳理 1.如图,具有∠3和 这样位置 关系的角称为内错角.具有∠3和 这样位置关系的角称 为同旁内角. 2.两条直线被第三条直线所截,如果内错角 ,那么 这两条直线平行.简称为:内错角 ,两直线平行. 3.两条直线被第三条直线所截,如果同旁内角 ,那 么这两条直线平行.简称为:同旁内角 ,两直线平行. ∠8 ∠5 相等 相等 互补 互补

基础自主梳理 温馨提示 “同旁内角互补”是“两直线平行”的一个前提,在使用时,不 可忽略前提.同时不要出现“同旁内角相等,两直线平行”的错 误 导航页
导航页 基础自主梳理 温馨提示 “同旁内角互补”是“两直线平行”的一个前提,在使用时,不 可忽略前提.同时不要出现“同旁内角相等,两直线平行”的错 误

核心重难探究 知识点一内错角、同旁内角 【例1】如图,下列说法:①∠A与∠B是同旁内角;②∠2与∠1 是内错角;③∠A与∠C是内错角;④∠A与∠1是同位角.其中正 确的个数是( ).C A.1 B.2 C.3 D.4 导航页
导航页 核心重难探究 知识点一 内错角、同旁内角 【例1】如图,下列说法:①∠A 与∠B是同旁内角;②∠2与∠1 是内错角;③∠A与∠C是内错角;④∠A与∠1是同位角.其中正 确的个数是( ). A.1 B.2 C.3 D.4 C

核心心重难探究 思路点拨:两条直线被第三条直线所截,在截线的同旁,被截 两直线的同一方,把这种位置关系的一对角称为同位角:两个 角分别在截线的异侧,且夹在两条被截线之间,具有这样位置 关系的一对角互为内错角;两个角都在截线的同一侧,且在两 条被截线之间,具有这样位置关系的一对角互为同旁内角. 解析:①∠A与∠B是同旁内角,正确;②∠2与∠1是内错角,正确; ③∠A与∠C是内错角,错误,应为同旁内角;④∠A与∠1是同位 角,正确.故选C 导航页
导航页 核心重难探究 思路点拨:两条直线被第三条直线所截,在截线的同旁,被截 两直线的同一方,把这种位置关系的一对角称为同位角;两个 角分别在截线的异侧,且夹在两条被截线之间,具有这样位置 关系的一对角互为内错角;两个角都在截线的同一侧,且在两 条被截线之间,具有这样位置关系的一对角互为同旁内角. 解析:①∠A与∠B是同旁内角,正确;②∠2与∠1是内错角,正确; ③∠A与∠C是内错角,错误,应为同旁内角;④∠A与∠1是同位 角,正确.故选C

核心重难探究 【方法归纳】 在一些复杂的图形中,可以隐去一些不相关的线条,将要研 究的对象从事物的整体中分离出来,单独加以考察、分析、 研究,以免受其干扰,就能很快地求解, 导航页
导航页 核心重难探究 【方法归纳】 在一些复杂的图形中,可以隐去一些不相关的线条,将要研 究的对象从事物的整体中分离出来,单独加以考察、分析、 研究,以免受其干扰,就能很快地求解
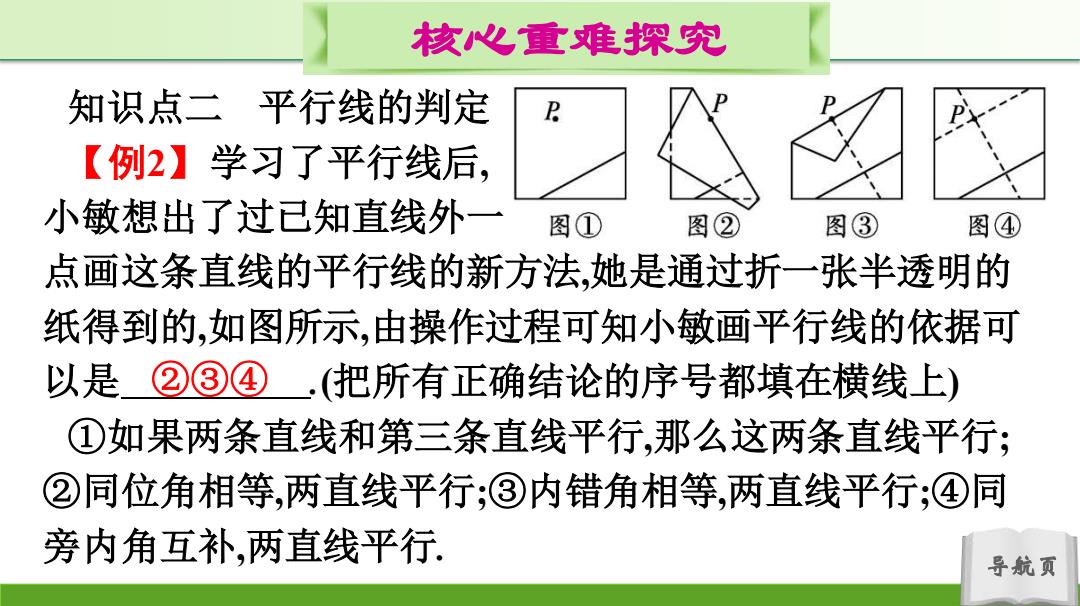
核心重难探究 知识点二平行线的判定 【例2】学习了平行线后, 小敏想出了过已知直线外一 图① 图② 图③ 图④ 点画这条直线的平行线的新方法,她是通过折一张半透明的 纸得到的,如图所示,由操作过程可知小敏画平行线的依据可 以是②③④,(把所有正确结论的序号都填在横线上) ①如果两条直线和第三条直线平行,那么这两条直线平行; ②同位角相等,两直线平行;③内错角相等,两直线平行;④同 旁内角互补,两直线平行 导航页
导航页 核心重难探究 知识点二 平行线的判定 【例2】学习了平行线后, 小敏想出了过已知直线外一 点画这条直线的平行线的新方法,她是通过折一张半透明的 纸得到的,如图所示,由操作过程可知小敏画平行线的依据可 以是 .(把所有正确结论的序号都填在横线上) ①如果两条直线和第三条直线平行,那么这两条直线平行; ②同位角相等,两直线平行;③内错角相等,两直线平行;④同 旁内角互补,两直线平行. ②③④
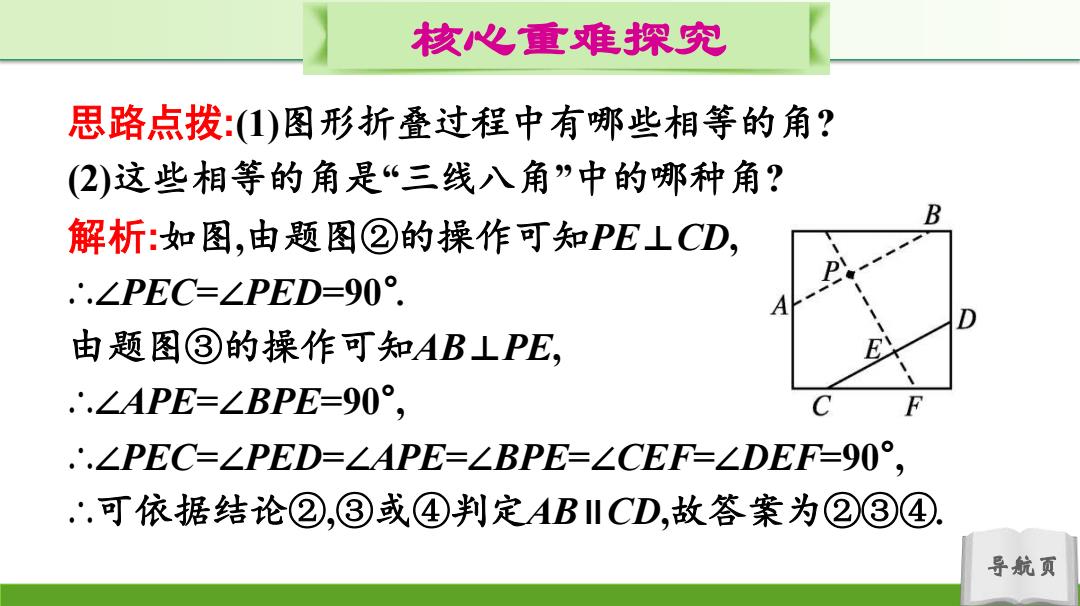
核心心重难探究 思路点拨:()图形折叠过程中有哪些相等的角? (2)这些相等的角是“三线八角”中的哪种角? B 解析:如图,由题图②的操作可知PE LCD, .∴∠PEC=∠PED=90° 由题图③的操作可知AB LPE, ∴.∠APE=∠BPE=90°, .∴.∠PEC=∠PED=∠APE=∠BPE=∠CEF=∠DEF=90°, '.可依据结论②,③或④判定ABIICD,故答案为②③④ 导航页
导航页 核心重难探究 思路点拨:(1)图形折叠过程中有哪些相等的角? (2)这些相等的角是“三线八角”中的哪种角? 解析:如图,由题图②的操作可知PE⊥CD, ∴∠PEC=∠PED=90° . 由题图③的操作可知AB⊥PE, ∴∠APE=∠BPE=90° , ∴∠PEC=∠PED=∠APE=∠BPE=∠CEF=∠DEF=90° , ∴可依据结论②,③或④判定AB∥CD,故答案为②③④

核心重难探究 【方法归纳】 解决本题的关键是理解折叠的过程 导航页
导航页 核心重难探究 【方法归纳】 解决本题的关键是理解折叠的过程