
家庭像四 第五章 生活中的轴对称 2.探索轴对称的性质
第五章 生活中的轴对称 2.探索轴对称的性质

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.在轴对称图形或两个成轴对称的图形中,对应点所连的线 段被对称轴 垂直平分,对应线段相等,对应角相等 温馨提示 如果两个图形关于某条直线对称,那么对称轴是任何一对对 应点所连线段的垂直平分线.类似地,轴对称图形的对称轴,是 任何一对对应点所连线段的垂直平分线。 导航页
导航页 基础自主梳理 1.在轴对称图形或两个成轴对称的图形中,对应点所连的线 段被对称轴 ,对应线段相等,对应角相等. 温馨提示 如果两个图形关于某条直线对称,那么对称轴是任何一对对 应点所连线段的垂直平分线.类似地,轴对称图形的对称轴,是 任何一对对应点所连线段的垂直平分线. 垂直平分

基础自主梳理 2.如果两个图形关于某一条直线对称,且对应的线段或其延 长线相交,那么交点一定在对称轴上 3.作一个图形的轴对称图形的基本步骤是: (1)先找出已知图形中能够确定它的形状的关键点(图形的 顶点、交叉点、拐点等); (2)分别作出这些关键点的对称点; 3)顺次(或根据图形要求)连接所作出的点,即可得到已知图 形的轴对称图形 导航页
导航页 基础自主梳理 2.如果两个图形关于某一条直线对称,且对应的线段或其延 长线相交,那么交点一定在 上. 3.作一个图形的轴对称图形的基本步骤是: (1)先找出已知图形中能够确定它的形状的关键点(图形的 顶点、交叉点、拐点等); (2)分别作出这些关键点的 点; (3)顺次(或根据图形要求)连接所作出的点,即可得到已知图 形的轴对称图形. 对称轴 对称
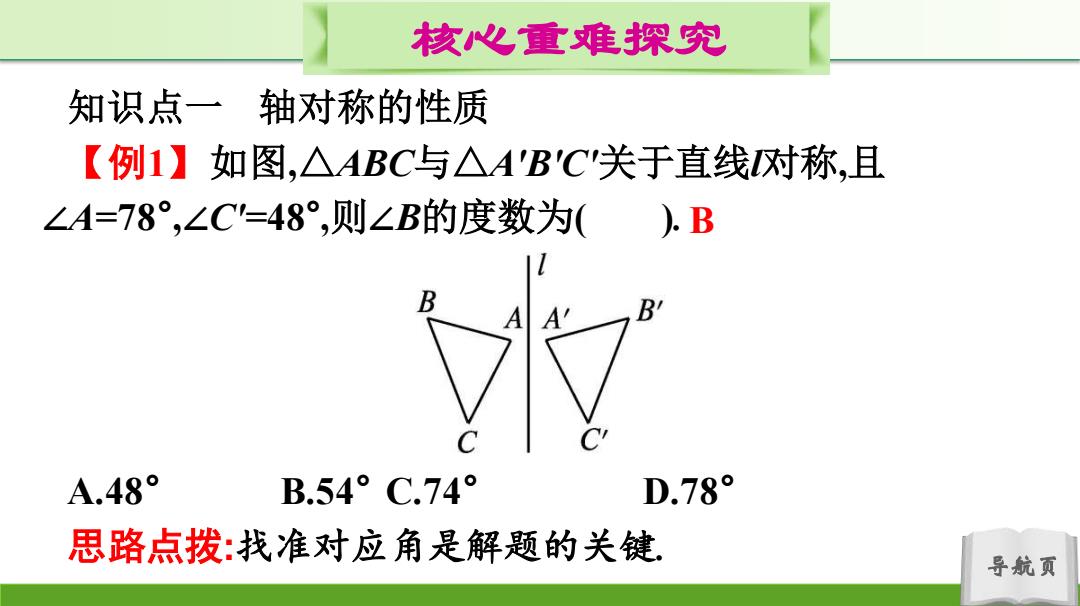
核心重难探究 知识点一轴对称的性质 【例1】如图,△ABC与△A'B'C关于直线对称,且 ∠A=78°,∠C=48°,则∠B的度数为( ).B B A.48° B.54°C.74° D.78° 思路点拨:找准对应角是解题的关键, 导航页
导航页 核心重难探究 知识点一 轴对称的性质 【例1】如图,△ABC与△A'B'C'关于直线l对称,且 ∠A=78° ,∠C'=48° ,则∠B的度数为( ). A.48° B.54° C.74° D.78° 思路点拨:找准对应角是解题的关键. B

核心重难探究 解析:.∠A=78°,∠C=∠C=48°, .∴.∠B=180°-78°-48°=54°. 【方法归纳】 把已知条件转化到同一个三角形中,利用三角形内角和求解 导航页
导航页 核心重难探究 解析:∵∠A=78° ,∠C=∠C'=48° , ∴∠B=180°-78°-48° =54° . 【方法归纳】 把已知条件转化到同一个三角形中,利用三角形内角和求解
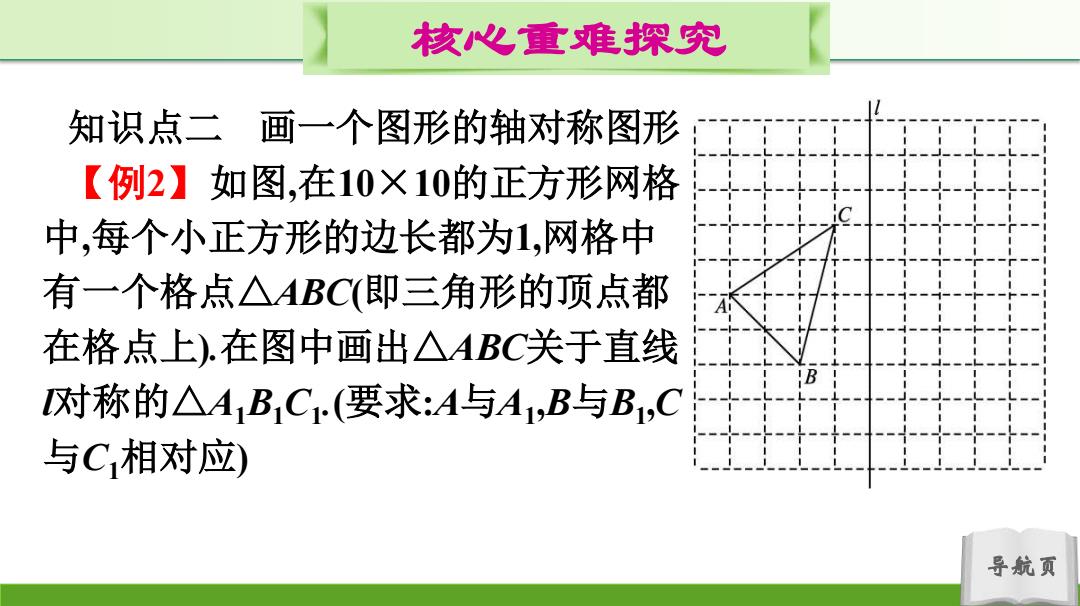
核心重难探究 知识点二画一个图形的轴对称图形 【例2】如图,在10×10的正方形网格 中,每个小正方形的边长都为1,网格中 有一个格点△ABC(即三角形的顶点都 在格点上).在图中画出△ABC关于直线 对称的△A1B1C(要求:A与A1,B与B1,C 与C,相对应) 导航页
导航页 核心重难探究 知识点二 画一个图形的轴对称图形 【例2】如图,在10×10的正方形网格 中,每个小正方形的边长都为1,网格中 有一个格点△ABC(即三角形的顶点都 在格点上).在图中画出△ABC关于直线 l对称的△A1B1C1 .(要求:A与A1 ,B与B1 ,C 与C1相对应)

核心重难探究 思路点拨:画法一:令BM⊥直线I于点M,并延长到B1,使 BM=BM,同样的画法得到A,C的对应点A1,C1,连接相邻两,点 即可得到所求的图形 作法二:根据网格的特点分别找出△ABC各顶点的对称点, 按照原有次序连接即可得出对称三角形 导航页
导航页 核心重难探究 思路点拨:画法一:令BM⊥直线l于点M,并延长到B1 ,使 B1M=BM,同样的画法得到A,C的对应点A1 ,C1 ,连接相邻两点 即可得到所求的图形. 作法二:根据网格的特点分别找出△ABC各顶点的对称点, 按照原有次序连接即可得出对称三角形
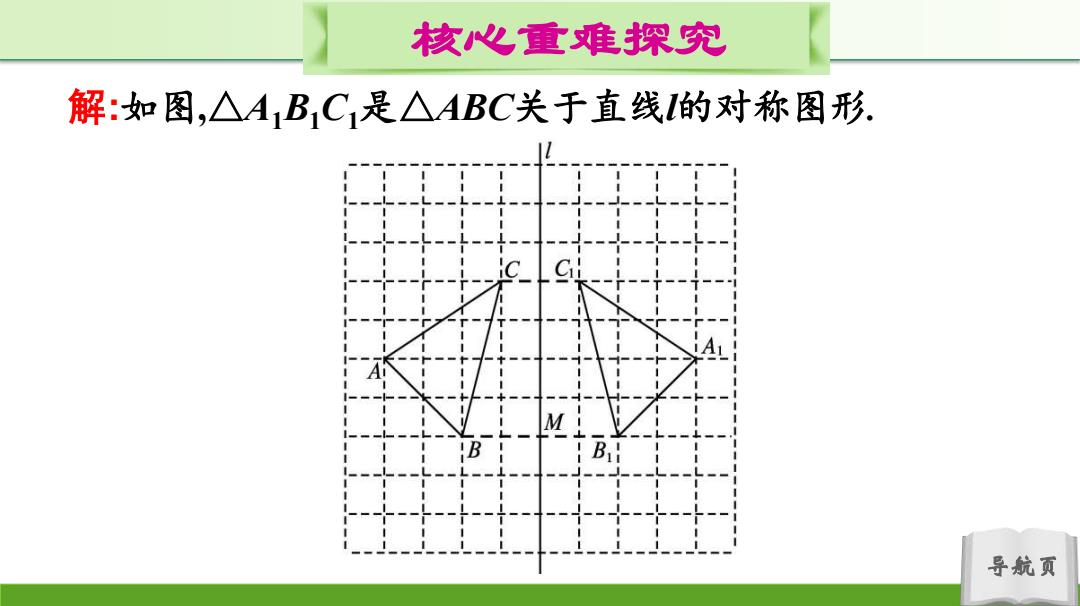
核心重难探究 解:如图,△A1BC1是△ABC关于直线的对称图形. 导航页
导航页 核心重难探究 解:如图,△A1B1C1是△ABC关于直线l的对称图形

核心重难探究 【方法归纳】 网格中利用轴对称画图,应根据题目的要求,结合网格的特 点,尤其是对称轴是网格线(水平方向或竖直方向)时,格点的 对称点也必须是格点 导航页
导航页 核心重难探究 【方法归纳】 网格中利用轴对称画图,应根据题目的要求,结合网格的特 点,尤其是对称轴是网格线(水平方向或竖直方向)时,格点的 对称点也必须是格点