
家庭馆亚 第四章 三角形 5.利用三角形全等测距离
第四章 三角形 5.利用三角形全等测距离

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.当两点可以直接到达时,我们可以直接测量出两点之间的 距离;当两点不可以直接到达时,我们可以通过构造全等三 角形的方法来测量两点之间的距离. 温馨提示 利用三角形全等解决实际问题的步骤:()明确实际问题应 用哪些知识来解决;2)根据实际问题抽象出几何图形;3)结合 图形和题意分析已知条件;(4)找到已知与未知的联系,寻求恰 当的解决途径,并表述清楚 导航页
导航页 基础自主梳理 1.当两点可以直接到达时,我们可以直接测量出两点之间的 距离;当两点不可以直接到达时,我们可以通过构造 三 角形的方法来测量两点之间的距离. 温馨提示 利用三角形全等解决实际问题的步骤:(1)明确实际问题应 用哪些知识来解决;(2)根据实际问题抽象出几何图形;(3)结合 图形和题意分析已知条件;(4)找到已知与未知的联系,寻求恰 当的解决途径,并表述清楚. 全等
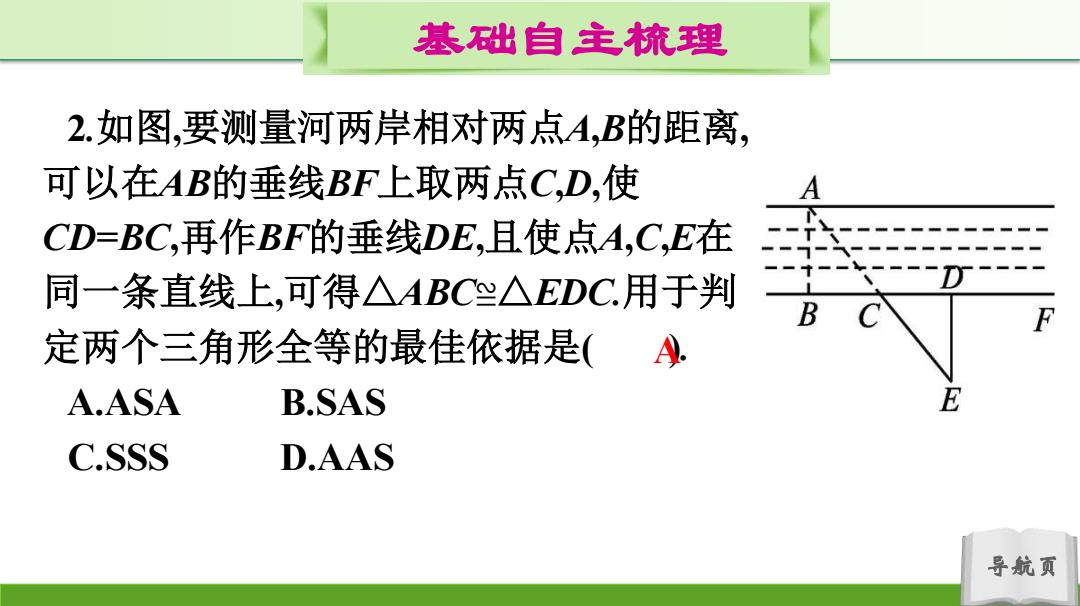
基础自主梳理 2.如图,要测量河两岸相对两点A,B的距离, 可以在AB的垂线BF上取两点C,D,使 A CD=BC,再作BF的垂线DE,且使点A,C,E在 同一条直线上,可得△ABC兰△EDC.用于判 -D B C F 定两个三角形全等的最佳依据是(). A.ASA B.SAS E C.SSS D.AAS 导航页
导航页 基础自主梳理 2.如图,要测量河两岸相对两点A,B的距离, 可以在AB的垂线BF上取两点C,D,使 CD=BC,再作BF的垂线DE,且使点A,C,E在 同一条直线上,可得△ABC≌△EDC.用于判 定两个三角形全等的最佳依据是( ). A.ASA B.SAS C.SSS D.AAS A
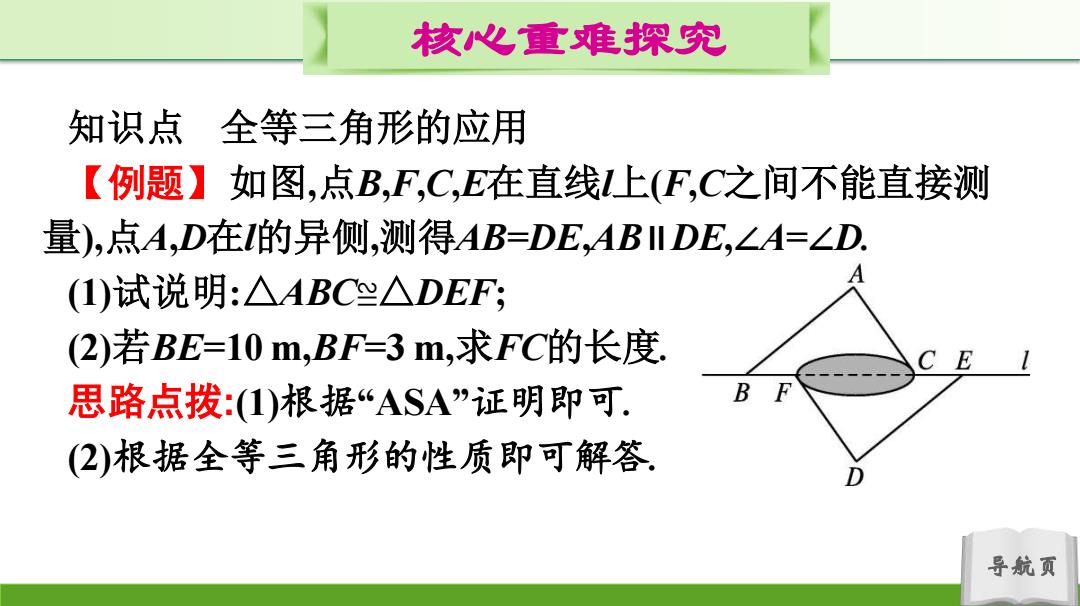
核心重难探究 知识点 全等三角形的应用 【例题】如图,点B,F,C,E在直线1上(F,C之间不能直接测 量),点A,D在I的异侧,测得AB=DE,ABIIDE,∠A=∠D. (1)试说明:△ABC坐△DEF; 2)若BE=10m,BF=3m,求FC的长度. C E 思路点拨:(1)根据“ASA”证明即可. B F (2)根据全等三角形的性质即可解答」 导航页
导航页 核心重难探究 知识点 全等三角形的应用 【例题】如图,点B,F,C,E在直线l上(F,C之间不能直接测 量),点A,D在l的异侧,测得AB=DE,AB∥DE,∠A=∠D. (1)试说明:△ABC≌△DEF; (2)若BE=10 m,BF=3 m,求FC的长度. 思路点拨:(1)根据“ASA”证明即可. (2)根据全等三角形的性质即可解答

核心重难探究 解:(1).ABIDE,∴∠ABC=∠DEF (∠ABC=∠DEF, 在△ABC与△DEF中,}AB=DE, (∠A=∠D, .'.△ABC≌△DEF(ASA) 2).'△ABC≌△DEF,'.BC=EF, .∴.BF+FC=EC+FC,.∴.BF=EC .BE=10m,BF=3m,.∴.FC=10-3-3=4(m. 导航页
导航页 核心重难探究 解:(1)∵AB∥DE,∴∠ABC=∠DEF. 在△ABC 与△DEF 中, ∠𝑨𝑩𝑪 = ∠𝑫𝑬𝑭, 𝑨𝑩 = 𝑫𝑬, ∠𝑨 = ∠𝑫, ∴△ABC≌△DEF(ASA). (2)∵△ABC≌△DEF,∴BC=EF, ∴BF+FC=EC+FC,∴BF=EC. ∵BE=10 m,BF=3 m,∴FC=10-3-3=4(m)

核心重难探究 【方法归纳】 在实际生活中,对于难以实地测量的线段,常常通过两个全 等三角形,转化需要测量的线段到易测量的边上或者已知边 上来,从而求解 导航页
导航页 核心重难探究 【方法归纳】 在实际生活中,对于难以实地测量的线段,常常通过两个全 等三角形,转化需要测量的线段到易测量的边上或者已知边 上来,从而求解
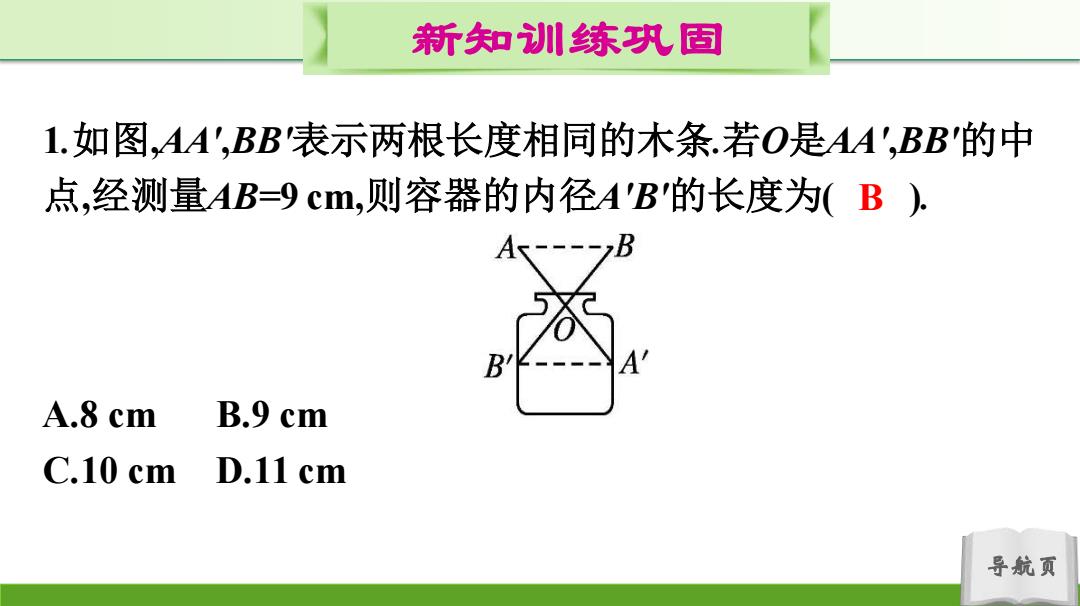
新知训川练巩固 1.如图,AA',BB表示两根长度相同的木条.若O是AA',BB的中 点,经测量AB=9cm,则容器的内径A'B的长度为(B), A--- B B A.8 cm B.9 cm C.10cm】 D.11 cm 导航页
导航页 新知训练巩固 1.如图,AA',BB'表示两根长度相同的木条.若O是AA',BB'的中 点,经测量AB=9 cm,则容器的内径A'B'的长度为( ). A.8 cm B.9 cm C.10 cm D.11 cm B
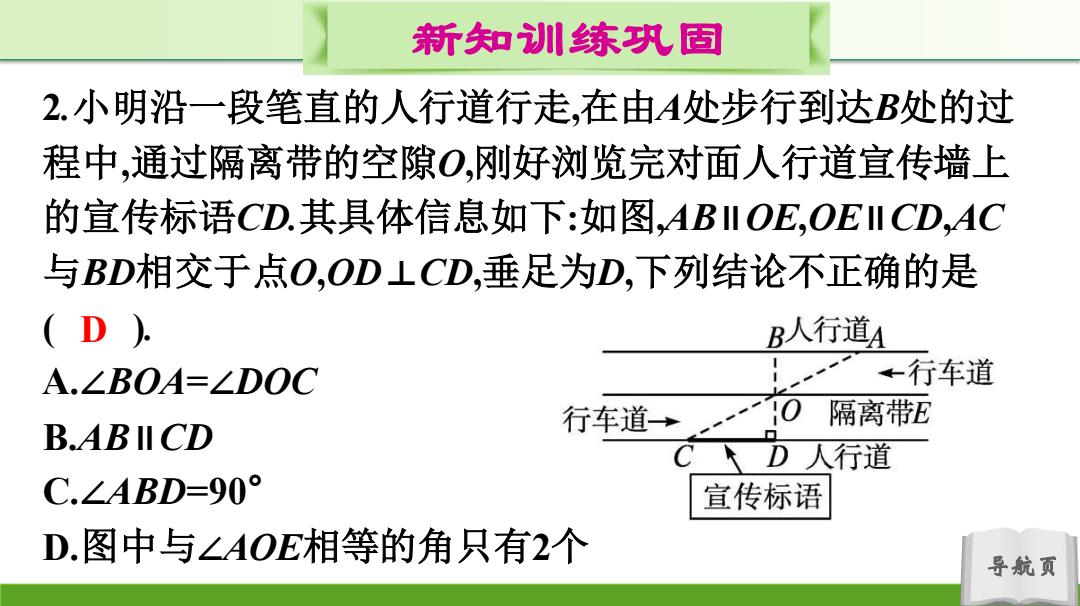
新知训练巩固 2.小明沿一段笔直的人行道行走,在由A处步行到达B处的过 程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上 的宣传标语CD.其具体信息如下:如图,ABIIOE,OEII CD,AC 与BD相交于点O,OD⊥CD,垂足为D,下列结论不正确的是 (D) B人行道A A.∠BOA=∠DOC ←行车道 行车道→0 隔离带E B.AB IICD ,个D人行道 C.∠ABD=90° 宣传标语 D.图中与∠AOE相等的角只有2个 导航页
导航页 新知训练巩固 2.小明沿一段笔直的人行道行走,在由A处步行到达B处的过 程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上 的宣传标语CD.其具体信息如下:如图,AB∥OE,OE∥CD,AC 与BD相交于点O,OD⊥CD,垂足为D,下列结论不正确的是 ( ). A.∠BOA=∠DOC B.AB∥CD C.∠ABD=90° D.图中与∠AOE相等的角只有2个 D
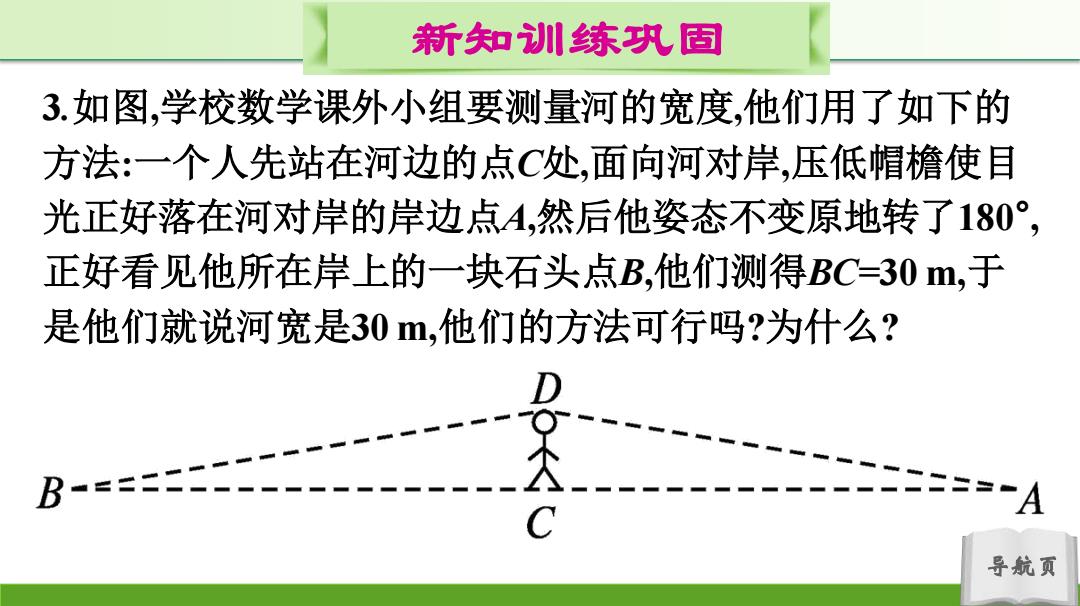
新知训练巩固 3.如图,学校数学课外小组要测量河的宽度,他们用了如下的 方法:一个人先站在河边的点C处,面向河对岸,压低帽檐使目 光正好落在河对岸的岸边点A,然后他姿态不变原地转了180°, 正好看见他所在岸上的一块石头点B,他们测得BC=30m,于 是他们就说河宽是30,他们的方法可行吗?为什么? B==二二 “A 导航页
导航页 新知训练巩固 3.如图,学校数学课外小组要测量河的宽度,他们用了如下的 方法:一个人先站在河边的点C处,面向河对岸,压低帽檐使目 光正好落在河对岸的岸边点A,然后他姿态不变原地转了180° , 正好看见他所在岸上的一块石头点B,他们测得BC=30 m,于 是他们就说河宽是30 m,他们的方法可行吗?为什么?