
家庭亚 3.探索三角形全等的条件 第3课时 边角边
3.探索三角形全等的条件 第3课时 边角边

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.两边及其 夹 角分别相等的两个三角形全等,简写 成边角边”或“ SAS 99 温馨提示 必须是两边及其夹角分别相等才成立.若是其他角相等,两 个三角形不一定全等 导航页
导航页 基础自主梳理 1.两边及其 角分别相等的两个三角形全等,简写 成“ ”或“ ” . 温馨提示 必须是两边及其夹角分别相等才成立.若是其他角相等,两 个三角形不一定全等. 夹 边角边 SAS
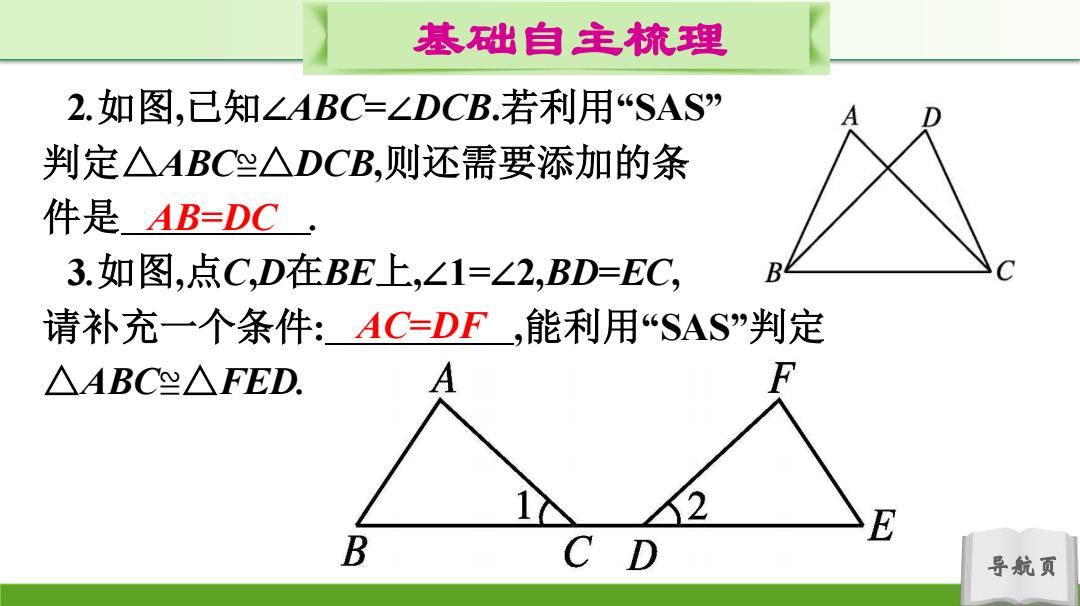
基础自主梳理 2.如图,已知∠ABC=∠DCB.若利用“SAS” 判定△ABC烂△DCB,则还需要添加的条 件是AB=DC 3.如图,点C,D在BE上,∠1=∠2,BD=EC, B 请补充一个条件:AC=DF,能利用SAS”判定 △ABCY△FED. E B 导航页
导航页 基础自主梳理 2.如图,已知∠ABC=∠DCB.若利用“SAS” 判定△ABC≌△DCB,则还需要添加的条 件是 . 3.如图,点C,D在BE上,∠1=∠2,BD=EC, 请补充一个条件: ,能利用“SAS”判定 △ABC≌△FED. AB=DC AC=DF
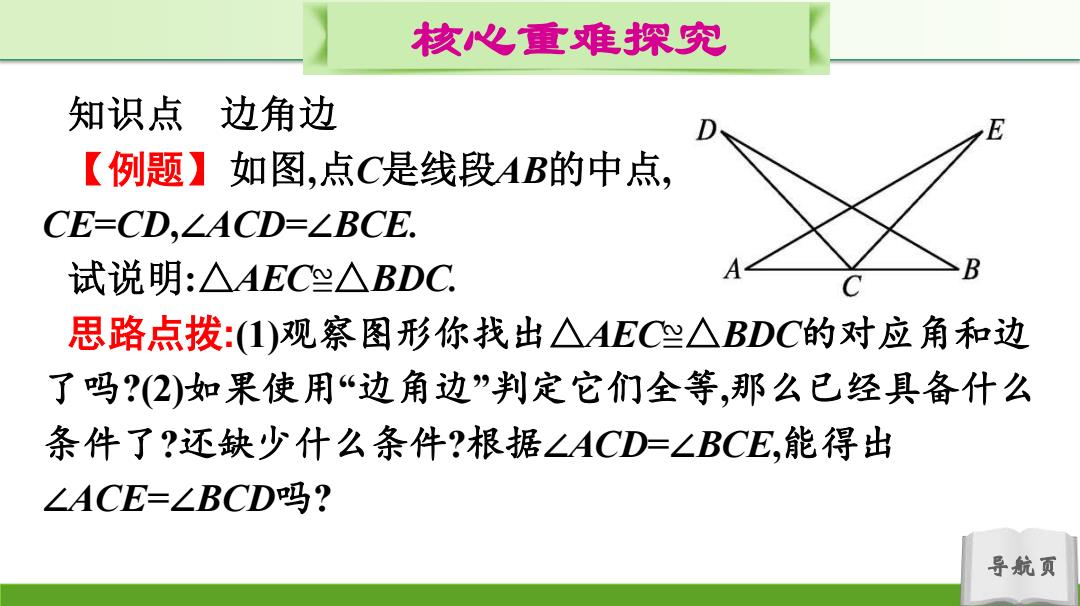
核心重难探究 知识点 边角边 【例题】如图,点C是线段AB的中点, CE=CD,∠ACD=∠BCE. 试说明:△AEC兰△BDC A D 思路点拨:(1)观察图形你找出△AEC兰△BDC的对应角和边 了吗?(2)如果使用“边角边”判定它们全等,那么已经具备什么 条件了?还缺少什么条件?根据∠ACD=∠BCE,能得出 ∠ACE=∠BCD吗? 导航页
导航页 核心重难探究 知识点 边角边 【例题】如图,点C是线段AB的中点, CE=CD,∠ACD=∠BCE. 试说明:△AEC≌△BDC. 思路点拨:(1)观察图形你找出△AEC≌△BDC的对应角和边 了吗?(2)如果使用“边角边”判定它们全等,那么已经具备什么 条件了?还缺少什么条件?根据∠ACD=∠BCE,能得出 ∠ACE=∠BCD吗?

核心重难探究 解:点C是线段AB的中点, .∴AC=BC .∠ACD=∠BCE, .'.∠ACD+∠DCE=∠BCE+∠DCE, 即∠ACE=∠BCD. AC=BC, 在△AEC和△BDC中,{LACE=∠BCD, CE=CD, .∴.△AEC≌△BDC(SAS) 导航页
导航页 核心重难探究 解:∵点C是线段AB的中点, ∴AC=BC. ∵∠ACD=∠BCE, ∴∠ACD+∠DCE=∠BCE+∠DCE, 即∠ACE=∠BCD. 在△AEC 和△BDC 中, 𝑨𝑪 = 𝑩𝑪, ∠𝑨𝑪𝑬 = ∠𝑩𝑪𝑫, 𝑪𝑬 = 𝑪𝑫, ∴△AEC≌△BDC(SAS)

核心重难探究 【方法归纳】 至此已经学习了判定两个三角形全等的一般方法有:“SSS” “SAS“ASA”“AAS”,选择什么样的方法应灵活运用.当已经 具备两条边相等时,有两种方法:若考虑使用“SAS,则设法说 明夹角相等;若考虑使用“SSS”,则设法说明第三边相等即可. 导航页
导航页 核心重难探究 【方法归纳】 至此已经学习了判定两个三角形全等的一般方法有:“SSS” “SAS”“ASA”“AAS”,选择什么样的方法应灵活运用.当已经 具备两条边相等时,有两种方法:若考虑使用“SAS”,则设法说 明夹角相等;若考虑使用“SSS”,则设法说明第三边相等即可
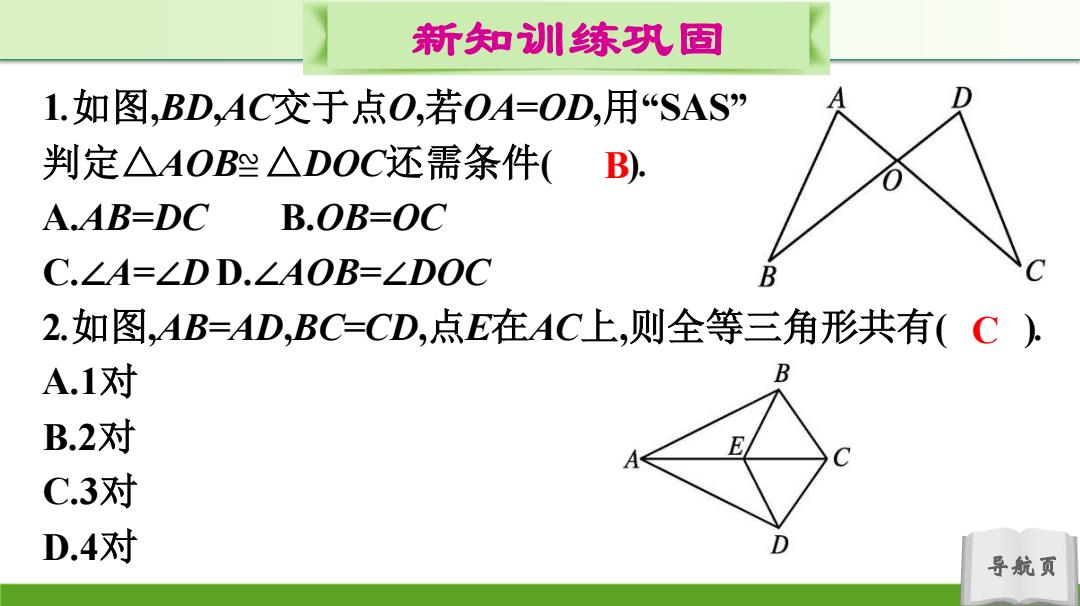
新知训练巩固 1.如图,BD,AC交于点O,若OA=OD,用“SAS” 判定△AOB兴△DOC还需条件(B). A.AB-DC B.OB-OC C.∠A=∠DD.∠AOB=∠DOC B 2.如图,AB=AD,BC=CD,点E在AC上,则全等三角形共有(C) A.1对 B.2对 C.3对 D.4对 导航页
导航页 新知训练巩固 1.如图,BD,AC交于点O,若OA=OD,用“SAS” 判定△AOB≌△DOC还需条件( ). A.AB=DC B.OB=OC C.∠A=∠D D.∠AOB=∠DOC 2.如图,AB=AD,BC=CD,点E在AC上,则全等三角形共有( ). A.1对 B.2对 C.3对 D.4对 B C
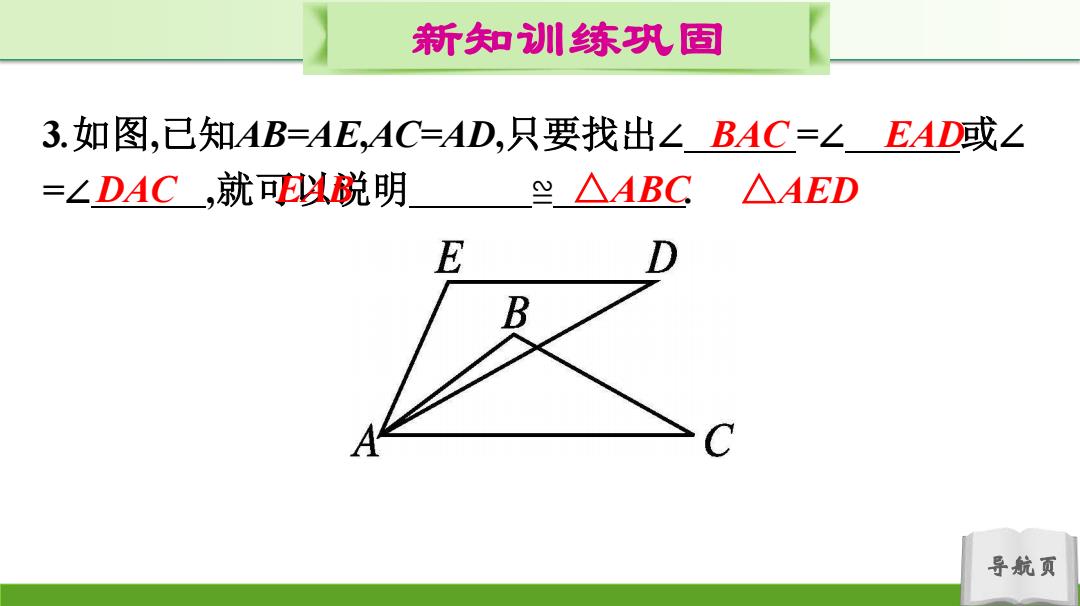
新知训川练巩固 3.如图,已知AB=AE,AC=AD,只要找出∠BAC=∠EAD或∠ =∠DAC,就可以税明 Y△ABC△AED E B A C 导航页
导航页 新知训练巩固 3.如图,已知AB=AE,AC=AD,只要找出∠ =∠ 或∠ =∠ ,就可以说明 ≌ . BAC EAD DAC EAB △ABC △AED
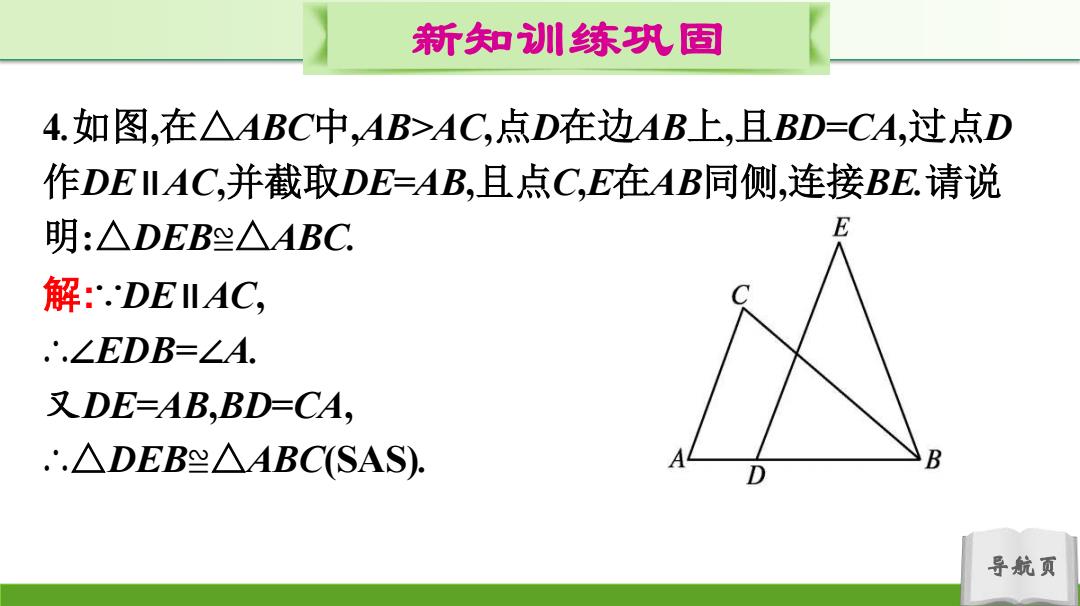
新知训练巩固 4.如图,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D 作DEIAC,并截取DE=AB,且点C,E在AB同侧,连接BE.请说 明:△DEB≈△ABC 解:DEILAC, .∴.∠EDB=∠A. 又DE=AB,BD=CA, '.△DEB≌△ABC(SAS) 导航页
导航页 新知训练巩固 4.如图,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D 作DE∥AC,并截取DE=AB,且点C,E在AB同侧,连接BE.请说 明:△DEB≌△ABC. 解:∵DE∥AC, ∴∠EDB=∠A. 又DE=AB,BD=CA, ∴△DEB≌△ABC(SAS)