
家庭復鸿 第六章 概率初步 2.频率的稳定性
第六章 概率初步 2.频率的稳定性

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1频率的稳定性: m (1)在n次重复试验中,事件A发生了m次,则比值 五称 为事件A发生的频率 (2)无论是掷质地均匀的硬币还是掷图钉,在试验次数很大 时正面朝上(针尖朝上)的频率都会在一个常数附近摆动,这就 是频率的稳定性 2.已知事件A发生的频数是4,试验总次数为20,则事件A发生 的频率是 0.2 导航页
导航页 基础自主梳理 1.频率的稳定性: (1)在n次重复试验中,事件A发生了m次,则比值 称 为事件A发生的频率. (2)无论是掷质地均匀的硬币还是掷图钉,在试验次数很大 时正面朝上(针尖朝上)的频率都会在一个常数附近摆动,这就 是频率的 . 2.已知事件A发生的频数是4,试验总次数为20,则事件A发生 的频率是 . 𝒎 𝒏 稳定性 0.2

基础自主梳理 3.概率的意义: 由于事件A发生的频率,表示该事件发生的频繁程度,频率越 大,事件A发生越频繁,这就意味着事件A发生的可能性也越大, 因而,我们就用这个常数来表示事件A发生的可能性的大小 我们把刻画事件A发生的可能性大小的数值,称为事件A发生 的概率,记为P(A) 导航页
导航页 基础自主梳理 3.概率的意义: 由于事件A发生的频率,表示该事件发生的频繁程度,频率越 大,事件A发生越频繁,这就意味着事件A发生的可能性也越大, 因而,我们就用这个常数来表示事件A发生的可能性的大小. 我们把刻画事件A发生的可能性大小的数值,称为事件A发生 的 概率 ,记为P(A)

基础自主梳理 4.(1)一般地,大量重复的试验中,我们常用随机事件A发生的 频率 来估计事件A发生的概率 (2)必然事件发生的概率为1 ;不可能事件发生的 概率为0 ;随机事件A发生的概率P(A)是0与1之间的 一个常数 导航页
导航页 基础自主梳理 4.(1)一般地,大量重复的试验中,我们常用随机事件A发生的 来估计事件A发生的概率. (2)必然事件发生的概率为 ;不可能事件发生的 概率为 ;随机事件A发生的概率P(A)是0与1之间的 一个常数. 频率 1 0
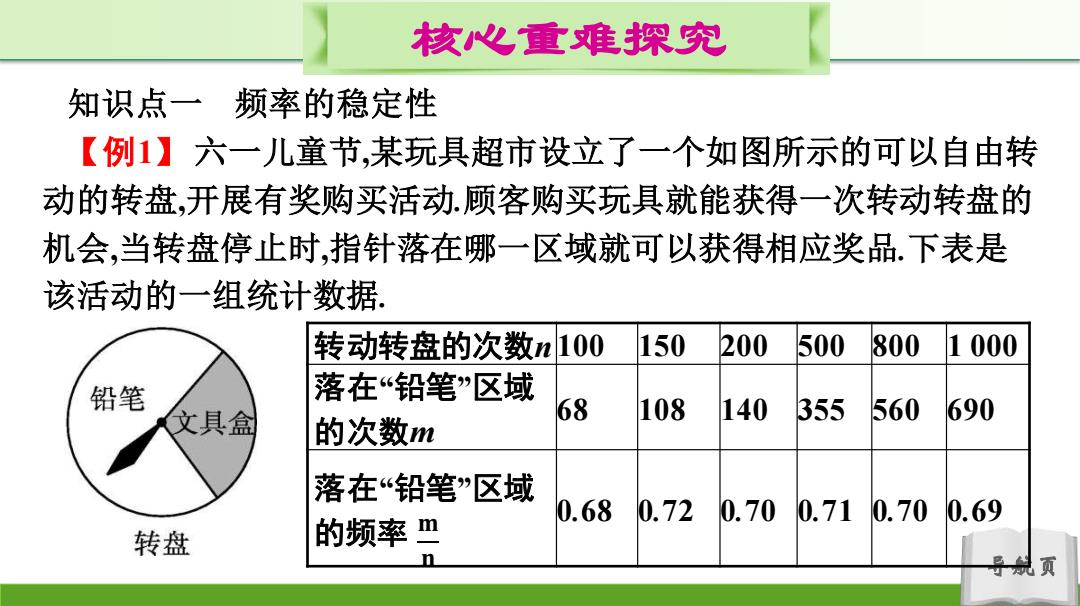
核心重难探究 知识点一频率的稳定性 【例1】六一儿童节,某玩具超市设立了一个如图所示的可以自由转 动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的 机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是 该活动的一组统计数据。 转动转盘的次数n100 150 200 500 800 1000 铅笔 落在“铅笔”区域 文具盒 68 108 140 355 560 690 的次数m 落在“铅笔区域 0.68 0.72 0.700.71 0.70 0.69 转盘 的频率” n 导就页
导航页 核心重难探究 知识点一 频率的稳定性 【例1】 六一儿童节,某玩具超市设立了一个如图所示的可以自由转 动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的 机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是 该活动的一组统计数据. 转动转盘的次数n 100 150 200 500 800 1 000 落在“铅笔”区域 的次数m 68 108 140 355 560 690 落在“铅笔”区域 的频率 𝐦 0.68 0.72 0.70 0.71 0.70 0.69 𝐧

核心重难探究 下列说法不正确的是(D), A.当很大时,估计指针落在“铅笔”区域的频率大约是0.70 B.假如你去转动转盘一次,获得铅笔的可能性大约是0.70 C.如果转动转盘2000次,那么指针落在“文具盒”区域的次 数大约有600次 D.转动转盘10次,一定有3次获得文具盒 思路点拨:理解频率与概率的联系与区别是解题的关键, 导航页
导航页 核心重难探究 下列说法不正确的是( ). A.当n很大时,估计指针落在“铅笔”区域的频率大约是0.70 B.假如你去转动转盘一次,获得铅笔的可能性大约是0.70 C.如果转动转盘2 000次,那么指针落在“文具盒”区域的次 数大约有600次 D.转动转盘10次,一定有3次获得文具盒 思路点拨:理解频率与概率的联系与区别是解题的关键. D

核心重难探究 解析:A.频率稳定在0.7左右,故指针落在“铅笔”区域的频率 大约是0.70; B.由A可知转动转盘一次,获得铅笔的可能性大约是0.70; C.指针落在“文具盒”区域的可能性约为0.30,转动转盘2000 次,指针落在“文具盒”区域的次数大约为2000X0.3=600; D.随机事件,结果不确定 【方法归纳】 正确理解试验得出的某事件发生的频率是关键,只有试验次 数足够大时,频率才具有稳定性 导航页
导航页 核心重难探究 【方法归纳】 正确理解试验得出的某事件发生的频率是关键,只有试验次 数足够大时,频率才具有稳定性. 解析:A.频率稳定在0.7左右,故指针落在“铅笔”区域的频率 大约是0.70; B.由A可知转动转盘一次,获得铅笔的可能性大约是0.70; C.指针落在“文具盒”区域的可能性约为0.30,转动转盘2 000 次,指针落在“文具盒”区域的次数大约为2 000×0.3=600; D.随机事件,结果不确定

核心重难探究 知识点二用频率估计概率 【例2】在一个不透明的布袋中装有红色、白色玻璃球共 40个,这些玻璃球除颜色外其他完全相同小明通过多次摸球 试验后发现,其中摸到红色球的频率稳定在15%左右,则口袋 中红色球可能有(B). A.4个 B.6个 C.34个 D.36个 导航页
导航页 核心重难探究 知识点二 用频率估计概率 【例2】在一个不透明的布袋中装有红色、白色玻璃球共 40个,这些玻璃球除颜色外其他完全相同.小明通过多次摸球 试验后发现,其中摸到红色球的频率稳定在15%左右,则口袋 中红色球可能有( ). A.4个 B.6个 C.34个 D.36个 B

核心重难探究 解析:摸到红色球的频率稳定在15%左右, .摸到红色球的概率约为15%, 故红色球的个数约为40X15%=6. 【方法归纳】 解答这类问题,先把概率作为频率,再根据频数=数据总数× 频(概)率计算即可. 导航页
导航页 核心重难探究 【方法归纳】 解答这类问题,先把概率作为频率,再根据频数=数据总数× 频(概)率计算即可. 解析:∵摸到红色球的频率稳定在15%左右, ∴摸到红色球的概率约为15%, 故红色球的个数约为40×15%=6