
家庭侯雪 3.简单的轴对称图形 第1课时等腰三角形
3.简单的轴对称图形 第1课时 等腰三角形

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.等腰三角形的性质: (1)等腰三角形是轴对称图形; (2)等腰三角形顶角的平分线、底边上的 中线、底 边上的高 重合(也称“三线合一),它们所在的直线都 是等腰三角形的对称轴; (3)等腰三角形的两个底角相等 2.若等腰三角形的一个底角为50°,则它的顶角的度数 为80° 导航页
导航页 基础自主梳理 1.等腰三角形的性质: (1)等腰三角形是轴对称图形; (2)等腰三角形顶角的平分线、底边上的 线、底 边上的 重合(也称“三线合一”),它们所在的直线都 是等腰三角形的对称轴; (3)等腰三角形的两个底角 . 2.若等腰三角形的一个底角为50° ,则它的顶角的度数 为 . 中 高 相等 80°
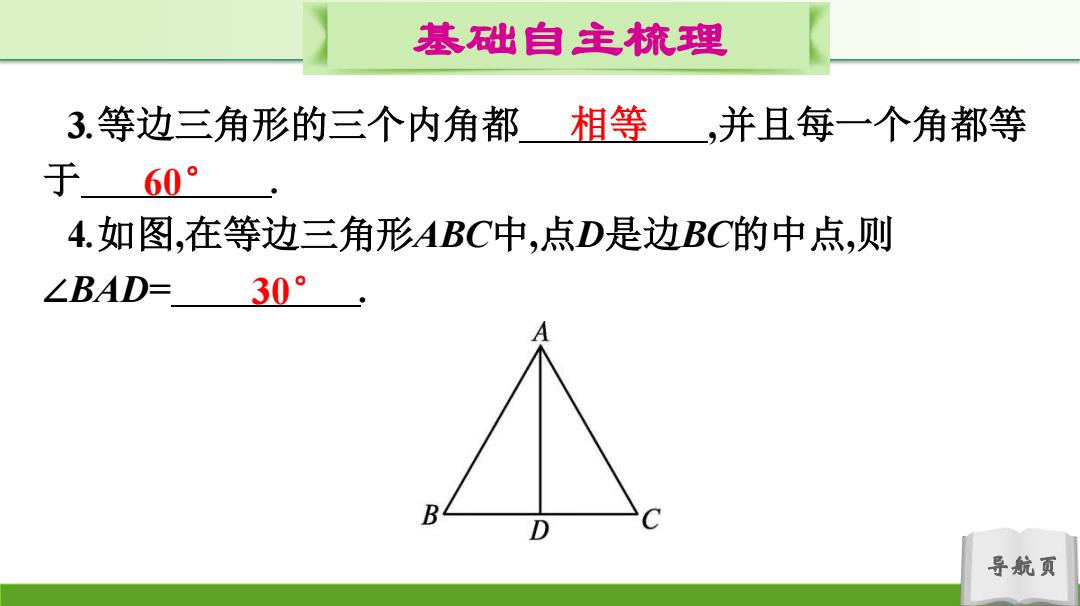
基础自主梳理 3.等边三角形的三个内角都相等,并且每一个角都等 于60° 4.如图,在等边三角形ABC中,点D是边BC的中点,则 ∠BAD= 30° B D 导航页
导航页 基础自主梳理 3.等边三角形的三个内角都 ,并且每一个角都等 于 . 4.如图,在等边三角形ABC中,点D是边BC的中点,则 ∠BAD= . 相等 60° 30°
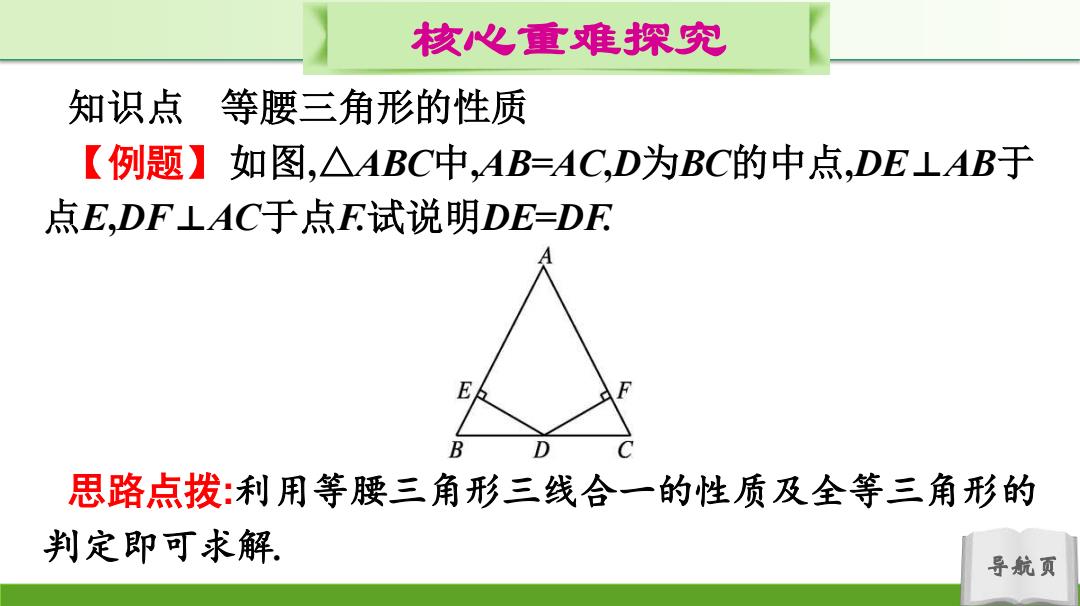
核心重难探究 知识点 等腰三角形的性质 【例题】如图,△ABC中,AB=AC,D为BC的中点,DE LAB于 点E,DF LAC于点R试说明DE=DR 思路点拨:利用等腰三角形三线合一的性质及全等三角形的 判定即可求解 导航页
导航页 核心重难探究 知识点 等腰三角形的性质 【例题】如图,△ABC中,AB=AC,D为BC的中点,DE⊥AB于 点E,DF⊥AC于点F.试说明DE=DF. 思路点拨:利用等腰三角形三线合一的性质及全等三角形的 判定即可求解

核心重难探究 解:连接AD(图略), D为BC的中点,AB=AC, .'AD平分∠BAC,即∠EAD=∠FAD 又DE⊥AB,DF⊥AC,.∴.∠AED=∠AFD 又AD=AD, ∴.△AED≌△AFD.∴.DE=DF 导航页
导航页 核心重难探究 解:连接AD(图略). ∵D为BC的中点,AB=AC, ∴AD平分∠BAC,即∠EAD=∠FAD. 又DE⊥AB,DF⊥AC,∴∠AED=∠AFD. 又AD=AD, ∴△AED≌△AFD.∴DE=DF

核心重难探究 【方法归纳】 等腰三角形底边上的中线、底边上的高、顶角的平分线 “三线合一”,这个性质应用十分广泛.与等腰三角形有关的问 题,作底边上的高(或底边上的中线或顶角的平分线)为辅助线, 常常会有意想不到的效果 导航页
导航页 核心重难探究 【方法归纳】 等腰三角形底边上的中线、底边上的高、顶角的平分线 “三线合一”,这个性质应用十分广泛.与等腰三角形有关的问 题,作底边上的高(或底边上的中线或顶角的平分线)为辅助线, 常常会有意想不到的效果

新知训练织固 1.已知等腰三角形的一个内角为70°,则另外两个内角的度数 分别是(D), A.55°,55°B.70°,40°或70°,55° C.70°,40°D.55°,55°或70°,40° 导航页
导航页 新知训练巩固 1.已知等腰三角形的一个内角为70° ,则另外两个内角的度数 分别是( ). A.55°,55° B.70°,40°或70°,55° C.70°,40° D.55°,55°或70°,40° D

新知训练巩固 2.如图,在△ABC中,AD⊥BC,AB=AC, ∠BAD=30°,且AD=AE,则∠EDC等于( A.10° B.12.5° C.15° D.20° B D 3.已知等腰三角形两边的长分别为3和7,则此等腰三角形的周 长为(B) A.13 B.17 C.13或17 D.13或10 4.在△ABC中,AB=AC,∠A=40°,则∠B= 70° 导航页
导航页 新知训练巩固 2.如图,在△ABC中,AD⊥BC,AB=AC, ∠BAD=30° ,且AD=AE,则∠EDC等于( ). A.10° B.12.5° C.15° D.20° 3.已知等腰三角形两边的长分别为3和7,则此等腰三角形的周 长为( ). A.13 B.17 C.13或17 D.13或10 4.在△ABC中,AB=AC,∠A=40° ,则∠B= . C B 70°

素能演练提升 1.如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于 B ) B D C A.10 B.5 C.4 D.3 导航页
导航页 素能演练提升 1.如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于 ( ). A.10 B.5 C.4 D.3 B