
第七章 群体遗传学 (population genetics)
第七章 群体遗传学 (population genetics)

群体(population)孟德尔式群体(Mendelian population) 指生活在某一地区的、能够相互交配并能产生具有生殖能力后代的个体群。 群体遗传学(population genetics)研究群体的遗传结构及其变化规律 的科学,主要是应用数学的思维和方法研究和探讨群体的基因频率、基因型频率及其 和某些因素的关系。 医学群体遗传学(medical population genetics) 基因库(gene pool)一个群体所具有的全部遗传信息 第一节 群体中的遗传平衡 一、基因频率和基因型频率 基因频率(gene frequency) 某一基因的数量所有等位基因数量(例如) 基因型频率(genotype frequency): 某一基因型个体数/总个体数 (例如)D+H+R=1
群体 (population )孟德尔式群体 (Mendelian population ) 指生活在某一地区的、能够相互交配并能产生具有生殖能力后代的个体群。 群体遗传学 (population genetics)研究群体的遗传结构及其变化规律 的科学,主要是应用数学的思维和方法研究和探讨群体的基因频率、基因型频率及其 和某些因素的关系。 医学群体遗传学 (medical population genetics) 基因库 (gene pool)一个群体所具有的全部遗传信息 第一节 群体中的遗传平衡 一、基因频率和基因型频率 基因频率(gene frequency): 某一基因的数量/所有等位基因数量 (例如) 基因型频率(genotype frequency): 某一基因型个体数/总个体数 (例如) D + H + R = 1

MN血型一共显性遗传, 基因定位一4q 基因型 表型 个体数 M/M M血型 747×0.312=233 M/N MN血型 747×0.515=385 N/N N血型 747×0.173=129 总计 747 一对等位基因决定一个表型性状 M基因的频率:p=(233×2+385)/(747X2) =(233/747)+1/2(385/747) MM+1/2 MN =0.57 公式:p=D+1/2H N基因的频率:q=1-0.57=0.43 9=R+1/2H
MN血型——共显性遗传,基因定位——4q 基因型 表型 个体数 M / M M血型 747× 0.312=233 M / N MN血型 747× 0.515 =385 N / N N血型 747 ×0.173 =129 总计 747 一对等位基因决定一个表型性状 M基因的频率: p =(233 ×2+385)/(747×2) =(233/747) +1/2 (385/747) = MM + 1/2 MN =0.57 N基因的频率: q =1-0.57 =0.43 公式:p =D +1/2H q =R +1/2H
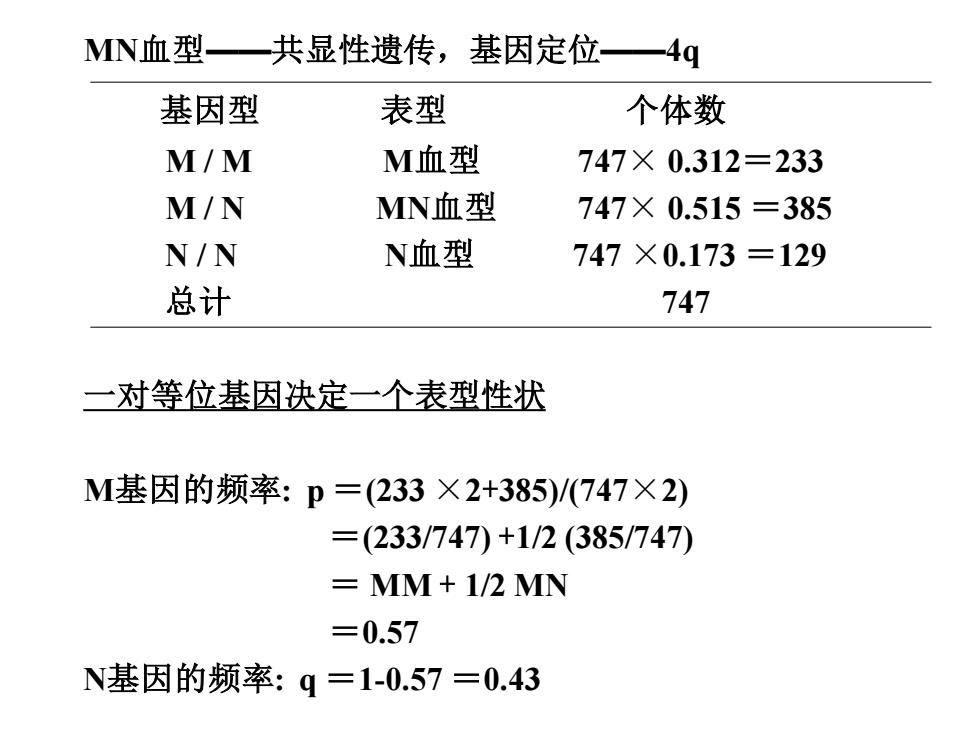
MN血型一共显性遗传, 基因定位一4g 基因型 表型 个体数 M/M M血型 747×0.312=233 M/N MN血型 747×0.515=385 N/N N血型 747×0.173=129 总计 747 一对等位基因决定一个表型性状 M基因的频率:p=(233×2+385)/(747×2) =(233/747)+1/2(385/747) MM+1/2 MN =0.57 N基因的频率:q=1-0.57=0.43
MN血型——共显性遗传,基因定位——4q 基因型 表型 个体数 M / M M血型 747× 0.312=233 M / N MN血型 747× 0.515 =385 N / N N血型 747 ×0.173 =129 总计 747 一对等位基因决定一个表型性状 M基因的频率: p =(233 ×2+385)/(747×2) =(233/747) +1/2 (385/747) = MM + 1/2 MN =0.57 N基因的频率: q =1-0.57 =0.43

二、遗传平衡定律(law of genetic equilibrium,1908) Hardy-Veinberg定律:在一定条件下,群体中的基因频率 和基因型频率在世代传递中保持代代不变。 条件:1、群体很大;2、随机婚配;3、没有突变发生; 4、没有选择;5、无大规模的个体迁移。 遗传平衡公式:假设一对等位基因A和a,基因A的频率为p, 基因a的频率为q, p+q=1,(p+q)2=1,p2+2pq+q2=1 在一个遗传平衡的群体里: p2—AA;q2—aa;2pq—Aa 即AA:Aa:aa=p2:2pq:q2
二、遗传平衡定律(law of genetic equilibrium,1908) Hardy-Weinberg定律:在一定条件下,群体中的基因频率 和基因型频率在世代传递中保持代代不变。 条件:1、群体很大;2、随机婚配;3、没有突变发生; 4、没有选择;5、无大规模的个体迁移。 遗传平衡公式:假设一对等位基因A和 a,基因A的频率为p, 基因a的频率为q, p + q =1,( p + q )2=1, p 2+2pq +q 2=1 在一个遗传平衡的群体里: p 2——AA; q 2——aa;2pq——Aa 即 AA:Aa:aa = p 2:2pq :q 2

·假设有一个100万人口的群体,某一对等位基因A和 a,AA个体有60万人,Aa个体20万人,aa个体也有20 万人。 。 基因型AA、Aa和aa的频率: ● D=60/100=0.6 H=20/100=0.2 ● R=20/100=0.2 ·群体基因A和a的基因频率: 。p=D+1/2H=0.6+0.2/2=0.7 9=R+1/2H=0.2+0.2/2=0.3
• 假设有一个100万人口的群体,某一对等 位基因A和 a,AA个体有60万人,Aa个体20万人,aa个体也有20 万人。 • 基因型AA、Aa和aa的频率: • D =60/100=0.6 • H =20/100=0.2 • R =20/100=0.2 • 群体基因A和a的基因频率: • p =D +1/2H =0.6+0.2/2=0.7 • q =R +1/2H =0.2+0.2/2=0.3

亲本精卵随机结合子一代基因型及其频率 精 子 ++ Ap=0.7 aq=0.3 卵Ap-0.7AAp2=0.49 Aa pq=0.21 子aq=0.3 Aa pq=0.21 aag2=0.09
亲本精卵随机结合子一代基因型及其频率 精 子 A p=0.7 a q=0.3 卵 子 AA p 2=0.49 Aa pq =0.21 Aa pq =0.21 aa q 2 =0.09 A p=0.7 a q=0.3

·子一代基因A的频率 p=D+1/2H=0.49+1/2(0.21+0.21) =0.7 q=R+1/2H=0.09+1/2(0.21+0.21) =0.3
• 子一代基因A的频率 p = D +1/2H =0.49+1/2(0.21+0.21) =0.7 q =R +1/2H =0.09+1/2(0.21+0.21) =0.3

子一代精卵随机结合子二代基因型及其频率 精 子 Ap=0.7 aq=0.3 卵Ap=0.7 AAp2=0.49 Aa pq=0.21 子aq-0.3 Aa pq=0.21 aaq2=0.09
子一代精卵随机结合子二代基因型及其频率 精 子 A p=0.7 a q=0.3 卵 子 AA p 2=0.49 Aa pq =0.21 Aa pq =0.21 aa q 2 =0.09 A p=0.7 a q=0.3

三、遗传平衡定律的应用 (一)遗传平衡群体的判定 例题:在一个群体中,AA的频率为0.36,Aa的频率为0.48, aa的频率为0.16,判定此群体是否是遗传平衡群体。 A基因频率:p=D+1/2H=0.36+0.48/2=0.6 a基因频率:q=R+1/2H=1-0.6=0.4 根据遗传平衡公式推算理论值: AA的频率p2=0.62=0.36 Aa的频率2pq=2×0.6×0.4=0.48 aa的频率q2=0.42=0.16 基因型频率的实际值和平衡状态时的理论值完全一样。 结论:该群体是遗传平衡群体
三、遗传平衡定律的应用 (一)遗传平衡群体的判定 例题:在一个群体中,AA的频率为0.36, Aa的频率为0.48, aa的频率为0.16,判定此群体是否是遗传平衡群体。 A基因频率:p =D+1/2H=0.36 +0.48/2 =0.6 a基因频率: q =R+1/2H=1-0.6 =0.4 根据遗传平衡公式推算理论值: AA的频率 p 2=0.6 2=0.36 Aa的频率 2pq =2 ×0.6 ×0.4=0.48 aa的频率 q 2=0.42=0.16 基因型频率的实际值和平衡状态时的理论值完全一样。 结论:该群体是遗传平衡群体