
投资学 第十三章投资组合与证 券定价原理 金融与贸易学院
第十三章 投资组合与证 券定价原理 投资学—— 金融与贸易学院

课程目标 认识投资组合的概念与含义 从定性与定量相结合的角度 了解投资组合的收益与风险 关系 3 掌握资本资产定价模型
课程目标 1 认识投资组合的概念与含义 2 从定性与定量相结合的角度 了解投资组合的收益与风险 关系 3 掌握资本资产定价模型

目录 ontents 证券投资组合管理 2 资本资产定价模型
证券投资组合管理 资本资产定价模型 1 2

713.1证券投资组合管理
13.1 证券投资组合管理

13.1证券投资组合管理 13.1.1投资组合的含义 投资组合是一个总体概念,这个总体由若干个个体 组成,而各个个体在种类或收益上可能各不相同。 投资组合有一个广泛的含义,当所有个体均是投资 项目时,则称为“投资项目组合”;如果只是证券 则称为“证券组合”;再更细分,若个体是债券或 股票,则分别称为“债券组合”或“股票组合”。 ● 本节主要研究股票组合。 投资组合的目的是规避风险,不把所有的鸡蛋都放 在一个篮子里
13.1.1 投资组合的含义 13.1 证券投资组合管理 ⚫ 投资组合是一个总体概念,这个总体由若干个个体 组成,而各个个体在种类或收益上可能各不相同。 ⚫ 投资组合有一个广泛的含义,当所有个体均是投资 项目时,则称为“投资项目组合”;如果只是证券 则称为“证券组合”;再更细分,若个体是债券或 股票,则分别称为“债券组合”或“股票组合” 。 ⚫ 本节主要研究股票组合。 ⚫ 投资组合的目的是规避风险,不把所有的鸡蛋都放 在一个篮子里
13.1证券投资组合管理 13.1.2证券的收益与风险 一、单个证券的收益 1.如果已知某一证券全部收益结果出现的概率分布(见图 13-1),其预期收益率等于全部收益结果与发生概率之 积相加之总和: M E=∑R,P j=1 E为预期收益率;R,为证券i第j个收益率;R,为证券i第j个结果发生的概率。 图13-1某证券概率分布图
13.1.2 证券的收益与风险 13.1 证券投资组合管理 一、单个证券的收益 1. 如果已知某一证券全部收益结果出现的概率分布(见图 13-1),其预期收益率等于全部收益结果与发生概率之 积相加之总和: = = M j E R RijPij 1 ( ) E(R) 为预期收益率; Rij 为证券 i 第 j 个收益率; Rij 为证券 i 第 j 个结果发生的概率。 图13-1 某证券概率分布图 h r
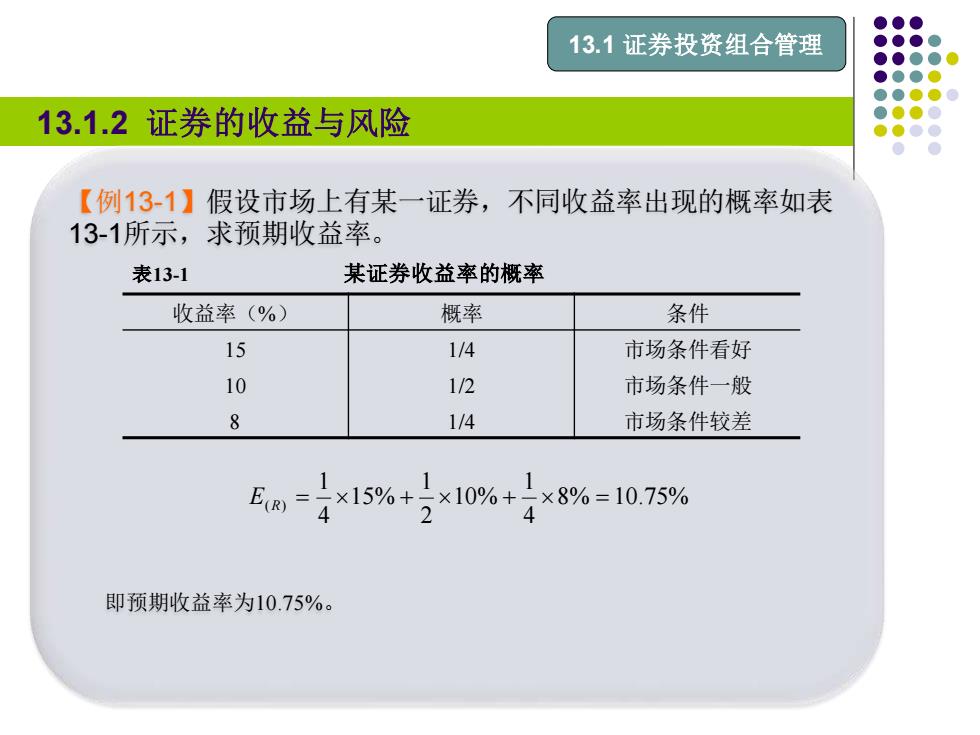
13.1证券投资组合管理 13.1.2证券的收益与风险 【例131】假设市场上有某一证券,不同收益率出现的概率如表 13-1所示,求预期收益率。 表13-1 某证券收益率的概率 收益率(%) 概率 条件 15 1/4 市场条件看好 10 1/2 市场条件一般 8 1/4 市场条件较差 E=4×15%+2×10%+4×8%=10.75% 即预期收益率为10.75%
13.1.2 证券的收益与风险 13.1 证券投资组合管理 【例13-1】假设市场上有某一证券,不同收益率出现的概率如表 13-1所示,求预期收益率。 即预期收益率为10.75%。 表13-1 某证券收益率的概率 收益率(%) 概率 条件 15 1/4 市场条件看好 10 1/2 市场条件一般 8 1/4 市场条件较差 8% 10.75% 4 1 10% 2 1 15% 4 1 E(R) = + + =

13.1证券投资组合管理 13.1.2证券的收益与风险 2.如果每一个收益结果都是相等的,则可以用平均收益率R 来估计E,:例如假设未来各年的收益率分布都是一样 的,其时序为R,R2,RM,收益率的抽样平均值为: 【例13-2】上例证券收益结果假定是相等的,都是13,则预期收益 率为: EW=R=159%+10%+8% =11% 3
13.1.2 证券的收益与风险 13.1 证券投资组合管理 2. 如果每一个收益结果都是相等的,则可以用平均收益率 来估计 : 例如假设未来各年的收益率分布都是一样 的,其时序为 收益率的抽样平均值为: R E(R) R R R 1 2 M , ,, , = = M t Rt M R 1 1 【例13-2】上例证券收益结果假定是相等的,都是1/3,则预期收益 率为: 11% 3 15% 10% 8% ( ) = + + E R = R =

13.1证券投资组合管理 13.1.2证券的收益与风险 二、单个证券的风险 ●实际收益率围绕预期收益率波动,波动越大,投资风险就越大。 风险指标是测定投资优劣的第二个指标。测定证券风险的指标,通常是 用均方差和标准差。 。均方差:通常用抽样方差代替真实均方差来估计。 1 M M (R) (R-R)2 M O(R) P(Ry -R)2 j=1 i=l 【例133】上例中的均方差: 062-05-+00=1+8-1n2-867 或者 o2-5-102+500-12+58-12-867 该证券的标准差为 0W=VG®=8.67=294
13.1.2 证券的收益与风险 13.1 证券投资组合管理 二、单个证券的风险 ⚫ 实际收益率围绕预期收益率波动,波动越大,投资风险就越大。 ⚫ 风险指标是测定投资优劣的第二个指标。测定证券风险的指标,通常是 用均方差和标准差。 ⚫ 均方差:通常用抽样方差代替真实均方差来估计。 = = − M j i R Rij R M 1 2 2 ( ) ( ) 1 = = − M j R Pij Rij Rj 1 2 2 ( ) ( ) 【例13-3】上例中的均方差: 或者 该证券的标准差为 8.67 3 (15 11) (10 11) (8 11) 2 2 2 2 ( ) = − + − + − R = (8 11) 8.67 3 1 (10 11) 3 1 (15 11) 3 2 1 2 2 2 (R) = − + − + − = 8.67 2.94 2 (R) = (R) = =

13.1证券投资组合管理 13.1.2证券的收益与风险 三、证券组合的收益率 假定证券组合P是由种不同证券组成,其中每种证券所占的比例为 X1,X2,Xm, 证券组合的收益率是组合中各单个证券收益率的加权 平均。 E(p) ∑xR 非系统 四、证券组合的风险 系统性 性风险 风险 证券组合风险可归纳如下: (1)一种股票的风险由两部分组成,即可分散风险和不可分散风险: (2)可分散风险可通过证券组合来削减(图13-2); (3)不可分散风险由市场变动而产生,它对所有股票都有影响,不可通过 证券组合而消除。不可分散风险用B系数来衡量
13.1.2 证券的收益与风险 13.1 证券投资组合管理 三、证券组合的收益率 假定证券组合P是由m种不同证券组成,其中每种证券所占的比例为 证券组合的收益率是组合中各单个证券收益率的加权 平均。 四、证券组合的风险 证券组合风险可归纳如下: (1)一种股票的风险由两部分组成,即可分散风险和不可分散风险; (2)可分散风险可通过证券组合来削减(图13-2); (3)不可分散风险由市场变动而产生,它对所有股票都有影响,不可通过 证券组合而消除。不可分散风险用 系数来衡量。 x x x 1 2 , ,, m, = = N i P iRij E x 1 ( ) 非系统 性风险 系统性 风险