
计量经济学 第五章 异方差性
1 第五章 异方差性 计量经济学

与引丁:叉为接近具买的结论文竹 么? 根据四川省2000年21个地市州医疗机构数与人口数 资料,分析医疗机构与人口数量的关系,建立卫生 医疗机构数与人口数的回归模型。对模型估计的结 果如下: y=-563.0548+5.3735X (291.5778)(0.644284) 1=(1.931062)(8.340265) R2=0.7854562=0.774146F=69.56003 式中y表示卫生医疗机构数(个),X表示人口 数量(万人)。 2
2 引子:更为接近真实的结论是什 么? 根据四川省2000年21个地市州医疗机构数与人口数 资料,分析医疗机构与人口数量的关系,建立卫生 医疗机构数与人口数的回归模型。对模型估计的结 果如下: 式中 表示卫生医疗机构数(个), 表示人口 数量(万人)。 (291.5778) (0.644284) ˆ -563.0548 5.3735 Y X i i = + 2 R = 0.785456 2 R = 0.774146 F = 69.56003 t = (-1.931062) (8.340265) Y X

模型显示的结果和问题 人口数量对应参数的标准误差较小; ·t统计量远大于临界值,可决系数和修正的可决系数结果较 好,「检验结果明显显著; ●表明该模型的估计效果不错,可以认为人口数量每增加1万 人,平均说来医疗机构将增加5.3735人。 然而,这里得出的结论可能是不可靠的,平均说来每增加1 万人口可能并不需要增加这样多的医疗机构,所得结论并不 符合真实情况。 有什么充分的理由说明这一回归结果不可靠呢?更为接近 真实的结论又是什么呢?
3 模型显示的结果和问题 ● 人口数量对应参数的标准误差较小; ● t统计量远大于临界值,可决系数和修正的可决系数结果较 好,F检验结果明显显著; ● 表明该模型的估计效果不错,可以认为人口数量每增加1万 人,平均说来医疗机构将增加5.3735人。 然而,这里得出的结论可能是不可靠的,平均说来每增加1 万人口可能并不需要增加这样多的医疗机构,所得结论并不 符合真实情况。 有什么充分的理由说明这一回归结果不可靠呢?更为接近 真实的结论又是什么呢?

第五章异方差性 本章讨论四个问题: 。异方差的实质和产生的原因 。异方差产生的后果 。异方差的检测方法 ·异方差的补救
4 本章讨论四个问题: ●异方差的实质和产生的原因 ●异方差产生的后果 ●异方差的检测方法 ●异方差的补救 第五章 异 方 差 性

第一节异方差性的概念 本节基本内容: ●异方差性的实质 ●异方差产生的原因
5 第一节 异方差性的概念 本节基本内容: ●异方差性的实质 ●异方差产生的原因

一、异方差性的实质 同方差的含义 同方差性:对所有的i=1,2,n有: Var(u )=o2 (5.1) 因为方差是度量被解释变量Y的观测值围绕回归线 E)=阝+阝2X2,+阝3X+.+fa (5.2) 的分散程度,因此同方差性指的是所有观测值的 分散程度相同。 6
6 一 、异方差性的实质 同方差的含义 同方差性:对所有的 有: (5.1) 因为方差是度量被解释变量 的观测值围绕回归线 (5.2) 的分散程度,因此同方差性指的是所有观测值的 分散程度相同。 E 1 2 2 3 3 ( ) . i i i k ki Y == b +b X +b b X X + + i (i n =1,2,., ) 2 Var(ui ) = σ Y

异方差性的含义 设模型为 Y=阝+f2X2,+阝X3+.+阝X+4 i=12,.,n 如果对于模型中随机误差项u;有: Var(u)=6,i=1,2,3,n (5.3) 则称具有异方差性。进一步,把异方差看成是由于某 个解释变量的变化而引起的,则 Var(u)=o2=o'f(X) (5.4) >
7 设模型为 如果对于模型中随机误差项 有: 则称具有异方差性。进一步,把异方差看成是由于某 个解释变量的变化而引起的,则 异方差性的含义 ui 1 2 2 3 3 . 1,2,., Yi X i X i kXki i = b +b +b b + + + = u i n 2 Var( ) , 1, 2,3,., i i u = = s i n 2 2 Var( ) ( ) i i i u = = s s f X (5.4) (5.3)
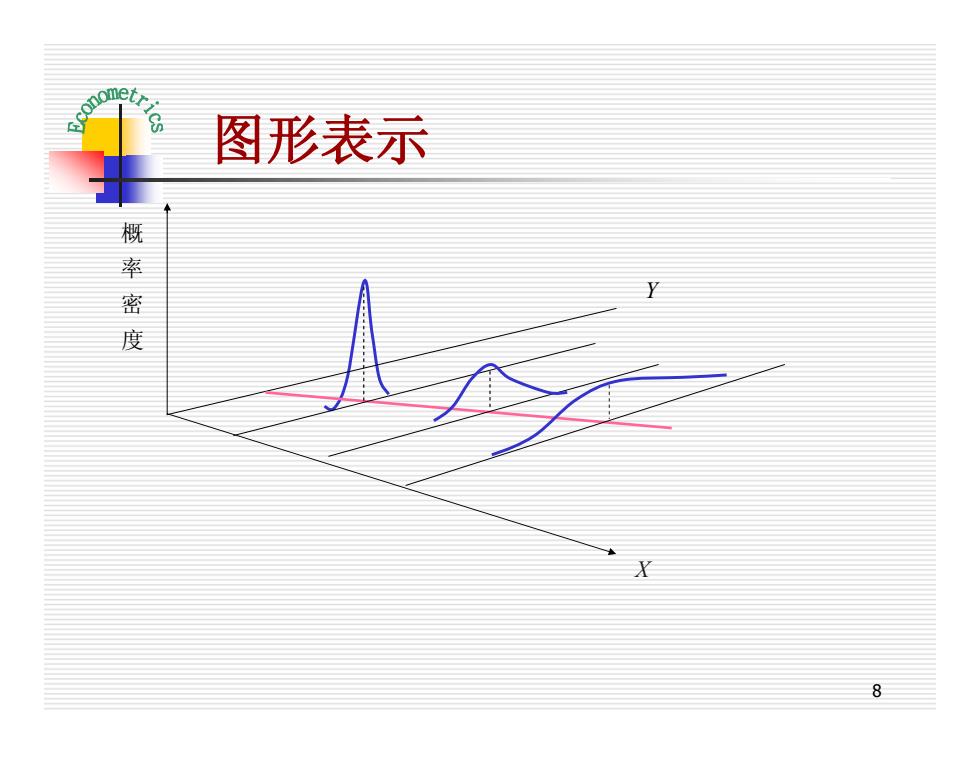
图形表示 概 密 度 8
8 图形表示 X Y 概 率 密 度

二、产生异方差的原因 (一)模型中省略了某些重要的解释变量 假设正确的计量模型是: Y=阝1+阝2X2+B3X3+4 假如略去X,而采用 Y,=B1+阝2X2+4 (5.5) 当被略去的X与X,有呈同方向或反方向变 化的趋势时,随X的有规律变化会体现在(5.5) 式的u中
9 (一)模型中省略了某些重要的解释变量 假设正确的计量模型是: 假如略去 ,而采用 当被略去的 与 有呈同方向或反方向变 化的趋势时,随 的有规律变化会体现在(5.5) 式的 中。 X3i Yi = b1 + b b 2X2i + + 3 3 X u i i X3i * Yi = b b 1 + + 2 2 X u i i X 3i X2i * i (u5.5) * i u X2i 二、产生异方差的原因

(二)模型的设定误差 模型的设定主要包括变量的选择和模型数学形式的确定。 模型中略去了重要解释变量常常导致异方差,实际就是模 型设定问题。除此而外,模型的函数形式不正确,如把变 量间本来为非线性的关系设定为线性,也可能导致异方 差。 (三)数据的测量误差 样本数据的观测误差有可能随研究范围的扩大而增加,或随 时间的推移逐步积累,也可能随着观测技术的提高而逐步 减小。 10
10 (二)模型的设定误差 模型的设定主要包括变量的选择和模型数学形式的确定。 模型中略去了重要解释变量常常导致异方差,实际就是模 型设定问题。除此而外,模型的函数形式不正确,如把变 量间本来为非线性的关系设定为线性,也可能导致异方 差。 (三)数据的测量误差 样本数据的观测误差有可能随研究范围的扩大而增加,或随 时间的推移逐步积累,也可能随着观测技术的提高而逐步 减小。 * i u