
第十章过关检测 (时间:60分钟满分:100分) 一、选择题(共10小题,每小题4分,共40分。在每小题给出的四个选项中,第 1~7小题只有一个选项符合题目要求,第8~10小题有多个选项符合题目要求,全 部选对的得4分,选对但不全的得2分,有选错或不答的得0分) 1关于电场强度和电势,下列说法正确的是() A.电场强度为零的地方,电势一定为零 B.在静电场中,沿电场方向电势逐渐降低 C.电荷一定会沿电场线方向移动 D.将一正的试探电荷从电势较低的等势面移到电势较高的等势面,电场力做正功 答案B 解桐电场强度为零的地方,电势不一定为零,例如等量同种电荷连线的中点处,选项A错误;在 静电场中,沿电场方向电势逐渐降低,选项B正确;电荷在电场中不一定会沿电场线方向移动, 与电荷的初速度方向、电场线的形状等都有关系,选项C错误;将一正的试探电荷从电势较 低的等势面移到电势较高的等势面,电势能增加,则电场力做负功,选项D错误。 2.下图为某示波管内的聚焦电场,实线和虚线分别表示电场线和等势线。两电子分别从α、b 两点运动到c点,设电场力对两电子做的功分别为W。和W,a、b点的电场强度大小分别为 Ea和Eb,则() A.Wa=Wb.Ea>Eb B.Wa≠Wb,Ea>Eb C.Wa=Wb.EaEb。选项A正确。 3.如图所示的匀强电场的电场强度为1.0×103N/C.ab平行于电场线.1ab=lcd=4cm.lac=lbd=3 cm。则下列计算结果正确的是( A.a、b之间的电势差为40V B.a、c之间的电势差为50V C.将gq=-5×103C的点电荷沿矩形路径abdca移动一周,静电力做的功是-0.25J D.将q=-5×103C的点电荷沿abd从a移到d,静电力做的功是0.25J 答案A
第十章过关检测 (时间:60 分钟 满分:100 分) 一、选择题(共 10 小题,每小题 4 分,共 40 分。在每小题给出的四个选项中,第 1~7 小题只有一个选项符合题目要求,第 8~10 小题有多个选项符合题目要求,全 部选对的得 4 分,选对但不全的得 2 分,有选错或不答的得 0 分) 1.关于电场强度和电势,下列说法正确的是( ) A.电场强度为零的地方,电势一定为零 B.在静电场中,沿电场方向电势逐渐降低 C.电荷一定会沿电场线方向移动 D.将一正的试探电荷从电势较低的等势面移到电势较高的等势面,电场力做正功 答案 B 解析电场强度为零的地方,电势不一定为零,例如等量同种电荷连线的中点处,选项 A 错误;在 静电场中,沿电场方向电势逐渐降低,选项 B 正确;电荷在电场中不一定会沿电场线方向移动, 与电荷的初速度方向、电场线的形状等都有关系,选项 C 错误;将一正的试探电荷从电势较 低的等势面移到电势较高的等势面,电势能增加,则电场力做负功,选项 D 错误。 2.下图为某示波管内的聚焦电场,实线和虚线分别表示电场线和等势线。两电子分别从 a、b 两点运动到 c 点,设电场力对两电子做的功分别为 Wa 和 Wb,a、b 点的电场强度大小分别为 Ea 和 Eb,则( ) A.Wa=Wb,Ea>Eb B.Wa≠Wb,Ea>Eb C.Wa=Wb,EaEb。选项 A 正确。 3.如图所示的匀强电场的电场强度为 1.0×103 N/C,ab 平行于电场线,lab=lcd=4 cm,lac=lbd=3 cm。则下列计算结果正确的是( ) A.a、b 之间的电势差为 40 V B.a、c 之间的电势差为 50 V C.将 q=-5×10-3 C 的点电荷沿矩形路径 abdca 移动一周,静电力做的功是-0.25 J D.将 q=-5×10-3 C 的点电荷沿 abd 从 a 移到 d,静电力做的功是 0.25 J 答案 A
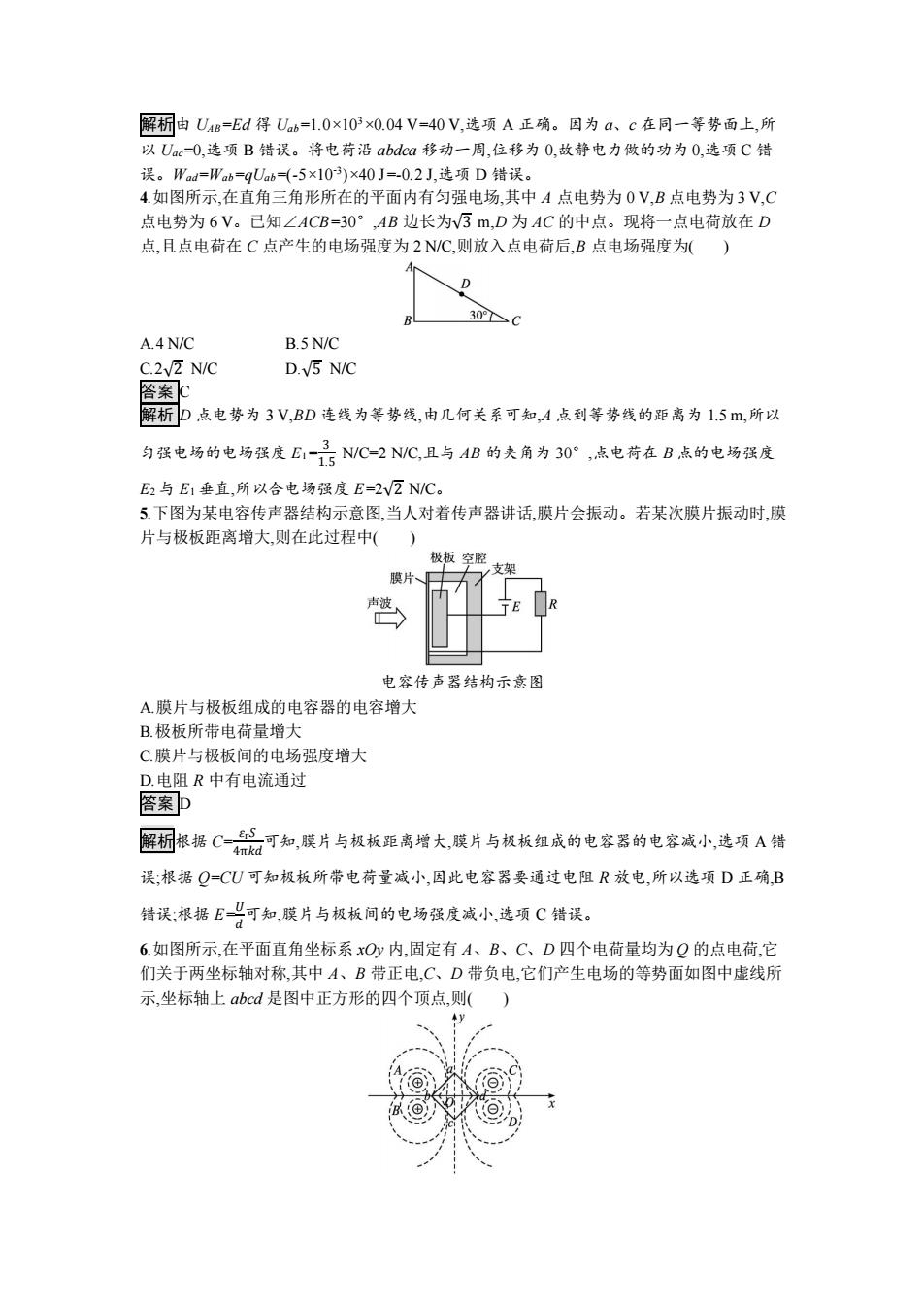
解标由U4B=Ed得Ua6=1.0×103×0.04V=40V,选项A正确。国为a、c在同一等势面上,所 以UacO,选项B错误。将电荷沿abdea移动一周,位移为0,故静电力做的功为0,选项C错 误。Wad=Wb=gUb=(-5×103)×40J=-0.2J,选项D错误。 4.如图所示,在直角三角形所在的平面内有匀强电场,其中A点电势为0V,B点电势为3V,C 点电势为6V。己知∠ACB=30°,AB边长为v3m,D为AC的中点。现将一点电荷放在D 点,且点电荷在C点产生的电场强度为2N/C,则放入点电荷后,B点电场强度为() 30C A.4N/C B.5 N/C C.2/2 N/C D.V5 N/C 答案 解析D点电势为3V,BD连线为等势线,由几何关系可知,A点到等势线的距离为1.5m,所以 匀强电场的电场强度E1品NWC-2NWC,且与AB的夫角为30°,点电荷在B点的电场强度 E2与E1垂直,所以合电场强度E=2VZN/C。 5.下图为某电容传声器结构示意图,当人对着传声器讲话,膜片会振动。若某次膜片振动时,膜 片与极板距离增大,则在此过程中( 极板空腔 支架 膜片、 声波 电容传声器结构示意图 A膜片与极板组成的电容器的电容增大 B.极板所带电荷量增大 C.膜片与极板间的电场强度增大 D.电阻R中有电流通过 答案D 解团根据C一品可知,膜片与极板距离增大,膜片与权板组成的电容器的电容减小,选项A错 误;根据Q=CU可知极板所带电荷量减小,因此电容器要通过电阻R放电,所以选项D正确,B 错误根据E-智可知,膜片与极板间的电场强度减小,选项C错误。 6.如图所示,在平面直角坐标系xOy内,固定有A、B、C、D四个电荷量均为Q的点电荷,它 们关于两坐标轴对称,其中A、B带正电,C、D带负电,它们产生电场的等势面如图中虚线所 示,坐标轴上abcd是图中正方形的四个顶点,则()
解析由 UAB=Ed 得 Uab=1.0×103×0.04 V=40 V,选项 A 正确。因为 a、c 在同一等势面上,所 以 Uac=0,选项 B 错误。将电荷沿 abdca 移动一周,位移为 0,故静电力做的功为 0,选项 C 错 误。Wad=Wab=qUab=(-5×10-3 )×40 J=-0.2 J,选项 D 错误。 4.如图所示,在直角三角形所在的平面内有匀强电场,其中 A 点电势为 0 V,B 点电势为 3 V,C 点电势为 6 V。已知∠ACB=30°,AB 边长为√3 m,D 为 AC 的中点。现将一点电荷放在 D 点,且点电荷在 C 点产生的电场强度为 2 N/C,则放入点电荷后,B 点电场强度为( ) A.4 N/C B.5 N/C C.2√2 N/C D.√5 N/C 答案 C 解析 D 点电势为 3 V,BD 连线为等势线,由几何关系可知,A 点到等势线的距离为 1.5 m,所以 匀强电场的电场强度 E1= 3 1.5 N/C=2 N/C,且与 AB 的夹角为 30°,点电荷在 B 点的电场强度 E2 与 E1 垂直,所以合电场强度 E=2√2 N/C。 5.下图为某电容传声器结构示意图,当人对着传声器讲话,膜片会振动。若某次膜片振动时,膜 片与极板距离增大,则在此过程中( ) 电容传声器结构示意图 A.膜片与极板组成的电容器的电容增大 B.极板所带电荷量增大 C.膜片与极板间的电场强度增大 D.电阻 R 中有电流通过 答案 D 解析根据 C= 𝜀r𝑆 4π𝑘𝑑可知,膜片与极板距离增大,膜片与极板组成的电容器的电容减小,选项 A 错 误;根据 Q=CU 可知极板所带电荷量减小,因此电容器要通过电阻 R 放电,所以选项 D 正确,B 错误;根据 E=𝑈 𝑑可知,膜片与极板间的电场强度减小,选项 C 错误。 6.如图所示,在平面直角坐标系 xOy 内,固定有 A、B、C、D 四个电荷量均为 Q 的点电荷,它 们关于两坐标轴对称,其中 A、B 带正电,C、D 带负电,它们产生电场的等势面如图中虚线所 示,坐标轴上 abcd 是图中正方形的四个顶点,则( )

A.b、d两点电势相等,电场强度不相等 B.b、d两点电场强度相同,电势不相等 C.将电子沿路径α→O→c移动,电场力做正功 D.将电子沿路径Q→b→c移动,电场力先做负功,后做正功 答案B 解桐根据对称性可知,b、d两点的电场强度大小相等,方向相同,均由b指向d,则电场强度相 同。b、d两点间的电场线由b指向d,所以b点的电势高于d点的电势,故选项A错误,B正 确;将电子沿路径α→O→c移动,电势不变,静电力不做功,故选项C错误;将电子沿路径 a→b→c移动,从a到b,电场力做正功,从b到c,电场力做负功,故选项D错误。 7两个点电荷Q1、Q2位于x轴上A、B两点,若取无限远处的电势为零,则在它们形成的电场 中,沿x轴正方向上各点的电势如图所示,且AP>PB。由图像提供的信息可知() AP点的电场强度为零 B.Q1的电荷量较大 C.电子沿x轴从A移到B的过程中,加速度逐渐减小 D.电子沿x轴从A移到B的过程中,电场力先做正功,后做负功 答案B 解韧该题中,-x图像的斜率大小表示该点的电场强度大小,E器由于P点的斜率不为零,所 以P点的电场强度不为零,选项A错误:从A到B电场强度先减小后增大,没有电场强度为零 的位置,所以两电荷为异种电荷,电场强度最小值的位置靠近Q2,所以Q1的电荷量较大,选项 B正确:加速度a所以电子沿x轴从A到B加速度先减小后增大,选项C错误:电场强度 71 的方向是从A指向B,所以电子沿x轴从A移到B的过程中,电场力一直做负功,选项D错 误。 8.如图所示,一带负电荷的油滴在匀强电场中运动,其轨迹在竖直面(纸面)内,且相对于过轨迹 最低点P的竖直线对称,忽略空气阻力。由此可知() 0 A.O点的电势比P点高 B.油滴在Q点的动能比它在P点的大 C.油滴在O点的电势能比它在P点的大 D.油滴在Q点的加速度大小比它在P点的小 答案AB 解析带电油滴在电场中受重力、电场力作用,据其轨迹的对称性可知,电场力方向竖直向上, 且电场力大于重力,电场力先做负功后做正功。则电场强度方向向下,Q点的电势比P,点高, 选项A正确。油滴在P点的速度最小,选项B正确。油滴在P点的电势能最大,选项C错 误。油滴运动的加速度大小不变,选项D错误
A.b、d 两点电势相等,电场强度不相等 B.b、d 两点电场强度相同,电势不相等 C.将电子沿路径 a→O→c 移动,电场力做正功 D.将电子沿路径 a→b→c 移动,电场力先做负功,后做正功 答案 B 解析根据对称性可知,b、d 两点的电场强度大小相等,方向相同,均由 b 指向 d,则电场强度相 同。b、d 两点间的电场线由 b 指向 d,所以 b 点的电势高于 d 点的电势,故选项 A 错误,B 正 确;将电子沿路径 a→O→c 移动,电势不变,静电力不做功,故选项 C 错误;将电子沿路径 a→b→c 移动,从 a 到 b,电场力做正功,从 b 到 c,电场力做负功,故选项 D 错误。 7.两个点电荷 Q1、Q2 位于 x 轴上 A、B 两点,若取无限远处的电势为零,则在它们形成的电场 中,沿 x 轴正方向上各点的电势如图所示,且 AP>PB。由图像提供的信息可知( ) A.P 点的电场强度为零 B.Q1 的电荷量较大 C.电子沿 x 轴从 A 移到 B 的过程中,加速度逐渐减小 D.电子沿 x 轴从 A 移到 B 的过程中,电场力先做正功,后做负功 答案 B 解析该题中,φ-x 图像的斜率大小表示该点的电场强度大小,E=Δ𝜑 Δ𝑥 ,由于 P 点的斜率不为零,所 以 P 点的电场强度不为零,选项 A 错误;从 A 到 B 电场强度先减小后增大,没有电场强度为零 的位置,所以两电荷为异种电荷,电场强度最小值的位置靠近 Q2,所以 Q1 的电荷量较大,选项 B 正确;加速度 a= 𝐸𝑞 𝑚 ,所以电子沿 x 轴从 A 到 B 加速度先减小后增大,选项 C 错误;电场强度 的方向是从 A 指向 B,所以电子沿 x 轴从 A 移到 B 的过程中,电场力一直做负功,选项 D 错 误。 8.如图所示,一带负电荷的油滴在匀强电场中运动,其轨迹在竖直面(纸面)内,且相对于过轨迹 最低点 P 的竖直线对称,忽略空气阻力。由此可知( ) A.Q 点的电势比 P 点高 B.油滴在 Q 点的动能比它在 P 点的大 C.油滴在 Q 点的电势能比它在 P 点的大 D.油滴在 Q 点的加速度大小比它在 P 点的小 答案 AB 解析带电油滴在电场中受重力、电场力作用,据其轨迹的对称性可知,电场力方向竖直向上, 且电场力大于重力,电场力先做负功后做正功。则电场强度方向向下,Q 点的电势比 P 点高, 选项 A 正确。油滴在 P 点的速度最小,选项 B 正确。油滴在 P 点的电势能最大,选项 C 错 误。油滴运动的加速度大小不变,选项 D 错误

mg 9.如图所示,水平面MN的下方存在竖直向下的匀强电场,一质量为m的带电小球由MN上方 的A点以一定初速度水平抛出,从B点进入电场,到达C点时速度方向恰好水平,A、B、C三 点在同一直线上,且IB=2lgc,由此可知 () A A.电场力为3mg B.小球带负电 C.小球从A到B与从B到C的运动时间相等 D.小球从A到B与从B到C的速度变化量相同 答案ABD 解桐由题意可得,从竖直方向看,小球初速度为0,先加速后减速到0从水平方向上看,小球做 匀速直线运动。因为14B=2lBC,故在做平抛运动时的水平位移是小球在电场中水平位移的2 倍,而水平方向的速度相等,所以平抛运动的时间是电场中运动时间的2倍。根据公式 2-2心,平抛运动的末速度和电场中运动的初速度相等,平抛运动的竖直位移是电场中竖直方 向位移的2倍,故电场中的加速度是平抛时加速度的2倍,因为平抛时的加速度为g,所以电场 运动时的加速度为2g,方向竖直向上,所以F电-mg=2mg,得电场力F电=3mg,选项A正确。小 球在竖直向下的电场中受向上的电场力,故小球带负电,选项B正确。小球从A到B与从B 到C的运动时间不相等,平抛运动的时间是电场中运动时间的2倍,选项C错误。因为 △v=al,A到B的速度变化量为g21,B到C的速度变化量为2g1,故它们是相等的,选项D正 确。 10.图中虚线α、b、cd、f代表匀强电场内间距相等的一组等势面,已知平面b上的电势为 2V。一电子经过a时的动能为l0eV,从a到d的过程中克服电场力所做的功为6eV。下 列说法正确的是() b A.平面c上的电势为零 B.该电子可能到达不了平面f C.该电子经过平面d时,其电势能为4eV D.该电子经过平面b时的速率是经过d时的2倍 答案AB 解析电子从a到d克服电场力做功6eV,则a、d之间的电势差为6V,匀强电场中间距相等 的等势面为等差等势面,所以平面a、b、c、d、f的电势依次为4V、2V、0V、-2V、-4V, 选项A正确:因为电子的运动方向不一定与等势面垂直,所以电子可能不会到达平面选项B 正确;电子从c到d,克服电场力做功2eV,电势能增加2eV,所以电子经过平面d时的电势能 为2eV,选项C错误;电子从a到b,克服电场力做功2eV,根据动能定理有10eV-2mv。2-2
9.如图所示,水平面 MN 的下方存在竖直向下的匀强电场,一质量为 m 的带电小球由 MN 上方 的 A 点以一定初速度水平抛出,从 B 点进入电场,到达 C 点时速度方向恰好水平,A、B、C 三 点在同一直线上,且 lAB=2lBC,由此可知 ( ) A.电场力为 3mg B.小球带负电 C.小球从 A 到 B 与从 B 到 C 的运动时间相等 D.小球从 A 到 B 与从 B 到 C 的速度变化量相同 答案 ABD 解析由题意可得,从竖直方向看,小球初速度为 0,先加速后减速到 0;从水平方向上看,小球做 匀速直线运动。因为 lAB=2lBC,故在做平抛运动时的水平位移是小球在电场中水平位移的 2 倍,而水平方向的速度相等,所以平抛运动的时间是电场中运动时间的 2 倍。根据公式 v 2=2ax,平抛运动的末速度和电场中运动的初速度相等,平抛运动的竖直位移是电场中竖直方 向位移的 2 倍,故电场中的加速度是平抛时加速度的 2 倍,因为平抛时的加速度为 g,所以电场 运动时的加速度为 2g,方向竖直向上,所以 F 电-mg=2mg,得电场力 F 电=3mg,选项 A 正确。小 球在竖直向下的电场中受向上的电场力,故小球带负电,选项 B 正确。小球从 A 到 B 与从 B 到 C 的运动时间不相等,平抛运动的时间是电场中运动时间的 2 倍,选项 C 错误。因为 Δv=at,A 到 B 的速度变化量为 g·2t,B 到 C 的速度变化量为 2g·t,故它们是相等的,选项 D 正 确。 10.图中虚线 a、b、c、d、f 代表匀强电场内间距相等的一组等势面,已知平面 b 上的电势为 2 V。一电子经过 a 时的动能为 10 eV,从 a 到 d 的过程中克服电场力所做的功为 6 eV。下 列说法正确的是( ) A.平面 c 上的电势为零 B.该电子可能到达不了平面 f C.该电子经过平面 d 时,其电势能为 4 eV D.该电子经过平面 b 时的速率是经过 d 时的 2 倍 答案 AB 解析电子从 a 到 d 克服电场力做功 6 eV, 则 a、d 之间的电势差为 6 V,匀强电场中间距相等 的等势面为等差等势面,所以平面 a、b、c、d、f 的电势依次为 4 V、2 V、0 V、-2 V、-4 V, 选项 A 正确;因为电子的运动方向不一定与等势面垂直,所以电子可能不会到达平面 f,选项 B 正确;电子从 c 到 d,克服电场力做功 2 eV,电势能增加 2 eV,所以电子经过平面 d 时的电势能 为 2 eV,选项 C 错误;电子从 a 到 b,克服电场力做功 2 eV,根据动能定理有 10 eV- 1 2 𝑚𝑣𝑏 2=2

eV,从a到d克服电场力做功6cV,根据动能定理有10eV号mva2-6cV,解得=V2,选项D 错误。 二、实验填空题(共2小题,共14分) 11.(4分)如图所示,有的计算机键盘的每一个键下面连一小块金属片,与该金属片隔有一定空 气间隙的是另一片小的固定金属片,这两片金属片组成一个小电容器。该电容器的电容C可 用公式C=计算,式中常量e=9×1012Fm,S表示金属片的正对面积,d表示两金属片间的距 离。当键被按下时,此小电容器的电容C发生变化,与之相连的电子线路就能检测出是哪个 键被按下了,从而给出相应的信号。设每个金属片的正对面积为50mm,键未按下时两金属 片间的距离为0.6mm。如果电容变化0.25pF,电子线路恰能检测出必要的信号,则键至少需 被按下 mm。 答案b.15 解桐初始位置的电容C- S_9x1012x50×10-6 F=7.5×1013F 0.6×103 d减小,C增大,电子线路恰能检测出必要的信号时的电容C-7.5×10-13F+2.5×1013F=1×1012 C=号则d-名0.45x103m=045mm,所以d的变化量为0.15mm,即钱至少需孩按下0.15 mm。 12.(10分)4、B、C是一条电场线上的三点,以B点为零电势点,一个电子从A移到B和C,电 场力做功分别为3.2×1019J和9.6×1019J,则电场线的方向为,A点的电势04 ,C点的电势pc=一。若C点为零电势点,则A点的电势p4= B 点的电势pB= 答案-→B→A-2V4V-6V-4V 解桐因为电子带负电,电场力做正功,所以电场力从A指向B,电场线方向正好相反,B指向A 所以电场线方向为C一B→A 做功WAB=UAB(-e) WAC=(UAB+UBC)(-e) UAB=-2V UBC=-4 V B点电势为零,所以pA=-2V 9c=4 V 如果以C点电势为零,A、B两,点电势均低于C点电势,则A点电势A=-6V,B点电势pB=-4 V。 三、计算题(共4小题,共46分。解答应写出必要的文字说明、方程式和重要演 算步骤,只写出最后答案的不能得分,有数值计算的题,答案中必须明确写出数值 和单位) 13.(10分)一水平放置的平行板电容器的两极板间距为d,极板分别与电池两极相连,上极板中 心有一小孔(小孔对电场的影响可忽略不计)。小孔正上方号处的P点有一带电粒子,该粒子从
eV,从 a 到 d,克服电场力做功 6 eV,根据动能定理有 10 eV- 1 2 𝑚𝑣𝑑 2=6 eV,解得𝑣𝑏 𝑣𝑑 = √2,选项 D 错误。 二、实验填空题(共 2 小题,共 14 分) 11.(4 分)如图所示,有的计算机键盘的每一个键下面连一小块金属片,与该金属片隔有一定空 气间隙的是另一片小的固定金属片,这两片金属片组成一个小电容器。该电容器的电容 C 可 用公式 C=ε 𝑆 𝑑计算,式中常量 ε=9×10-12 F/m,S 表示金属片的正对面积,d 表示两金属片间的距 离。当键被按下时,此小电容器的电容 C 发生变化,与之相连的电子线路就能检测出是哪个 键被按下了,从而给出相应的信号。设每个金属片的正对面积为 50 mm2 ,键未按下时两金属 片间的距离为 0.6 mm。如果电容变化 0.25 pF,电子线路恰能检测出必要的信号,则键至少需 被按下 mm。 答案 0.15 解析初始位置的电容 C=ε 𝑆 𝑑 = 9×10 -12×50×10 -6 0.6×10 -3 F=7.5×10-13 F d 减小,C 增大,电子线路恰能检测出必要的信号时的电容 C'=7.5×10-13 F+2.5×10-13 F=1×10-12 F C'=ε 𝑆 𝑑' ,则 d'=𝜀𝑆 𝐶' =0.45×10-3 m=0.45 mm,所以 d 的变化量为 0.15 mm,即键至少需被按下 0.15 mm。 12.(10 分)A、B、C 是一条电场线上的三点,以 B 点为零电势点,一个电子从 A 移到 B 和 C,电 场力做功分别为 3.2×10-19 J 和 9.6×10-19 J,则电场线的方向为 ,A 点的电势 φA = ,C 点的电势 φC= 。若 C 点为零电势点,则 A 点的电势 φA= ,B 点的电势 φB= 。 答案 C→B→A -2 V 4 V -6 V -4 V 解析因为电子带负电,电场力做正功,所以电场力从 A 指向 B,电场线方向正好相反,B 指向 A 所以电场线方向为 C→B→A 做功 WAB=UAB·(-e) WAC=(UAB+UBC)·(-e) UAB=-2 V UBC=-4 V B 点电势为零,所以 φA=-2 V φC=4 V 如果以 C 点电势为零,A、B 两点电势均低于 C 点电势,则 A 点电势 φA=-6 V,B 点电势 φB=-4 V。 三、计算题(共 4 小题,共 46 分。解答应写出必要的文字说明、方程式和重要演 算步骤,只写出最后答案的不能得分,有数值计算的题,答案中必须明确写出数值 和单位) 13.(10 分)一水平放置的平行板电容器的两极板间距为 d,极板分别与电池两极相连,上极板中 心有一小孔(小孔对电场的影响可忽略不计)。小孔正上方𝑑 2 处的 P 点有一带电粒子,该粒子从

静止开始下落,经过小孔进入电容器,并在下极板处(未与极板接触)返回。若将下极板向上平 移二求仍从P点由静止开始下落的相同粒子下落的最大高度。 靥案兴 解析粒子从小孔正上方号处由静止开始下落到下极板处返回,由动能定理有mg(号+d) 始d=0,与电池两极相连,电容器极板间电压不变,将下极板向上平移号后,设粒子下落距上极板 x处返回,由动能定理有mg侵+)日0,联立两式得x是下落的最大高度Hx号=头。 14.(10分)如图所示,在O点处固定一个正电荷,在过0点的竖直平面内的A点,自由释放一个 带正电的小球,小球的质量为m、电荷量为q。小球下落的轨迹如图中虚线所示,它与以O为 圆心、R为半径的圆相交于B、C两点,O、C在同一水平线上,∠BOC-30°,A距离OC的竖 直距离为h。若小球通过B点时的速度为y,试求: ④A 0④30: (I)小球通过C点时的速度大小 (2)小球由A到C的过程中电场力做的功。 含案1)√D2+gR(2片m2+2mgR-mgh 解标1)由题分析知B、C两点电势相等,则小球由B到C电场力做功为零,由动能定理有 mgRsin30°之mvc2-2m 得vc=Vv2+gR。 (2)由A到C应用动能定理有 Wac+mgh-imvc2-0 得Wac-2mvc2-mgh-22+与mgR-mgh。 15.(12分)如图所示,竖直平行正对放置的带电金属板A、B,B板中心的小孔正好位于平面直 角坐标系xOy的O点y轴沿竖直方向;在x>0的区域内存在沿y轴正方向的匀强电场,电场 强度大小为E-号×103V/m;比荷为1.0×105Cg的带正电粒子P从A板中心O'处静止释放, 其运动轨迹恰好经过M(v3m,1m)点:粒子P的重力不计
静止开始下落,经过小孔进入电容器,并在下极板处(未与极板接触)返回。若将下极板向上平 移 𝑑 2 ,求仍从 P 点由静止开始下落的相同粒子下落的最大高度。 答案3𝑑 4 解析粒子从小孔正上方𝑑 2处由静止开始下落到下极板处返回,由动能定理有 mg( 𝑑 2 + 𝑑)- q 𝑈 𝑑 d=0,与电池两极相连,电容器极板间电压不变,将下极板向上平移𝑑 2后,设粒子下落距上极板 x 处返回,由动能定理有 mg( 𝑑 2 + 𝑥)-q 𝑈 𝑑 2 x=0,联立两式得 x= 𝑑 4 ,下落的最大高度 H=x+𝑑 2 = 3𝑑 4 。 14.(10 分)如图所示,在 O 点处固定一个正电荷,在过 O 点的竖直平面内的 A 点,自由释放一个 带正电的小球,小球的质量为 m、电荷量为 q。小球下落的轨迹如图中虚线所示,它与以 O 为 圆心、R 为半径的圆相交于 B、C 两点,O、C 在同一水平线上,∠BOC=30°,A 距离 OC 的竖 直距离为 h。若小球通过 B 点时的速度为 v,试求: (1)小球通过 C 点时的速度大小; (2)小球由 A 到 C 的过程中电场力做的功。 答案(1)√𝑣 2 + 𝑔𝑅 (2)1 2 mv2+ 1 2 mgR-mgh 解析(1)由题分析知 B、C 两点电势相等,则小球由 B 到 C 电场力做功为零,由动能定理有 mgRsin 30°= 1 2 𝑚𝑣𝐶 2 − 1 2 mv2 得 vC=√𝑣 2 + 𝑔𝑅。 (2)由 A 到 C 应用动能定理有 WAC+mgh=1 2 𝑚𝑣𝐶 2 -0 得 WAC= 1 2 𝑚𝑣𝐶 2 -mgh=1 2 mv2+ 1 2 mgR-mgh。 15.(12 分)如图所示,竖直平行正对放置的带电金属板 A、B,B 板中心的小孔正好位于平面直 角坐标系 xOy 的 O 点;y 轴沿竖直方向;在 x>0 的区域内存在沿 y 轴正方向的匀强电场,电场 强度大小为 E=4 3 ×103 V/m;比荷为 1.0×105 C/kg 的带正电粒子 P 从 A 板中心 O'处静止释放, 其运动轨迹恰好经过 M(√3 m,1 m)点;粒子 P 的重力不计

y/m x/m (1I)求金属板A、B之间的电势差UABa (2)若在粒子P经过O点的同时,在y轴右侧匀强电场中某点由静止释放另一带电微粒Q,使 P、Q恰能在运动中相碰;假设Q的质量是P的2倍,带电情况与P相同:Q的重力及P、Q之 间的相互作用力均忽略不计:求粒子Q所有释放点的集合。 管案1)1000V(2y言,其中x20 解标1)设粒子P的质量为m、电荷量为q,从0点进入匀强电场时的速度大小为心,由题意 可知,粒子P在y轴右侧匀强电场中做类平抛运动;设从O点运动到M(V3m,1m),点历时为 0,由类平抛运动可得x=oo,-to2,解得w=2×10ms 2m 在金属板A、B之间,由动能定理得gUAB2mv02 解得UAB=1000V。 (2)设P、Q在右侧电场中运动的加速度分别为a1、a2:Q粒子从坐标N(x,y)点释放后,经时间 【与粒子P相遇。由牛顿运动定律及类平抛运动的规律和几何关系可得: 对于P有Eq=ma 对于Q有Eq=2ma2 x=10l 201P与y+2r2 1 解得y式,其中x>0 即粒子Q释放点N(x,y)坐标满足的方程为 ,其中x>0。 16.(14分)如图所示,用长为21的绝缘轻杆连接两个质量均为m的带电小球A和B置于光滑 绝缘的水平面上,A球的电荷量为+2q,B球的电荷量为-3q,构成一个带电系统(它们均可视为 质点,不计轻杆的质量,也不考虑两者间相互作用的库仑力)。现让小球A处在有界匀强电场 区域MPON内。己知虚线MP位于细杆的中垂线上,虚线NQ与MP平行且间距足够长。匀 强电场的电场强度大小为E,方向水平向右。释放带电系统,让它从静止开始运动,忽略带电 系统运动过程中所产生的磁场影响。求: (1)带电系统运动的最大速度:
(1)求金属板 A、B 之间的电势差 UAB。 (2)若在粒子 P 经过 O 点的同时,在 y 轴右侧匀强电场中某点由静止释放另一带电微粒 Q,使 P、Q 恰能在运动中相碰;假设 Q 的质量是 P 的 2 倍,带电情况与 P 相同;Q 的重力及 P、Q 之 间的相互作用力均忽略不计;求粒子 Q 所有释放点的集合。 答案(1)1 000 V (2)y= 1 6 x 2 ,其中 x>0 解析(1)设粒子 P 的质量为 m、电荷量为 q,从 O 点进入匀强电场时的速度大小为 v0;由题意 可知,粒子 P 在 y 轴右侧匀强电场中做类平抛运动;设从 O 点运动到 M(√3 m,1 m)点历时为 t0,由类平抛运动可得 x=v0t0,y= 𝑞𝐸 2𝑚 𝑡0 2 ,解得 v0=√2×104 m/s 在金属板 A、B 之间,由动能定理得 qUAB= 1 2 𝑚𝑣0 2 解得 UAB=1 000 V。 (2)设 P、Q 在右侧电场中运动的加速度分别为 a1、a2;Q 粒子从坐标 N(x,y)点释放后,经时间 t 与粒子 P 相遇。由牛顿运动定律及类平抛运动的规律和几何关系可得: 对于 P 有 Eq=ma1 对于 Q 有 Eq=2ma2 x=v0t 1 2 a1t 2=y+1 2 a2t 2 解得 y= 1 6 x 2 ,其中 x>0 即粒子 Q 释放点 N(x,y)坐标满足的方程为 y= 1 6 x 2 ,其中 x>0。 16.(14 分)如图所示,用长为 2l 的绝缘轻杆连接两个质量均为 m 的带电小球 A 和 B 置于光滑 绝缘的水平面上,A 球的电荷量为+2q,B 球的电荷量为-3q,构成一个带电系统(它们均可视为 质点,不计轻杆的质量,也不考虑两者间相互作用的库仑力)。现让小球 A 处在有界匀强电场 区域 MPQN 内。已知虚线 MP 位于细杆的中垂线上,虚线 NQ 与 MP 平行且间距足够长。匀 强电场的电场强度大小为 E,方向水平向右。释放带电系统,让它从静止开始运动,忽略带电 系统运动过程中所产生的磁场影响。求: (1)带电系统运动的最大速度;

(2)带电系统运动过程中,B球电势能增加的最大值; (3)带电系统回到初始位置所用时间。 图图厘(Q6g1(36= 解析()从A、B在电场中受力方向可知,小球B刚进入电场带电系统具有最大速度,从释放 常电系统到小球B刚进入电场的过程中,根据动能定理有2gE12muma2-0,= 29L (2)当带电系统速度第一次为零时,B球克服电场力做功最多,B球增加的电势能最多,设B球 在电场中的最大位移为x,由动能定理有2gE(l+x-3qEx=0,得x=21,所以B球电势能增加的最 大值为Wmax=3qE×21=6qE1。 (3)设带电系统由静止释放到小球B刚进入电场的过程中,带电系统运动的时间为1,则有 I1t12,1-器,设小球B进入电场后至小球A刚运动到带电系统速度为零时(最右端)的过程 中,常电系统运动的时间为么,则有2122票。根据对称性可知,带电系统从出发点回 到出发点的过程中所用总时间为12+22,解得1=6预 gE
(2)带电系统运动过程中,B 球电势能增加的最大值; (3)带电系统回到初始位置所用时间。 答案(1)√ 2𝑞𝐸𝑙 𝑚 (2)6qEl (3)6√ 2𝑚𝑙 𝑞𝐸 解析(1) 从 A、B 在电场中受力方向可知,小球 B 刚进入电场带电系统具有最大速度,从释放 带电系统到小球 B 刚进入电场的过程中,根据动能定理有 2qEl=1 2 ×2m𝑣max 2 -0,vmax=√ 2𝑞𝐸𝑙 𝑚 。 (2)当带电系统速度第一次为零时,B 球克服电场力做功最多,B 球增加的电势能最多,设 B 球 在电场中的最大位移为 x,由动能定理有 2qE(l+x)-3qEx=0,得 x=2l,所以 B 球电势能增加的最 大值为 Wmax=3qE×2l=6qEl。 (3)设带电系统由静止释放到小球 B 刚进入电场的过程中,带电系统运动的时间为 t1,则有 l=1 2 a1𝑡1 2 ,a1= 𝑞𝐸 𝑚 ;设小球 B 进入电场后至小球 A 刚运动到带电系统速度为零时(最右端)的过程 中,带电系统运动的时间为 t2,则有 2l=1 2 a2𝑡2 2 ,a2= 𝑞𝐸 2𝑚 。根据对称性可知,带电系统从出发点回 到出发点的过程中所用总时间为 t=2t1+2t2,解得 t=6√ 2𝑚𝑙 𝑞𝐸