
志鸿优化系列丛书 志鸿优化网,永远提供更新的! 丛书主编任志湖。 http://www.zhyh.org 第二章过关检测 (时间:90分钟满分:100分) 一、选择题(共10小题,每小题4分,共40分。在每小题给出的四个选项中,第1~7小题 只有一个选项符合题目要求,第8~10小题有多个选项符合题目要求,全部选对的得4分, 选对但不全的得2分,有选错或不答的得0分) 1.我们研究的匀变速直线运动是指() A位移随时间均匀变化 B.速度随时间均匀变化 C路程随时间均匀变化 D.加速度随时间均匀变化 答案B 解析匀变速直线运动是指加速度不变的直线运动,其速度随时间均匀变化,由公式x=o1+可知位 移随时间不是均匀变化,路程随时间也不是均匀变化,选项B正确。 2.下图是某物体做直线运动的1图像,由图像可得到的正确结果是() 4/ms-) 3.0 567t A.1=1s时物体的加速度大小为2m/s2 B.物体3s内的平均速度大小为2.5m/s C.物体7s内的位移为12m D.物体第3s内的位移为6m 含案 解析1图像斜钱的斜率代表加选度,由图像可知,a=m=1.5mS,选项A错误;平均速度节= △t 3s内的位移是图像与时间轴所国的面积,大小为6m,故-2m/5,选项B错误;物体7s内的位移即图 像7s内的面积,由梯形公式可得,位移大小为12m,选项C正确:第3s内的位移是图像第3s内的面 积,即矩形面积,由公式可得物体第3s内位移为3m,选项D错误。 3.两个物体从同一地点同时出发,向同一方向做匀变速直线运动,若它们的初速度不同而加速度相同, 则在运动过程中() A.它们的速度之差保持不变 B.它们的速度之差与时间成正比 1
1 第二章过关检测 (时间:90 分钟 满分:100 分) 一、选择题(共 10 小题,每小题 4 分,共 40 分。在每小题给出的四个选项中,第 1~7 小题 只有一个选项符合题目要求,第 8~10 小题有多个选项符合题目要求,全部选对的得 4 分, 选对但不全的得 2 分,有选错或不答的得 0 分) 1.我们研究的匀变速直线运动是指( ) A.位移随时间均匀变化 B.速度随时间均匀变化 C.路程随时间均匀变化 D.加速度随时间均匀变化 答案:B 解析:匀变速直线运动是指加速度不变的直线运动,其速度随时间均匀变化,由公式 x=v0t+1 2 at2 可知位 移随时间不是均匀变化,路程随时间也不是均匀变化,选项 B 正确。 2.下图是某物体做直线运动的 v-t 图像,由图像可得到的正确结果是( ) A.t=1 s 时物体的加速度大小为 2 m/s2 B.物体 3 s 内的平均速度大小为 2.5 m/s C.物体 7 s 内的位移为 12 m D.物体第 3 s 内的位移为 6 m 答案:C 解析:v-t 图像斜线的斜率代表加速度,由图像可知,a= Δ𝑣 Δ𝑡 = 3 2 m/s2=1.5 m/s2 ,选项 A 错误;平均速度𝑣 = 𝑥 𝑡 ,3 s 内的位移是图像与时间轴所围的面积,大小为 6 m,故𝑣=2 m/s,选项 B 错误;物体 7 s 内的位移即图 像 7 s 内的面积,由梯形公式可得,位移大小为 12 m,选项 C 正确;第 3 s 内的位移是图像第 3 s 内的面 积,即矩形面积,由公式可得物体第 3 s 内位移为 3 m,选项 D 错误。 3.两个物体从同一地点同时出发,向同一方向做匀变速直线运动,若它们的初速度不同而加速度相同, 则在运动过程中( ) A.它们的速度之差保持不变 B.它们的速度之差与时间成正比

志鸿优化系列丛书 志鸿优化网,永远提供更新的! 丛书主编任志湖。 http://www.zhyh.org C.它们的位移之差与时间的二次方成正比 D.它们的位移之差与时间成反比 答案A 解析两物体从同一地点同时出发,沿同一方向做匀变速直线运动,初速度不同,加速度相同。根据匀 变速直线运动规律,有y1=o1+al,2=o2+al,得2-M=o2-01,选项A正确,B错误;又 x1=o11+与ar2,x2=o21+与a2,得x2-x1-(o2-o1)1,选项C、D错误。 4.如图所示,甲从A地由静止匀加速跑向B地,当甲前进距离为x1时,乙从距A地?处的C点由静止 出发,加速度与甲相同,最后二人同时到达B地,则AB两地距离为() 甲 A.x1+2 B1+x22 4x1 2 C-4x1+x2】 D.x1+x2)2 "(x1-x2)x1 含案B 解析设甲前进距离为1时,速度为,甲和乙做匀加速直线运动的加速度为a,则有m+a㎡之P=-, 根据速度位移公式得P2解得1震则AB的距离r2选项B正喻。 2ax1 4x1 5.高速公路的ETC电子收费系统如图所示,ETC通道的长度是识别区起点到自动栏杆的水平距离。 某汽车以21.6k/h的速度匀速进入识别区,ET℃天线用了0.3s的时间识别车载电子标签,识别完成 后发出“滴”的一声,司机发现自动栏杆没有抬起,于是采取制动刹车,汽车刚好没有撞杆。已知司机的 反应时间为0.7s,刹车的加速度大小为5m/s2,则该ETC通道的长度约为() 自动栏杆 ETC天线 电子标签 A.4.2m B.6.0m C.7.8m D.9.6m 含案p 2
2 C.它们的位移之差与时间的二次方成正比 D.它们的位移之差与时间成反比 答案:A 解析:两物体从同一地点同时出发,沿同一方向做匀变速直线运动,初速度不同,加速度相同。根据匀 变速直线运动规律,有 v1=v01+at,v2=v02+at,得 v2-v1=v02-v01,选项 A 正确,B 错误;又 x1=v01t+1 2 at2 ,x2=v02t+1 2 at2 ,得 x2-x1=(v02-v01)t,选项 C、D 错误。 4.如图所示,甲从 A 地由静止匀加速跑向 B 地,当甲前进距离为 x1 时,乙从距 A 地 x2处的 C 点由静止 出发,加速度与甲相同,最后二人同时到达 B 地,则 AB 两地距离为( ) A.x1+x2 B. (𝑥1+𝑥2) 2 4𝑥1 C. 𝑥1 2 4(𝑥1+𝑥2) D. (𝑥1+𝑥2) 2 (𝑥1-𝑥2)𝑥1 答案:B 解析:设甲前进距离为 x1 时,速度为 v,甲和乙做匀加速直线运动的加速度为 a,则有 vt+1 2 at2 - 1 2 at2=x2-x1, 根据速度位移公式得 v 2=2ax1,解得 t= 𝑥2-𝑥1 √2𝑎𝑥1 ,则 AB 的距离 x=x2+ 1 2 at2= (𝑥1+𝑥2) 2 4𝑥1 ,选项 B 正确。 5.高速公路的 ETC 电子收费系统如图所示,ETC 通道的长度是识别区起点到自动栏杆的水平距离。 某汽车以 21.6 km/h 的速度匀速进入识别区,ETC 天线用了 0.3 s 的时间识别车载电子标签,识别完成 后发出“滴”的一声,司机发现自动栏杆没有抬起,于是采取制动刹车,汽车刚好没有撞杆。已知司机的 反应时间为 0.7 s,刹车的加速度大小为 5 m/s2 ,则该 ETC 通道的长度约为( ) A.4.2 m B.6.0 m C.7.8 m D.9.6 m 答案:D

志鸿优化系列丛书 志鸿优化网,永远提供更新的! 丛书主编任志河。 http://www.zhyh.org 解析汽车的初速度0=21.6km/h=6m/s,汽车在前0.3s+0.7s内做匀速直线运动,位移为 =w+)=6×(0.3+0.7)-=6m,随后汽车做匀减速运动,位移为四= 62 2a=2x5m=3.6m,所以该ETC通 道的长度为1=x1+2=6m+3.6m-9.6m,故选项A、B、C错误,D正确。 6.一个从地面上竖直上抛的物体,它两次经过一个较低点A的时间间隔是5s,两次经过一个较高点B 的时间间隔是3s,则AB之间的距离是(g取10m/s2)() A.80m B.40m C.20m D.初速度未知.无法确定 答案 解析小球做竖直上抛运动,根据运动时间的对称性得到物体从最高点自由下落到A点的时间为头最 高点到B点的时间为号AB间距离为1s9(侵)-9(学)=x10x(2.15的m=-20m,选项C正 确。 7.甲、乙两物体在同一直线上运动的x1图像如图所示,以甲的出发点为原点,出发时刻为计时起点, 则以下说法不正确的是( ) x/m A.甲、乙同时出发 B.乙比甲先出发 C.甲开始运动时,乙在甲前面和处 D.甲在中途停了一会儿,但最后还是追上了乙 答案B 解析匀速直线运动的x1图像是一条倾斜的直线,直线与纵坐标的交点表示出发时物体离原点的距 离。当直线与1轴平行时,表示物体位置不变,处于静止,两直线的交点表示两物体处在同一位置,离原 点距离相等。选项A、C、D正确,B错误。 8.一列长I的火车以加速度α匀加速经过一座长为x的直桥(<x),火车通过桥头和桥尾的时间分别是 1和2,则() A火车通过桥头的平均速度是 1 B火车通过桥头的平均速度是 Γt1 3
3 解析:汽车的初速度 v0=21.6 km/h=6 m/s,汽车在前 0.3 s+0.7 s 内做匀速直线运动,位移为 x1=v0(t1+t2)=6×(0.3+0.7)=6 m,随后汽车做匀减速运动,位移为 x2= 𝑣0 2 2𝑎 = 6 2 2×5 m=3.6 m,所以该 ETC 通 道的长度为 l=x1+x2=6 m+3.6 m=9.6 m,故选项 A、B、C 错误,D 正确。 6.一个从地面上竖直上抛的物体,它两次经过一个较低点 A 的时间间隔是 5 s,两次经过一个较高点 B 的时间间隔是 3 s,则 AB 之间的距离是(g 取 10 m/s2 )( ) A.80 m B.40 m C.20 m D.初速度未知,无法确定 答案:C 解析:小球做竖直上抛运动,根据运动时间的对称性得到物体从最高点自由下落到 A 点的时间为𝑡𝐴 2 ,最 高点到 B 点的时间为𝑡𝐵 2 ,AB 间距离为 hAB= 1 2 𝑔 ( 𝑡𝐴 2 ) 2 − 1 2 𝑔 ( 𝑡𝐵 2 ) 2 = 1 2 ×10×(2.5 2 -1.5 2 ) m=20 m,选项 C 正 确。 7.甲、乙两物体在同一直线上运动的 x-t 图像如图所示,以甲的出发点为原点,出发时刻为计时起点, 则以下说法不正确的是( ) A.甲、乙同时出发 B.乙比甲先出发 C.甲开始运动时,乙在甲前面 x0 处 D.甲在中途停了一会儿,但最后还是追上了乙 答案:B 解析:匀速直线运动的 x-t 图像是一条倾斜的直线,直线与纵坐标的交点表示出发时物体离原点的距 离。当直线与 t 轴平行时,表示物体位置不变,处于静止,两直线的交点表示两物体处在同一位置,离原 点距离相等。选项 A、C、D 正确,B 错误。 8.一列长 l 的火车以加速度 a 匀加速经过一座长为 x 的直桥(l<x),火车通过桥头和桥尾的时间分别是 t1 和 t2,则( ) A.火车通过桥头的平均速度是 𝑙 𝑡1 B.火车通过桥头的平均速度是𝑥 𝑡1

志鸿优化系列丛书 志鸿优化网,永远提供更新的! 丛书主编任志湖。 http://www.zhyh.org C.火车头从桥头到桥尾的时间是) at t2 D.火车头从桥头到桥尾的时间是:2+ atit2 7 答案AD 解析火车通过桥头的时间为,根据平均速度公式可知,火车通过桥头的平均速度 m宁 故选项B错误,A正确: 火车通过桥尾的时间为2,根据平均速度公式可知,火车通过桥尾的平均速度 分 根据平均速度定义可知,火车头到桥头的速度 %m号 火车头到桥尾的速度 w=n-6号 则火车头从桥头到桥尾的时间 14=2+电 a att2 故选项C错误,D正确。 9.汽车A在红绿灯前停住,绿灯亮起时启动,以0.4m/s2的加速度做匀加速直线运动,30s后以该时刻 的速度做匀速直线运动:设在绿灯亮的同时,汽车B以8m/s的速度从A车旁边驶过,且一直以此速度 做匀速直线运动,运动方向与A车相同,则从绿灯亮时开始() A.A车在加速过程中与B车相遇 B.A、B两车相遇时速度相同 C,相遇时A车做匀速运动 D.A车追上B车后,两车不可能再次相遇 答案CD 解标A车在匀加速直线运动过程中的位移xA10At12=180m,此过程中B车的位移xB1=阳1-240 m>xA1,故A车在加速过程中没有与B车相遇,选项A错误,C正确;之后因vA=QAt1=12m/s>B,故A车 一定能追上B车,相遇之后不能再相遇,A、B相遇时的速度一定不相同,选项B错误,D正确。 10.物体甲的x-1图像和物体乙的-1图像分别如图所示,则这两个物体的运动情况是()
4 C.火车头从桥头到桥尾的时间是𝑙(𝑡1 -𝑡2 ) 𝑎𝑡1 𝑡2 D.火车头从桥头到桥尾的时间是𝑙(𝑡1 -𝑡2 ) 𝑎𝑡1 𝑡2 + 𝑡1 -𝑡2 2 答案:AD 解析:火车通过桥头的时间为 t1,根据平均速度公式可知,火车通过桥头的平均速度 v1= 𝑙 𝑡1 故选项 B 错误,A 正确; 火车通过桥尾的时间为 t2,根据平均速度公式可知,火车通过桥尾的平均速度 v2= 𝑙 𝑡2 根据平均速度定义可知,火车头到桥头的速度 v3=v1-a 𝑡1 2 火车头到桥尾的速度 v4=v2-a 𝑡2 2 则火车头从桥头到桥尾的时间 t= 𝑣4-𝑣3 𝑎 = 𝑙(𝑡1 -𝑡2 ) 𝑎𝑡1 𝑡2 + 𝑡1 -𝑡2 2 故选项 C 错误,D 正确。 9.汽车 A 在红绿灯前停住,绿灯亮起时启动,以 0.4 m/s2 的加速度做匀加速直线运动,30 s 后以该时刻 的速度做匀速直线运动;设在绿灯亮的同时,汽车 B 以 8 m/s 的速度从 A 车旁边驶过,且一直以此速度 做匀速直线运动,运动方向与 A 车相同,则从绿灯亮时开始( ) A.A 车在加速过程中与 B 车相遇 B.A、B 两车相遇时速度相同 C.相遇时 A 车做匀速运动 D.A 车追上 B 车后,两车不可能再次相遇 答案:CD 解析:A 车在匀加速直线运动过程中的位移 xA1= 1 2 aA𝑡1 2=180 m,此过程中 B 车的位移𝑥B1 =vBt1=240 m>xA1,故 A 车在加速过程中没有与 B 车相遇,选项 A 错误,C 正确;之后因 vA=aAt1=12 m/s>vB,故 A 车 一定能追上 B 车,相遇之后不能再相遇,A、B 相遇时的速度一定不相同,选项 B 错误,D 正确。 10.物体甲的 x-t 图像和物体乙的 v-t 图像分别如图所示,则这两个物体的运动情况是( )

志鸿优化系列丛书 志鸿优化网,永远提供更新的: 丛书主编任志湖。 http://www.zhyh.org x/m 4vm·s) 6 6 t/s 乙 A.甲在整个1=6s时间内运动方向一直不变,它通过的总位移大小为4m B.甲在整个1=6s时间内有往复运动,它通过的总位移为零 C.乙在整个1=6s时间内有往复运动,它通过的总位移为零 D.乙在整个1=6s时间内加速度方向一直不变,它通过的总路程为6m 答案ACD 解析甲的速度v,2:2m/s子m6,故甲一直向正方向运动,位移x=2m(-2m)=4m,选项A正确,B 6 错误。乙在0-3s内的位移1=-3m,36s内的位移2=3m,6s内乙的总位移x=x1+2=0,且乙先向负 向运动,又向正向运动,做往复运动,总路程为x+2=6m,乙图像的斜率不变,说明加速度方向不变,选 项C、D正确。 二、实验题(共2小题,共18分) 11.(8分)1)在利用自由落体运动测重力加速度的实验中用到如图甲、乙所示的两种打点计时器,请 回答下面的问题: 限位孔 振针 永久磁铁 线圈 复写纸 限位孔 振片 甲 墨粉纸盒 脉冲开心星 ⊙压纸条 纸盒轴 子纸带 电源插头 乙 图乙是」 (选填“电磁打点”或“电火花)计时器,电源采用的是 (选填“交流8 V*交流220或“四节干电池)。 (2)某同学用如图甲所示装置测量自由落体加速度g,得到如图丙所示的一段纸带,他每两个点取一个 计数点(已知交变电流频率为50Hz),测得AB-7.65cm,BC-9.17cm。则打B点时重物的瞬时速度为 m/s,测得的自由落体加速度g=m/s2,它比真实值偏 (选填“大”或“小”。(结果保留两 位有效数字) 5
5 A.甲在整个 t=6 s 时间内运动方向一直不变,它通过的总位移大小为 4 m B.甲在整个 t=6 s 时间内有往复运动,它通过的总位移为零 C.乙在整个 t=6 s 时间内有往复运动,它通过的总位移为零 D.乙在整个 t=6 s 时间内加速度方向一直不变,它通过的总路程为 6 m 答案:ACD 解析:甲的速度 v 甲= 2-(-2) 6 m/s= 2 3 m/s,故甲一直向正方向运动,位移 x 甲=2 m-(-2 m)=4 m,选项 A 正确,B 错误。乙在 0~3 s 内的位移 x1=-3 m,3~6 s 内的位移 x2=3 m,6 s 内乙的总位移 x=x1+x2=0,且乙先向负 向运动,又向正向运动,做往复运动,总路程为|x1|+x2=6 m,乙图像的斜率不变,说明加速度方向不变,选 项 C、D 正确。 二、实验题(共 2 小题,共 18 分) 11.(8 分)(1)在利用自由落体运动测重力加速度的实验中用到如图甲、乙所示的两种打点计时器,请 回答下面的问题: 甲 乙 图乙是 (选填“电磁打点”或“电火花”)计时器,电源采用的是 (选填“交流 8 V”“交流 220 V”或“四节干电池”)。 (2)某同学用如图甲所示装置测量自由落体加速度 g,得到如图丙所示的一段纸带,他每两个点取一个 计数点(已知交变电流频率为 50 Hz),测得 AB=7.65 cm,BC=9.17 cm。则打 B 点时重物的瞬时速度为 m/s,测得的自由落体加速度 g= m/s2 ,它比真实值偏 (选填“大”或“小”)。(结果保留两 位有效数字)
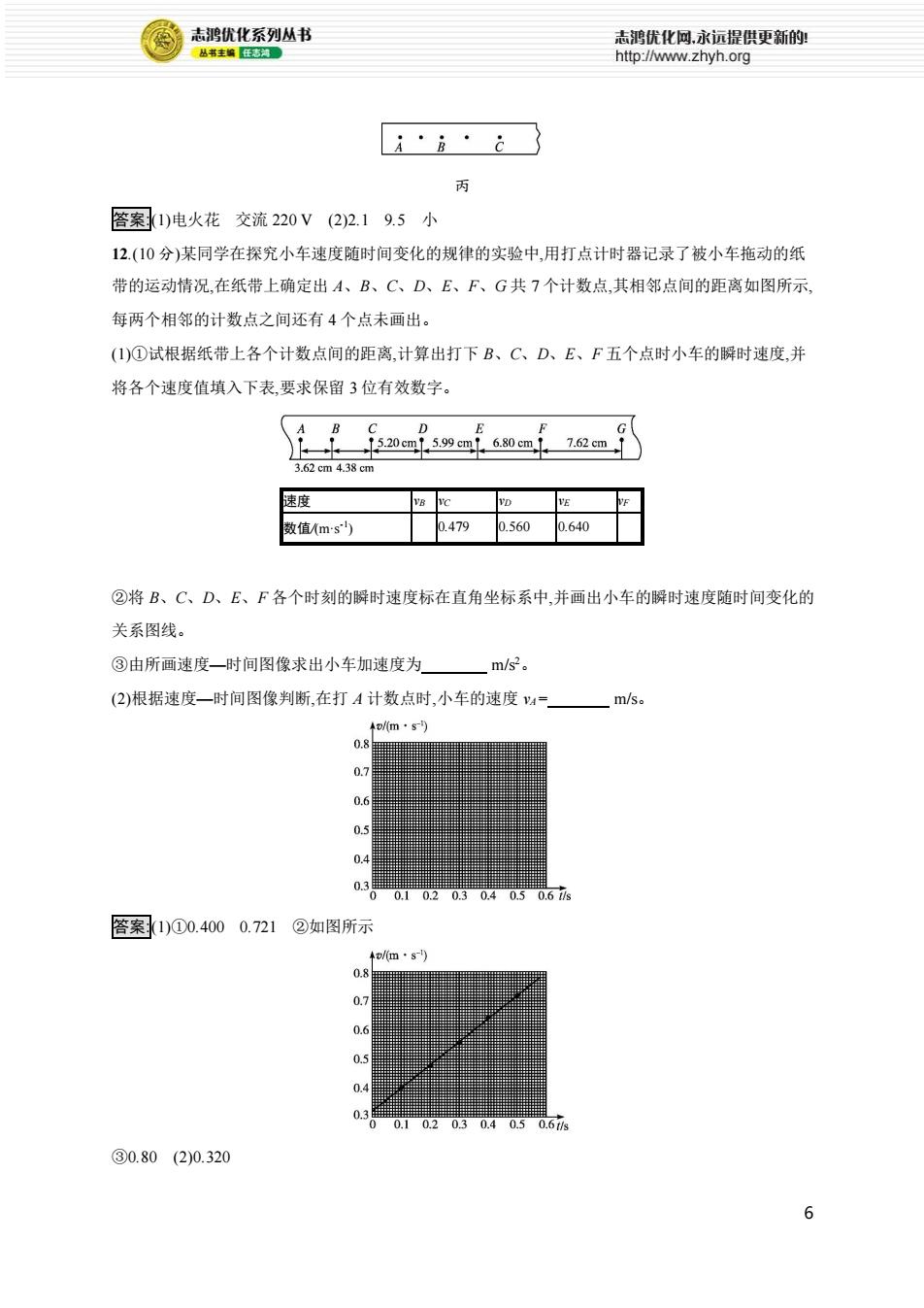
志鸿优化系列丛书 志鸿优化网,永远提供更新的: 丛书主编任志湖。 http://www.zhyh.org 的 案)电火花交流220V(22.19.5小 12.(10分)某同学在探究小车速度随时间变化的规律的实验中,用打点计时器记录了被小车拖动的纸 带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点,其相邻点间的距离如图所示, 每两个相邻的计数点之间还有4个点未画出。 (1)①试根据纸带上各个计数点间的距离,计算出打下B、C、D、E、F五个点时小车的瞬时速度,并 将各个速度值填入下表,要求保留3位有效数字。 D G 7.62cm 3.62cm4.38cm 速度 VD VE VF 数值《msl) 0.479 0.560 0.640 ②将B、C、D、E、F各个时刻的瞬时速度标在直角坐标系中,并画出小车的瞬时速度随时间变化的 关系图线。 ③由所画速度一时间图像求出小车加速度为 m/s2。 (2)根据速度一时间图像判断,在打A计数点时,小车的速度4=一ms。 4/m·s 0.8 0.t 0.5 0.4 0.3 00.10.20.30.40.50.6tis 客案1)①0.4000.721( ②如图所示 ↑m·s-) 0.8 0.7 0.6 0.4 0.3 00.10.20.30.40.50.6t/ ③0.80(2)0.320 6
6 丙 答案:(1)电火花 交流 220 V (2)2.1 9.5 小 12.(10 分)某同学在探究小车速度随时间变化的规律的实验中,用打点计时器记录了被小车拖动的纸 带的运动情况,在纸带上确定出 A、B、C、D、E、F、G 共 7 个计数点,其相邻点间的距离如图所示, 每两个相邻的计数点之间还有 4 个点未画出。 (1)①试根据纸带上各个计数点间的距离,计算出打下 B、C、D、E、F 五个点时小车的瞬时速度,并 将各个速度值填入下表,要求保留 3 位有效数字。 速度 vB vC vD vE vF 数值/(m·s -1 ) 0.479 0.560 0.640 ②将 B、C、D、E、F 各个时刻的瞬时速度标在直角坐标系中,并画出小车的瞬时速度随时间变化的 关系图线。 ③由所画速度—时间图像求出小车加速度为 m/s2。 (2)根据速度—时间图像判断,在打 A 计数点时,小车的速度 vA= m/s。 答案:(1)①0.400 0.721 ②如图所示 ③0.80 (2)0.320

志鸿优化系列丛书 志鸿优化网,永远提供更新的! 丛书主编任志湖。 http://www.zhyh.org 匠108点的瞬时速度为%兴-62010 m/s=0.400m/s 2×0.10 F点的瞬时速度为 g票=602x1 -m/s=0.721m/s。 2×0.10 ②将B、C、D、E、F各个时刻的瞬时速度标在直角坐标系中,并画出小车的瞬时速度随时间变化的 关系图线,见答案。 ③由所画速度一时间图像,在图线上取点(0,0.320.4,0.64),结合图线的斜率知,a064-032ms-0.80 0.4 m/s32。 (2)根据速度一时间图像判断,图线与纵轴的交点,即为A点的速度大小,那么在打A计数点时,小车的 速度为v4=0.320m/s。 三、计算题(共4小题,共42分。解答应写出必要的文字说明、方程式和重要演算步骤, 只写出最后答案不能得分,有数值计算的题,答案中必须明确写出数值和单位)》 13.(8分)一小球从空中某高处由静止释放,经3s落地,求小球下落的高度h和小球在下落过程中第2 s内的位移(不计空气阻力,g取10m/s2)。 答案45m15m 解析小球下落时的高度 h23r2之×10x32m=45m 小球第25内的位移可由公式阳23m求出 2g 由V1=g11,2=g12知 a202102 2×10m-15m。 14.(10分)一辆汽车从静止开始做匀加速直线运动,已知途中先后经过相距27m的A、B两点所用时 间为2s,汽车经过B点时的速度为15m/s。求: (I)汽车经过A点时的速度大小, (2)汽车从出发点到A点的位移及平均速度大小。 客案1)12ms (2)48m6m/s 解析设汽车运动方向为正方向,则 VB=15 m/s,t4B=2 S.XAB=27 m 7
7 解析:(1)①B 点的瞬时速度为 vB= 𝑥𝐴𝐶 2𝑇 = (3.62+4.38)×10 -2 2×0.10 m/s=0.400 m/s F 点的瞬时速度为 vF= 𝑥𝐸𝐺 2𝑇 = (6.80+7.62)×10 -2 2×0.10 m/s=0.721 m/s。 ②将 B、C、D、E、F 各个时刻的瞬时速度标在直角坐标系中,并画出小车的瞬时速度随时间变化的 关系图线,见答案。 ③由所画速度—时间图像,在图线上取点(0,0.32)(0.4,0.64),结合图线的斜率知,a= 0.64-0.32 0.4 m/s2=0.80 m/s2。 (2)根据速度—时间图像判断,图线与纵轴的交点,即为 A 点的速度大小,那么在打 A 计数点时,小车的 速度为 vA=0.320 m/s。 三、计算题(共 4 小题,共 42 分。解答应写出必要的文字说明、方程式和重要演算步骤, 只写出最后答案不能得分,有数值计算的题,答案中必须明确写出数值和单位) 13.(8 分)一小球从空中某高处由静止释放,经 3 s 落地,求小球下落的高度 h 和小球在下落过程中第 2 s 内的位移(不计空气阻力,g 取 10 m/s2 )。 答案:45 m 15 m 解析:小球下落时的高度 h=1 2 gt2= 1 2 ×10×3 2 m=45 m 小球第 2 s 内的位移可由公式 h2= 𝑣2 2 -𝑣1 2 2𝑔 求出 由 v1=gt1,v2=gt2 知 h2= 20 2 -10 2 2×10 m=15 m。 14.(10 分)一辆汽车从静止开始做匀加速直线运动,已知途中先后经过相距 27 m 的 A、B 两点所用时 间为 2 s,汽车经过 B 点时的速度为 15 m/s。求: (1)汽车经过 A 点时的速度大小; (2)汽车从出发点到 A 点的位移及平均速度大小。 答案:(1)12 m/s (2)48 m 6 m/s 解析:设汽车运动方向为正方向,则 vB=15 m/s,tAB=2 s,xAB=27 m

志鸿优化系列丛书 志鸿优化网,永远提供更新的: 丛书主编任志河。 http://www.zhyh.org IAn=2s Up=15 m/s AXA8-27 m B 匀加速直线 (I)设过A点时速度为yA,则AB段的平均速度 AB=0+卫=A+ug 2 2 故由XB=可AB MAB-VATVE4B 2 解得4=12m/s。 (2)对AB段: ag-4=l.5m/3 tAB 对OA段(o=0)月 由2-v02=2ar得 ko44a02-48m 2a 平均速度元0A=4e-6mS。 2 15.(12分)短跑运动员完成100m赛跑的过程可简化为匀加速运动和匀速运动两个阶段。一次比赛 中,某运动员用11.00s跑完全程。已知运动员在加速阶段的第2s内通过的距离为7.5m,求该运动员 的加速度及在加速阶段通过的距离。 答案5m/s210m 解析根据题意,在第1s和第2s内运动员都做匀加速运动。设运动员在匀加速阶段的加速度为α,在 第1s和第2s内通过的位移分别为x1和2,由运动学规律得 xi-zato2 ① xi+xz-a(2to) ② 式中0=1s。联立①②两式并代入已知条件,得 a=5 m/s2 ③ 设运动员做匀加速运动的时间为1,匀速运动的时间为2,匀速运动的速度为y跑完全程的时间为1全 程的距离为X。依题意及运动学规律,得 1=l1+l2 ④ v=at ⑤ x-zat:2+vh2 ⑥ 8
8 (1)设过 A 点时速度为 vA,则 AB 段的平均速度 𝑣𝐴𝐵 = 𝑣0 + 𝑣 2 = 𝑣𝐴 + 𝑣𝐵 2 故由 xAB=𝑣𝐴𝐵·tAB= 𝑣𝐴+𝑣𝐵 2 ·tAB 解得 vA=12 m/s。 (2)对 AB 段: a= 𝑣𝐵-𝑣𝐴 𝑡𝐴𝐵 =1.5 m/s2 对 OA 段(vO=0): 由 v 2 -𝑣0 2=2ax 得 xOA= 𝑣𝐴 2 -𝑣𝑂 2 2𝑎 =48 m 平均速度𝑣𝑂𝐴 = 𝑣𝐴+𝑣𝑂 2 =6 m/s。 15.(12 分)短跑运动员完成 100 m 赛跑的过程可简化为匀加速运动和匀速运动两个阶段。一次比赛 中,某运动员用 11.00 s 跑完全程。已知运动员在加速阶段的第 2 s 内通过的距离为 7.5 m,求该运动员 的加速度及在加速阶段通过的距离。 答案:5 m/s2 10 m 解析:根据题意,在第 1 s 和第 2 s 内运动员都做匀加速运动。设运动员在匀加速阶段的加速度为 a,在 第 1 s 和第 2 s 内通过的位移分别为 x1 和 x2,由运动学规律得 x1= 1 2 𝑎𝑡0 2 ① x1+x2= 1 2 a(2t0) 2 ② 式中 t0=1 s。联立①②两式并代入已知条件,得 a=5 m/s2 ③ 设运动员做匀加速运动的时间为 t1,匀速运动的时间为 t2,匀速运动的速度为 v;跑完全程的时间为 t,全 程的距离为 x。依题意及运动学规律,得 t=t1+t2 ④ v=at1 ⑤ x= 1 2 𝑎𝑡1 2+vt2 ⑥

志鸿优化系列丛书 志鸿优化网永远提供更新的! 丛书主编任志湖。 http://www.zhyh.org 设加速阶段通过的距离为x,则x之at2 ⑦ 联立③④⑤⑥⑦式,并代入数据得x'-10m。 ⑧ 16.(12分)如图所示,在公路的十字路口,红灯拦停了一车队,拦停的汽车排成笔直的一列,第一辆汽车 的前端刚好与路口停止线相齐,汽车长均为I=4.0m,前面汽车尾部与相邻汽车的前端相距均为 d山=1.0m。为了安全,前面汽车尾部与相邻汽车的前端相距至少为d=5.0m才能开动。若汽车都以 a=2ms2的加速度做匀加速直线运动,绿灯亮起瞬时,第一辆汽车立即开动。求: 停止线 (1)第六辆汽车前端刚到达停止线时的速度大小; (2)从绿灯刚亮起到第六辆汽车前端与停止线相齐所需最短时间1。 含案1)10ms(2)15s 解析1)第六辆汽车前端与停止线的距离 s1=5(l+d)=25.0m 由2-2aS1,得 v=√2as1=V2×2×25.0m/s=10m/s。 (2)设第二辆汽车刚开动时,第一辆汽车至少已行驶的时间为1,则第二辆汽车刚开动时,第一辆至少行 驶的距离 s2=d2-d=4.0 m 由at12得 -臣2s 从绿灯刚亮起到第六辆汽车刚开动至少所需时间 2=5l1=10s 第六辆汽车刚开动到前端与停止线相齐所需时间 6日-5s 从绿灯刚亮起到第六辆汽车前端与停止线相齐所需最短时间 1=2+3=15s。 9
9 设加速阶段通过的距离为 x',则 x'=1 2 𝑎𝑡1 2 ⑦ 联立③④⑤⑥⑦式,并代入数据得 x'=10 m。 ⑧ 16.(12 分)如图所示,在公路的十字路口,红灯拦停了一车队,拦停的汽车排成笔直的一列,第一辆汽车 的前端刚好与路口停止线相齐,汽车长均为 l=4.0 m,前面汽车尾部与相邻汽车的前端相距均为 d1=1.0 m。为了安全,前面汽车尾部与相邻汽车的前端相距至少为 d2=5.0 m 才能开动。若汽车都以 a=2 m/s2 的加速度做匀加速直线运动,绿灯亮起瞬时,第一辆汽车立即开动。求: (1)第六辆汽车前端刚到达停止线时的速度大小 v; (2)从绿灯刚亮起到第六辆汽车前端与停止线相齐所需最短时间 t。 答案:(1)10 m/s (2)15 s 解析:(1)第六辆汽车前端与停止线的距离 s1=5(l+d1)=25.0 m 由 v 2=2as1,得 v=√2𝑎𝑠1 = √2 × 2 × 25.0 m/s=10 m/s。 (2)设第二辆汽车刚开动时,第一辆汽车至少已行驶的时间为 t1,则第二辆汽车刚开动时,第一辆至少行 驶的距离 s2=d2-d1=4.0 m 由 s2= 1 2 𝑎𝑡1 2得 t1=√ 2𝑠2 𝑎 =2 s 从绿灯刚亮起到第六辆汽车刚开动至少所需时间 t2=5t1=10 s 第六辆汽车刚开动到前端与停止线相齐所需时间 t3= 𝑣 𝑎 =5 s 从绿灯刚亮起到第六辆汽车前端与停止线相齐所需最短时间 t=t2+t3=15 s