
§1.3条件概率 条件概率的概念 在解决许多概率问题时,往往需要在有某些附 加信息(条件)下求事件的概率 如在事件B发生的条件下求事件A发生的概率,将 此概率记作P(AB) 一般地P(AB)丰P(A) 1
在解决许多概率问题时,往往需要在有某些附 加信息 (条件 )下求事件的概率 . 如在事件 B发生的条件下求事件A发生的概率,将 此概率记作 P (A|B). 一般地 P (A|B) ≠ P (A ) §1.3 条件概率 条件概率的概念 1

例如,掷一颗均匀骰子,A={掷出2点}, B={掷出偶数点},P(A)=1/6,P(AB)=? 已知事件B发生,此时试验所有可能 结果构成的集合就是B, B中共有3个元素,它们的出现是等可 能的,其中只有1个在集A中.于是 P(AB)=1/3. 容易看到 P(AB)= 1/6 P(AB) 3/6 P(B) 2
P(A )=1/6, 例如,掷一颗均匀骰子,A={掷出2点}, B={掷出偶数点}, P(A|B)=? 已知事件B发生,此时试验所有可能 结果构成的集合就是B, P(A|B)= 1/3. B中共有3个元素,它们的出现是等可 能的,其中只有1个在集A中. 于是 容易看到 ( ) ( ) 3 6 1 6 3 1 P B P AB P(A|B) 2

又如,10件产品中有7件正品,3件次品,7件正品 中有3件一等品,4件二等品.现从这10件中任取一件, 记 A={取到一等品},B={取到正品} 则 P(A)=3/10, P; 3/10. P(AB) 7/10P(B) 3
又如,10件产品中有7件正品,3件次品,7件正品 中有3件一等品,4件二等品. 现从这10件中任取一件, 记 A={取到一等品},B={取到正品} P(A|B) ( ) ( ) 7 10 3 10 73 P B P AB 则 P(A )=3/10, 3

A={取到一等品},B={取到正品} P(A)=3/10, P(AB)=3/7 本例中,计算P(A)时,依据的前 提条件是10件产品中一等品的比例. 计算P(AB)时,这个前提条件未变,只是加上 “事件B已发生”这个新的条件. 这好象给了我们一个“情报”,使我们得以在某 个缩小了的范围内来考虑问题 4
P(A )=3/10, B={取到正品} P(A|B)=3/7 本例中,计算P(A)时,依据的前 提条件是10件产品中一等品的比例. A={取到一等品}, 计算P(A|B)时,这个前提条件未变,只是加上 “事件B已发生”这个新的条件. 这好象给了我们一个“情报”,使我们得以在某 个缩小了的范围内来考虑问题. 4
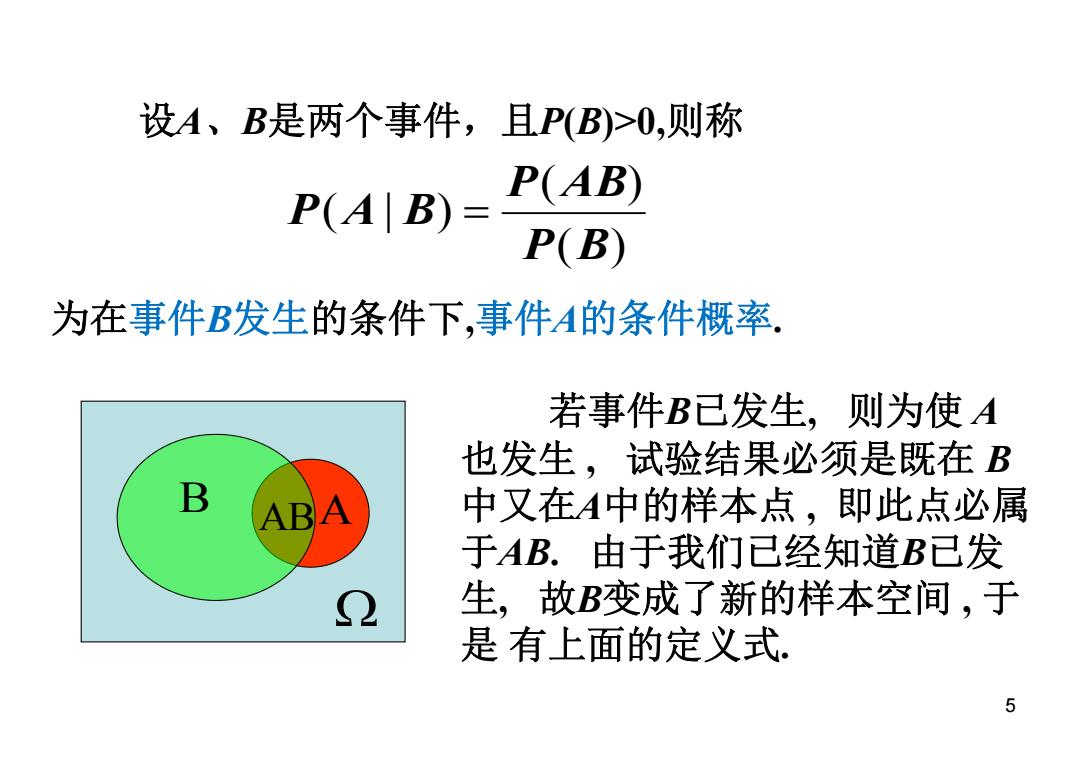
设A、B是两个事件,且P(B)>0,则称 P(A B)= P(AB) P(B) 为在事件B发生的条件下,事件A的条件概率. 若事件B已发生,则为使A 也发生,试验结果必须是既在B ABA 中又在A中的样本点,即此点必属 于AB.由于我们已经知道B已发 生,故B变成了新的样本空间,于 是有上面的定义式 5
若事件B已发生, 则为使 A 也发生 , 试验结果必须是既在 B 中又在A中的样本点 , 即此点必属 于AB. 由于我们已经知道B已发 生, 故B变成了新的样本空间 , 于 是 有上面的定义式. 设A、B是两个事件,且P(B)>0,则称 ( ) ( ) ( | ) P B P AB P A B B ABA 为在事件B发生的条件下,事件A的条件概率. 5

条件概率也是概率,故具有概率的性质: 口非负性 P(BA)≥0 规范性 P(2A)=1 可列可加性 aP(1A (B,B2,…两两互斥) a P(BB A)=P(B A)+P(B2 A)-P(BB2 A) 口P(BA)=1-P(BA) P(B-B2 A)=P(B A)-P(BB2 A) 6
条件概率也是概率, 故具有概率的性质: P ( B A ) 0 P ( A ) 1 1 i 1 i i P B i A P B A 非负性 规范性 可列可加性 1 2 1 2 12 P B B A P B A P B A P BB A ( ) ( )( )( ) P( )1 ( ) B A PB A 1 2 1 12 P( ) ( )( ) B B A P B A P BB A 6 1 2 ( 两两互斥) B B, ,

乘法公式 利用条件概率求积事件的概率即乘法公式 P(AB)=P(A)P(B A)(P(A)>0) P(AB)=P(B)P(A B)(P(B)>0) 推广 P(AA,…A)=P(A)PAA)…P(AnAA…An) (P(AA,…An)>0) 7
利用条件概率求积事件的概率即乘法公式 P ( A B ) P ( A ) P B A ( P ( A ) 0 ) P (AB ) P ( B ) P A B ( P ( B ) 0 ) 推广 ( ( ) 0 ) ( ) ( ) 1 2 1 1 2 1 2 1 1 2 1 n n n n P A A A P A A A P A P A A P A A A A 乘法公式 7

例 盒中装有5个产品,其中3个一等品,2个二 等品,从中不放回地取产品,每次1个,求: (1)取两次,两次都取得一等品的概率 (2) 取两次,第二次取得一等品的概率 : (3)取三次,第三次才取得一等品的概率; (4)取两次,已知第二次取得一等品,求: 第一次取得的是二等品的概率. 解:令A;为第1次取到一等品 32 P(A4)=PA)P(4A) 3 (1) 54 10 8
例 盒中装有5个产品, 其中3个一等品,2个二 等品, 从中不放回地取产品, 每次1个, 求: (1)取两次,两次都取得一等品的概率; (2)取两次,第二次取得一等品的概率; (3)取三次,第三次才取得一等品的概率; (4)取两次,已知第二次取得一等品,求: 第一次取得的是二等品的概率. 解: 令 A i 为第 i 次取到一等品 (1) 10 3 4 2 5 3 ( ) ( ) ( ) P A 1 A 2 P A 1 P A 2 A 1 8

(2)P(A)=P(A40AA)=P(A4)+P(A42) 2.3+3.2=3 54545 提问:第三次才取得一等品的概率,是 P(AAA2)还是P(AA2A)? (3)P(A 44)=P(A)P(A)P(444) 2131 二 54310 9
(3) 1 2 3 1 2 1 3 1 2 P(A A A ) P A P A A P A A A 10 1 3 3 4 1 5 2 提问:第三次才取得一等品的概率, 是 ( ) ( )? P A3 A1 A2 还是 P A1 A2 A3 ( ) ( ) ( ) ( ) (2) P A2 P A1A2 A1A2 P A1A2 P A1A2 5 3 4 2 5 3 4 3 5 2 9
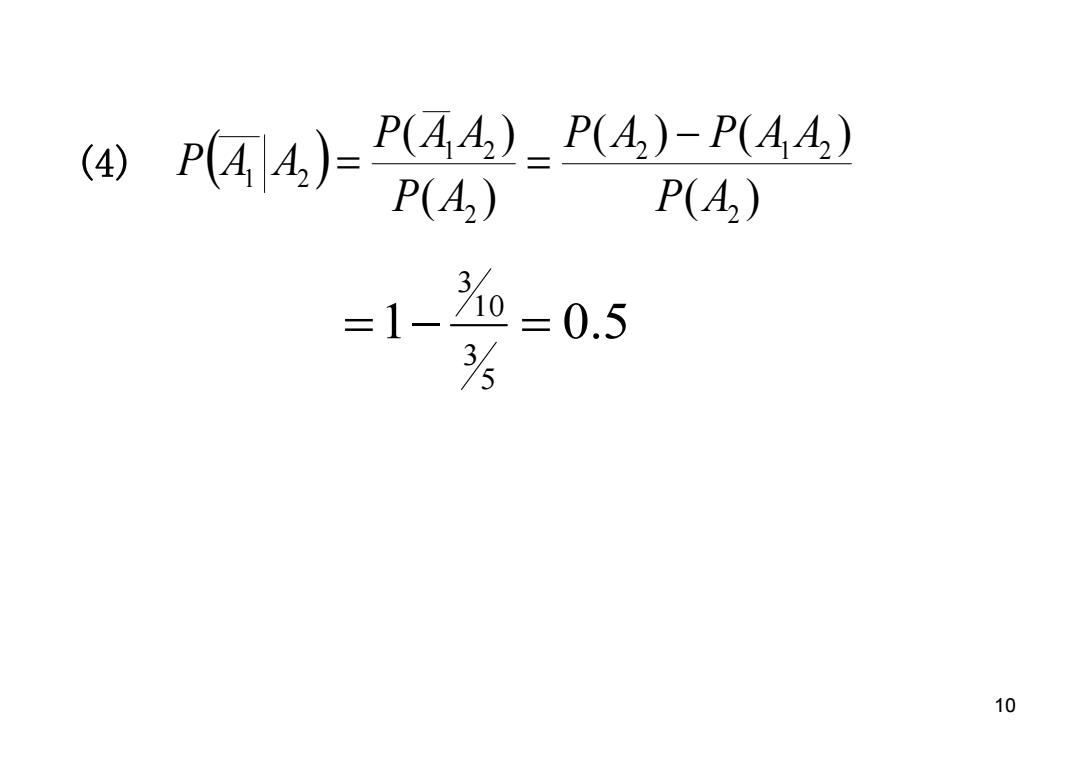
④P(44)=X-4P(44) P(A2) P(A2) 而 1、 =0.5 10
(4) ( ) ( ) ( ) ( ) ( ) 2 2 1 2 2 1 2 1 2 P A P A P A A P A P A A P A A 1 0.5 5 3 10 3 10