教案第七章气体动理论 第七章气体动理论Kinetics of Gas Molecules §1物质的微观模型统计规律性Statistical Regularity 分子运动论的基本概念与研究方法: 1.宏观物体是由大量分子或原子组成的,常温下的分子数密度量级为每立方厘米102个, 由于其线度在埃的量级,分子间的距离很大,一般为分子直径的10倍,故分子的大小可 略去不计,可以当作质点来处理。由于分子间的距离很大,故可以压缩,例如打气筒打 气,液体混合等。 2.分子在时刻不停地作无规则运动,但符合统计规律。 无规则运动间接验证为布朗运动一墨汁等颗粒在水中的无规则运动。 符合统计规律间接验证为加尔顿板。 3.分子间有相互作用力 分子间相互作用力的形式如左图,吸引例 ro-1A 子:光胶合。 光胶合:制造精密光学仪器时,把两个器件表 r-10A 面处理光滑、干净,加一定的压力即可能粘和 吸引力 在一起。 推斥力:固体和液体的难压缩性质,说明分子间存在 着一定的斥力。 粘合前 粘合后 115
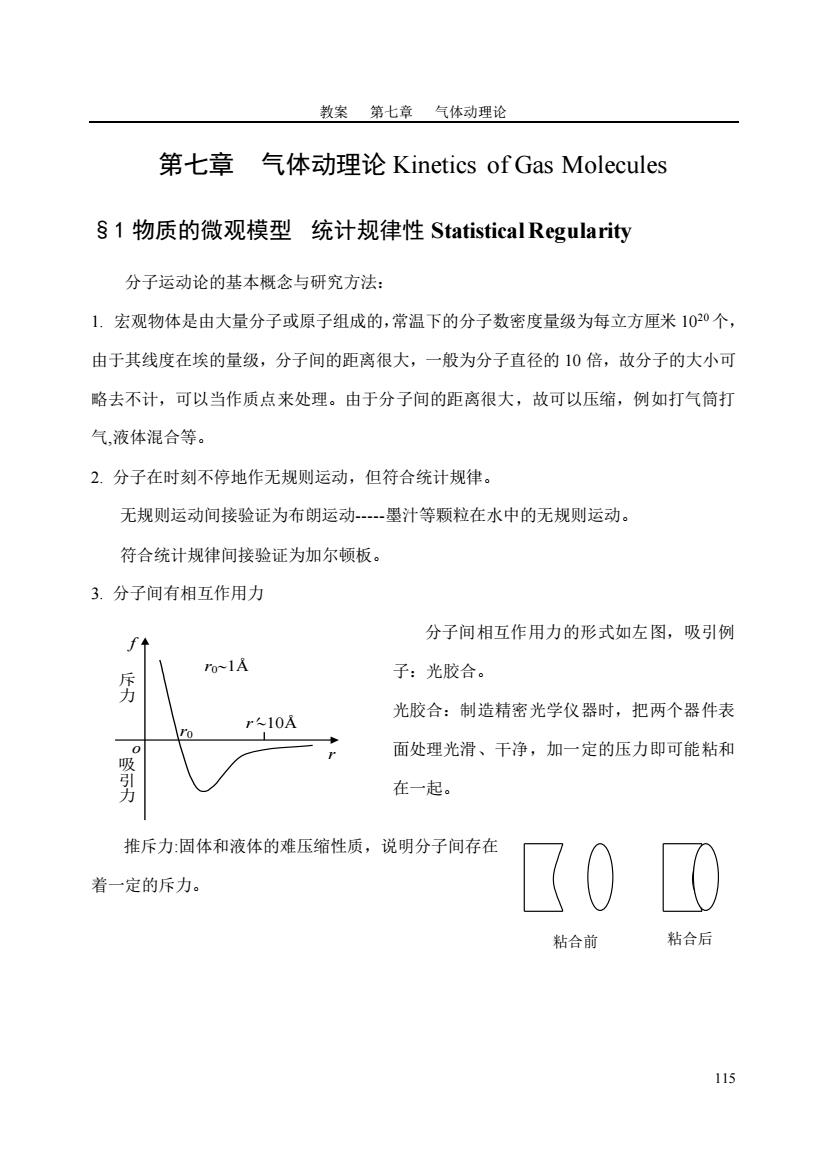
教案 第七章 气体动理论 115 第七章 气体动理论 Kinetics of Gas Molecules §1 物质的微观模型 统计规律性 Statistical Regularity 分子运动论的基本概念与研究方法: 1. 宏观物体是由大量分子或原子组成的,常温下的分子数密度量级为每立方厘米 1020 个, 由于其线度在埃的量级,分子间的距离很大,一般为分子直径的 10 倍,故分子的大小可 略去不计,可以当作质点来处理。由于分子间的距离很大,故可以压缩,例如打气筒打 气,液体混合等。 2. 分子在时刻不停地作无规则运动,但符合统计规律。 无规则运动间接验证为布朗运动-----墨汁等颗粒在水中的无规则运动。 符合统计规律间接验证为加尔顿板。 3. 分子间有相互作用力 分子间相互作用力的形式如左图,吸引例 子:光胶合。 光胶合:制造精密光学仪器时,把两个器件表 面处理光滑、干净,加一定的压力即可能粘和 在一起。 推斥力:固体和液体的难压缩性质,说明分子间存在 着一定的斥力。 r f 斥 力 吸 引 力 o r0 r01Å r10Å 粘合前 粘合后

教案第七章气体动理论 s2理想气体的压力公式The pressure formula ofideal gas 1.理想气体模型 1)分子可看作质点。客体:分子本占的大小与分子间距离比较可忽略 2)分子间相互作用力可忽略不计。客体:分子间平均距离很大(标准状态下约为分子有 效直径的10倍,即10左右),此时分子间作用力很小,只有碰撞时才有冲力作用。 根据理想气体模型,可有如下几条假设(推论也可): (1)同类气体分子的质量相等与速率无关。 (2)碰撞为完全弹性碰撞。 (3)热平衡时,分子沿各个方向的运动几率相等。 (4)容器不是很大时,忽略重力的影响。 2.理想气体压力公式的推导 说明:本节是以压力公式的推导为例,探讨气体分子运动论的研究问题的方法。因此, 重点讲解其方法的运用。(提炼模型的素质,简化问题的素质)。 气体压力是由于分子与器壁碰撞而产生的冲力。以A面为例进行研究:建立如图所 示的坐标系,设容器中共有N个相同的气体分子。一个分子与器壁发生一次完全弹性碰 撞的动量改变为: mU.(mUa)=2mvn:(只考虑大小,没计方向) 在单位时间内,分子与器壁的碰撞次数为: 2x :2红是分子在A,与A,间运动所需时间,则单位 时间内,器壁受到的力为: 6
教案 第七章 气体动理论 116 §2 理想气体的压力公式 The pressure formula of ideal gas 1. 理想气体模型 1)分子可看作质点。客体:分子本占的大小与分子间距离比较可忽略。 2)分子间相互作用力可忽略不计。客体:分子间平均距离很大(标准状态下约为分子有 效直径的 10 倍,即 10 左右),此时分子间作用力很小,只有碰撞时才有冲力作用。 根据理想气体模型,可有如下几条假设(推论也可): (1)同类气体分子的质量相等与速率无关。 (2)碰撞为完全弹性碰撞。 (3)热平衡时,分子沿各个方向的运动几率相等。 (4)容器不是很大时,忽略重力的影响。 2. 理想气体压力公式的推导 说明:本节是以压力公式的推导为例,探讨气体分子运动论的研究问题的方法。因此, 重点讲解其方法的运用。(提炼模型的素质,简化问题的素质)。 气体压力是由于分子与器壁碰撞而产生的冲力。以 A 1 面为例进行研究:建立如图所 示的坐标系,设容器中共有 N 个相同的气体分子。一个分子与器壁发生一次完全弹性碰 撞的动量改变为: m ix -(-m ix )=2 m ix ;(只考虑大小,没计方向) 在单位时间内,分子与器壁的碰撞次数为: x x 2 ; x x 2 是分子在 A 1 与 A 2 间运动所需时间,则单位 时间内,器壁受到的力为: x y z z y A1 A2 o x -mvx mvx v

教案第七章气体动理论 2mu2m2+中2mue会 2x -u+u++ue p=E.m(w2+叶ua2++u =Nwu.2++2++ueW 2 =n'm.v2 0F=0+0+0☑ 而v2=v2=v2(几率相等) G=m0为分子的平均平动动能 3.压力公式的物理意义 1)P正比于n和.是一个统计量,只对大量气体分子适用 2)把宏观量和微观量联系在一起了。 说明:因为微观量不能测量,故不能直接用实验来检验其正确性,但从此公式出发,可 以满意的解释或论证已经过实验检验的气体诸定律。 例题1:球形器壁内压强公式的推导。 解:如图,设碰撞为完全弹性碰撞矮子每次碰撞中,分 子作用于器壁的法向冲量为:2mU,Cos0:单位时间内 2 U 的隧撞次数为:2心0:则每秒作用于器壁的冲量 N个分子 117
教案 第七章 气体动理论 117 F=2 m 1x x x 2 1 + • • •+2 m ix x ix 2 + • • •+2 m Nx x Nx 2 = x m ( 2 1x + • • •+ 2 ix + • • •+ 2 Nx ) P= yz F = xyz m ( 2 1x + • • •+ 2 ix + • • •+ 2 Nx ) = xyz N •M•( 2 1x + • • •+ 2 ix + • • •+ 2 Nx )/N =n •m • 2 x 2 = 2 x + 2 y + 2 z = 3 1 n m 2 而 2 x = 2 y = 2 z (几率相等) = 3 2 n ( 2 1 m 2 ) = 3 2 n = 2 1 m 2 :为分子的平均平动动能. 3. 压力公式的物理意义 1)P 正比于 n 和 .是一个统计量,只对大量气体分子适用。 2)把宏观量和微观量联系在一起了。 说明:因为微观量不能测量,故不能直接用实验来检验其正确性,但从此公式出发,可 以满意的解释或论证已经过实验检验的气体诸定律。 例题 1:球形器壁内压强公式的推导。 解:如图,设碰撞为完全弹性碰撞矮子每次碰撞中,分 子作用于器壁的法向冲量为:2m i Cos ;单位时间内 的碰撞次数为: RCos i 2 ;则每秒作用于器壁的冲量 vi vi R O 2Rcos N 个分子

教案第七章气体动理论 U,_m心 为(一个气体分子):加u0s02RCg发:番壁每秒受到的总冲量为: 压强号贤4- R 34 m 即:球形器壁内压强公式与立方形的完全相同,对其他形状的器壁与完全是同样的结论, 因为此较复杂,这里就不一一证明了。 问:如是任意形状容器,从理论上讲怎样证明?(采用卡诺定理的证明方法,用无限多 个方形和球形容器代替。) §3气体分子的平均平动动能与温度的关系The temperature formula ofideal gas 在PV=MT中:设分子质量为,分子数为N,则有: N N。m 光是mT (1) 中为分子度:是180为尔发侧 常数:N为阿伏伽德罗常数(Avogadto)): 而 (2) 118
教案 第七章 气体动理论 118 为(一个气体分子):2m i Cos RCos i 2 = R m i 2 ;器壁每秒受到的总冲量为 : = N i 1 R m i 2 = R m = N i i 1 2 ; 压强 P= S F =( R m = N i i 1 2 )/4 2 R = 3 1 3 3 4 R N m N N i i =1 2 = 3 1 n m 2 即:球形器壁内压强公式与立方形的完全相同,对其他形状的器壁与完全是同样的结论, 因为比较复杂,这里就不一一证明了。 问:如是任意形状容器,从理论上讲怎样证明?(采用卡诺定理的证明方法,用无限多 个方形和球形容器代替。) §3 气体分子的平均平动动能与温度的关系 The temperature formula of ideal gas 在 PV= M RT 中:设分子质量为 m,分子数为 N,则有: PV= N m Nm 0 RT= N0 N RT P= N0 N V RT = V N N0 R T=n k T (1) 其中 n= V N 为分子数密度;k= N0 R = 23 6.02 10 8.31 =1.38 10 −23 J•k −1 为玻尔兹曼(Boltzmann) 常数;N0 为阿伏伽德罗常数(Avogadto); 而 P= 3 2 n (2)

教案第七章气体动理论 由(1),(2)得: 9 说明T=0是不可能的(量子理论观点既运动是绝对的)。 此处加入方均根速率:V厅:3产。,7 μVm (③)式说明:温度是表征大量气体分子热运动激烈程度的物理量,平均平动动能与温度成 正比。同压力一样,温度也是一个统计量。 量级的概念:当T=300k时,8=102'J相当之小。 §4能量均分定理.理想气体内能Equilibration Theorem of Energy,The internal energy ofideal gas 1.自由度 决定一物体的空间位置所需要的独立坐标数目。一个在空间自由运动的质点,自由 度为3.(xy,z,=3一个刚性双原子分子自由度为5(x,y,Z,a,0,=5:因为三个角度中 只有两个是独立的。 2.能量按自由度均分定理 单原子理想气体的平均平动动能为:石=k虹,单原子气体分子有三个自由度,而气 体分子在各个方向上的运动几率相等,故有: 21 即:在平衡状态时,理想气体分子的每个自由度都具有大小等于)kT的能量,这个定理 叫做能量按自由度均分定理。 119
教案 第七章 气体动理论 119 由(1),(2)得: = 2 3 kT (3) 说明 T=0 是不可能的(量子理论观点既运动是绝对的)。 此处加入方均根速率: 2 = 3RT = m 3kT (3)式说明:温度是表征大量气体分子热运动激烈程度的物理量,平均平动动能与温度成 正比。同压力一样,温度也是一个统计量。 量级的概念:当 T=300k 时, =10 −21 J 相当之小。 §4 能量均分定理.理想气体内能 Equilibration Theorem of Energy,The internal energy of ideal gas 1. 自由度 决定一物体的空间位置所需要的独立坐标数目。一个在空间自由运动的质点,自由 度为 3.(x,y,z),i=3 一个刚性双原子分子自由度为 5(x,y,z,,),i=5:因为三个角度中 只有两个是独立的。 2. 能量按自由度均分定理 单原子理想气体的平均平动动能为: = 2 3 kT,单原子气体分子有三个自由度,而气 体分子在各个方向上的运动几率相等,故有: 2 1 m 2 x = 2 1 m 2 y = 2 1 m 2 z = 2 1 k T 即:在平衡状态时,理想气体分子的每个自由度都具有大小等于 2 1 k T 的能量,这个定理 叫做能量按自由度均分定理

教案第七章气体动理论 对于双原子分子,自由度5,则,-k下k下平均平动动能(D+平均转动 动能(k)。多原子分子的自由度要复杂些,这里不进行讨论,一般6。 一个刚性双原子的动能可写为如下的形式: (1) 在温度为T的平衡状态下,气体分子按能量分布遵循玻而兹曼分布律:N。xa:a 为一与速度,角速度无关的常数,处在e附近dv,d心,dD,do,d@,范围内的分子数 为: dN,-e%dv,dv,dv,do,do, 显然: se dv,dv,dv,do,do,-N 现以10:为例,计算方向的平均转动动能: 5a-上es次u,u,dw.a,do, =上ae°a加上-上o:亩mndu,d,dw do, 利用分部积分司:上:高a,号益, 代入上式可得: kT 1 是o--上7 ,dv,,u.dado,-K灯 同理可证: 2mu2=1 u-mu--k灯 120
教案 第七章 气体动理论 120 对于双原子分子,自由度 i=5,则 a = 2 i k T= 2 5 k T=平均平动动能( 2 3 k T)+平均转动 动能( 2 2 k T)。多原子分子的自由度要复杂些,这里不进行讨论,一般 i=6。 一个刚性双原子的动能可写为如下的形式: = 2 1 m 2 x + 2 1 m 2 y + 2 1 m 2 z + 2 2 1 x I + 2 2 1 y I (1) 在温度为 T 的平衡状态下,气体分子按能量分布遵循玻而兹曼分布律:N ae KT − ;a 为一与速度,角速度无关的常数,处在 附近 d x d y d z d x d y 范围内的分子数 为: d N = ae KT − d x d y d z d x d y 显然: − − ae KT − d x d y d z d x d y =N 现以 2 2 1 x I 为例,计算方向的平均转动动能: 2 2 1 x I = N 1 − − 2 2 1 x I ae KT − d x d y d z d x d y = N 1 − − x KT I I x e d x 2 2 2 2 1 − − 2 2 1 x I ae ( ) 2 1 2 2 2 2 x y z y m m m I kT − + + + d x d y d z d y 利用分部积分可得: − − x KT I I x e d x 2 2 2 2 1 = 2 kT − x KT I e d x 2 2 代入上式可得: 2 2 1 x I = − − 2 kT N 1 ae KT − d x d y d z d x d y = 2 1 KT 同理可证: 2 2 1 m x = 2 2 1 m y = 2 2 1 m z = 2 2 1 y I = 2 1 KT

教案第七章气体动理论】 这说明:大量气体分子处在平衡状态下,在各个自由度上占有相同的平均能量。 kro,k器0 Kdo, 3.理想气体的内能 理想气体分子之间无相互作用势,因此,一摩尔理想气体的内能为E=。6。= 义灯红对报为的气体关为为E业名c,工关种c一 称为理想气体的等容摩尔热容。上式说明:对一定质量的理想气体,其内能反由自由度 和温度来决定,既理想气体的内能只是温度的单值函数。 4.固体热容 圆休热容定义为:C=号 当温度发生变化时,对固体而言,压强、体积变化非常小,故不区别定体热从和定压热 容。 下面分析固体的摩尔热容,组成固体的N个原子在固体中的运动为在晶格附近的热振动, 这个振动是三维的,我们把每个原子的三维振动看作是一个维振了,对每个原子的一维 121
教案 第七章 气体动理论 121 这说明:大量气体分子处在平衡状态下,在各个自由度上占有相同的平均能量。 注: − − x KT I I x e d x 2 2 2 2 1 = − − KT I x x I de 2 2 2 2 1 (- I 2KT ) x 2 1 = − 2 1 KT − KT I x x de 2 2 () = − 2 1 KT( − − KT I x x e 2 2 − − − x KT I e d x 2 2 ) = 2 1 KT − − x KT I e d x 2 2 − − KT I x x e 2 2 =2 KT I e 2 2 − =0 3. 理想气体的内能 理想气体分子之间无相互作用势,因此,一摩尔理想气体的内能为 E=N 0 a = N 0 2 i KT= 2 i RT 对质量为 m 的理想气体,其内能为:E= M 2 i RT= M C v T;其中 C v = 2 i R 称为理想气体的等容摩尔热容。上式说明:对一定质量的理想气体,其内能反由自由度 和温度来决定,既理想气体的内能只是温度的单值函数。 4. 固体热容 固体热容定义为: dT dQ C = 当温度发生变化时,对固体而言,压强、体积变化非常小,故不区别定体热从和定压热 容。 下面分析固体的摩尔热容,组成固体的 N 个原子在固体中的运动为在晶格附近的热振动, 这个振动是三维的,我们把每个原子的三维振动看作是一个维振了,对每个原子的一维

教案第七章气体动理论 振动,有质心坐标和相对质心的质点坐标两个自由度,即1,则每个原子的振动能量为: E=3x2x-KT=3KT 1mol品体的振动能量为: E=N &=3N kT=3RT 其摩尔热容为:C-号=票=识25nar 即理想晶体的摩尔热容是不依赖于温度的常量,上式称为杜隆珀蒂定律,是他们于1819 年在实验中发现的此规律,下面给出几种固体的摩尔热容值。 铝铜镉金铂银锡 (20℃) 25.724.725.626.626.325.727.8Cm(Jmo1.kl) 当温度不太低时,杜隆珀蒂定律与实验值符合的很好,当温度很低时,固体的摩尔热容 明显地依赖于温度,此时,能量均分定理则解释不了,而需要用量子理论来解决。下图 为银的摩尔热容与温度曲线。 s5麦克斯韦分子速率分布律Max well Velocity Distribution 处于平衡态的气体分子,以不同的速率沿着各个方向运动着,有的分子速率较大,有 的较小由于相互碰撞,每个分子的速率都在不断的改变因此,个别分子的运动完全是偶 然的。然而从大量分子整体来看,在一定条件下,分子的速率分布遵从着一定的统计规 律。1895年,英国物理学家从理论上得到了这一规律。 注:麦克斯韦(英国)与1859年导出分布律,由0.Stern于1920年用实验证实其正确 性。麦克斯韦还建立了经典电磁理论,并预言电磁波的存在,后由赫兹由实验验证。 具体实验是如下进行的(O.Stern1888-1969): 1.测定气体分子速率的实验 122
教案 第七章 气体动理论 122 振动,有质心坐标和相对质心的质点坐标两个自由度,即 i=1,则每个原子的振动能量为: KT 3KT 2 1 = 3 2 = 1mol 晶体的振动能量为: E = NA = 3NA kT = 3RT 其摩尔热容为: 1 1 3 25 − − = = = R = J mol l dT dE dT dQ Cm 即理想晶体的摩尔热容是不依赖于温度的常量,上式称为杜隆-珀蒂定律,是他们于 1819 年在实验中发现的此规律,下面给出几种固体的摩尔热容值。 铝 铜 镉 金 铂 银 锡 (20℃) 25.7 24.7 25.6 26.6 26.3 25.7 27.8 Cm(Jmol-1 k -1 ) 当温度不太低时,杜隆-珀蒂定律与实验值符合的很好,当温度很低时,固体的摩尔热容 明显地依赖于温度,此时,能量均分定理则解释不了,而需要用量子理论来解决。下图 为银的摩尔热容与温度曲线。 §5 麦克斯韦分子速率分布律 Maxwell Velocity Distribution 处于平衡态的气体分子,以不同的速率沿着各个方向运动着,有的分子速率较大,有 的较小.由于相互碰撞,每个分子的速率都在不断的改变.因此,个别分子的运动完全是偶 然的。然而从大量分子整体来看,在一定条件下,分子的速率分布遵从着一定的统计规 律。1895 年,英国物理学家从理论上得到了这一规律。 注: 麦克斯韦(英国)与 1859 年导出分布律,由 O.Stern 于 1920 年用实验证实其正确 性。 麦克斯韦还建立了经典电磁理论,并预言电磁波的存在,后由赫兹由实验验证。 具体实验是如下进行的(O.Stern 1888-1969): 1. 测定气体分子速率的实验

教案第七章气体动理论 莽汽 测定气体分子速率的实验装置 (斯特思0.Stern,1920年): 图中A是产生金属蒸汽分子的汞气源汞气由电炉加热汞而获得。汞汽分子通过狭缝 S后,形成一条很窄的分子射线B和C是相距为的两个共轴圆盘,两狭缝的夹角日约为 2°左右。D是接受汞气分子的显示屏。(1921年,0.Siem和W.Gerlsch又做了解均匀磁 场中S态原子射线来分裂的实验,导致了1925年G.E.Uhlenbeck和S.A.Goudsmit提出电 子自旋的概念)当B、C以转动时,并设通过的B分子全能通过C只有满足下列关系 的分子才能通过C即: 或: v o =21 (1) 考虑到狭缝有一定的宽度,实际上当0一定时,解得到D上的分子是速率在v~v+ △v之间的分子。 当0不同时,可测得D上沉积的金属层的厚度对应着不同速率间内的分子数。比较 这些厚度,即可知道在y~y+△ N△Y v,2~2+△v之间的相对分子数。 左图是在100C时,汞分子的速率分布 123 求分子速率分布情况
教案 第七章 气体动理论 123 (斯特恩 O.Stern,1920 年): 图中 A 是产生金属蒸汽分子的汞气源.汞气由电炉加热汞而获得。汞汽分子通过狭缝 S 后,形成一条很窄的分子射线.B 和 C 是相距为的两个共轴圆盘,两狭缝的夹角 约为 2 0 左右。D 是接受汞气分子的显示屏。(1921 年,O.Stern 和 W.Gerlsch 又做了解均匀磁 场中 S 态原子射线来分裂的实验,导致了 1925 年 G.E.Uhlenbeck 和 S.A.Goudsmit 提出电 子自旋的概念)当 B、C 以转动时,并设通过的 B 分子全能通过 C 只有满足下列关系 的分子才能通过 C.即: = v l ; 或: v = l (1) 考虑到狭缝有一定的宽度,实际上当 一定时,解得到 D 上的分子是速率在 v v + Δ v 之间的分子。 当 不同时,可测得 D 上沉积的金属层的厚度.对应着不同速率间内的分子数。比较 这些厚度,即可知道在 1 v 1 v + Δ v , 2 v 2 v +Δ v 之间的相对分子数。 左图是在 100℃时,汞分子的速率分布 Hg l A B C S D 蒸汽 测定气体分子速率的实验装置 v N v N 求分子速率分布情况

教案第七章气体动理论 曲线。 说明:1930-1934年蔡特曼(zartman)与我国物理学家葛正权对stern实验进行了改进, (见教材P260)。实验结果很好,改进的装置无须调即可得到不同的v。 2.麦克斯韦气体分子速率分布定律: 定义速率分布函数: m=典然典-员器 、△N_1dW 或 N=f(v)dv dN (1) )物理意义:气体分子在速率附近处于单位速率间隔的几率,也叫几奉密度。 理论上给出)的形式为:若在直角坐标系中,则为: -(0答 e (2) 自化条作为【0h=1口即 =1(玻耳兹曼分布律中要用到) (1)可写为: 0rh (3) (3)式给出理想气体处于平衡态时,分布在一+v的相对分子数,这个分布规律叫 marwell速率分布律。 这个规律与实验符合的很好,是 分子运动论的基本规律之一。图中的 矩形面积表示在速率区间→叶d的 相对分子数,如果速率区间取得越小, 124 )与v的关系曲线
教案 第七章 气体动理论 124 曲线。 说明:1930-1934 年蔡特曼(zartman)与我国物理学家葛正权对 stern 实验进行了改进, (见教材 P260)。实验结果很好,改进的装置无须调即可得到不同的 v。 2. 麦克斯韦气体分子速率分布定律: 定义速率分布函数: dv dN v N N N v N N f v v v 1 lim 1 ( ) lim 0 0 = = = → → 或 f v dv N dN = ( ) (1) f(v)物理意义:气体分子在速率附近处于单位速率间隔的几率,也叫几率密度。 理论上给出 f(v)的形式为:若在直角坐标系中,则为: ( ) KT m v v v x y z x y z e KT m f v v v 2 3 2 2 2 2 2 ( ) + + − = 、 、 2 2 3 2 2 2 ( ) 4 e v KT m f v KT mv = − (2) 归一化条件为: = ( ) 1 0 f v dv 即 1 0 = N dN (玻耳兹曼分布律中要用到) (1)可写为: e v dv KT m N dN KT mv 2 2 3 2 2 2 4 − = (3) (3)式给出理想气体处于平衡态时,分布在 v—v+dv 的相对分子数,这个分布规律叫 marwell 速率分布律。 这个规律与实验符合的很好,是 分子运动论的基本规律之一。图中的 矩形面积表示在速率区间 v→v+dv 的 相对分子数,如果速率区间取得越小, f(v) v v o vp f(v)与 v 的关系曲线