
教案第十一章稳恒磁场 第十一章稳恒磁场Steady Magnetic Field s1磁场、磁感应强度Magnetic Field,Magnetic Induction 人类发现磁现象要比发现电现象早得多,这是因为自然界中有很多磁现象,如磁石 (©;O4)能够吸引铁屑的现象等等。利用地磁的存在制造的指南针在11世纪初就已经在我 国的航海上有了应用。自然界这些磁现象的发现和应用,激励着人们去进一步探索其内 在的规律,挖掘新的应用价值。 我们知道,静止的电荷之间有相互作用,而这相互作用是通过电场来传递的。那么 电流之间,也就是运动的电荷之间有无相互作用呢?如果存在相互作用,它是靠什么来 传递的呢?实验发现,电流之间的相互作用是由磁场来传递的。磁场是一种物质,并且 对在磁场中的运动电荷有作用力。 根据运动电荷在磁场中的实验,可以观察到以下实验现象: 1作用于运动电荷上的磁力F,其方向与运动电荷的速度垂直。即F⊥下。 2作用力与电荷电量q和运动速率v成正比,即F文q:FcV: 3作用力的大小与速度下与磁感应强度B的夹角有关,当B∥下时,F=0:当 B⊥下时,F最大。 根据以上实验结果,定义磁感应强度B的大小和方向如下: 1方向:正电荷的运动方向与磁场中磁针N相指向相同时,磁力为零,规定这个方 向为磁感应强度B的方向。 2大小:当正电荷在磁场中某点的速度下与B垂直时,它所受的磁力F最大,规定 该点磁感应强度大小为: B=F qv B的国际单位为:特斯拉(T 根据前面的实验现象可知,磁力F既与B垂直,也与下垂直,且构成右手螺旋关系
教案 第十一章 稳恒磁场 180 第十一章 稳恒磁场 Steady Magnetic Field §1 磁场、磁感应强度 Magnetic Field, Magnetic Induction 人类发现磁现象要比发现电现象早得多,这是因为自然界中有很多磁现象,如磁石 (Fe3O4)能够吸引铁屑的现象等等。利用地磁的存在制造的指南针在 11 世纪初就已经在我 国的航海上有了应用。自然界这些磁现象的发现和应用,激励着人们去进一步探索其内 在的规律,挖掘新的应用价值。 我们知道,静止的电荷之间有相互作用,而这相互作用是通过电场来传递的。那么 电流之间,也就是运动的电荷之间有无相互作用呢?如果存在相互作用,它是靠什么来 传递的呢?实验发现,电流之间的相互作用是由磁场来传递的。磁场是一种物质,并且 对在磁场中的运动电荷有作用力。 根据运动电荷在磁场中的实验,可以观察到以下实验现象: 1 作用于运动电荷上的磁力 F,其方向与运动电荷的速度垂直。即 F v ⊥ 。 2 作用力与电荷电量 q 和运动速率 v 成正比,即 F q ; F v ; 3 作用力的大小与速度 v 与磁感应强度 B 的夹角有关,当 B v // 时, F = 0 ;当 B v ⊥ 时, F 最大。 根据以上实验结果,定义磁感应强度 B 的大小和方向如下: 1 方向:正电荷的运动方向与磁场中磁针 N 相指向相同时,磁力为零,规定这个方 向为磁感应强度 B 的方向。 2 大小:当正电荷在磁场中某点的速度 v 与 B 垂直时,它所受的磁力 F⊥最大,规定 该点磁感应强度大小为: qv F B ⊥ = B 的国际单位为:特斯拉(T) 根据前面的实验现象可知,磁力 F 既与 B 垂直,也与 v 垂直,且构成右手螺旋关系

教案第十一章稳恒磁场 它们之间的矢量关系可写成 F=qvxB 像电场中一样,磁场也分为均匀磁场和非均匀磁场。 说明:磁感强度B也可由实验线圈在磁场中所受的磁矩来规定。 B=M达,其中Pm为实验线圈的磁矩。M为实验线圈所受到的最大磁力矩,B 的方向为线圈处于平衡位置时线圈磁矩的方向。 下面给出自然界中磁场大小的近似值。 人体磁场:1012T 地球两极附近:6×10T 大型电磁铁:1-2T 超导电磁铁:5-40T 因为特斯近这个单位太大,人们还习惯于用高斯单位制中的高斯来表示,其关系如 1特斯拉(T①=10高斯(G) §2毕奥一萨伐尔定律Biot-savart law 毕奥一萨伐尔定律是一条实验定律。根据毕奥和萨伐尔两人的实验结果,拉普拉斯 从数学上推出了其数学表达式,故此定律又称毕奥一萨伐尔一拉普 拉斯定律。它从数学上给出了一个电流元d在空间下处产生的磁 感应强度dB为: dB=Ho ldlx 4π 根据迭加原理,一个任意载流导线在场点严处产生的 磁感应强度为: -时绘 B 下面根据毕奥一萨伐尔定律求个典型电流的磁场。 181
教案 第十一章 稳恒磁场 181 它们之间的矢量关系可写成 F qv B = 像电场中一样,磁场也分为均匀磁场和非均匀磁场。 说明:磁感强度 B 也可由实验线圈在磁场中所受的磁矩来规定。 Pm M B 最大 = ,其中 Pm 为实验线圈的磁矩。M 最大为实验线圈所受到的最大磁力矩, B 的方向为线圈处于平衡位置时线圈磁矩的方向。 下面给出自然界中磁场大小的近似值。 人体磁场:10-12T 地球两极附近:610-5T 大型电磁铁:1-2T 超导电磁铁:5-40T 因为特斯近这个单位太大,人们还习惯于用高斯单位制中的高斯来表示,其关系如 下: 1 特斯拉(T)=104 高斯(G) §2 毕奥-萨伐尔定律 Biot-savart law 毕奥-萨伐尔定律是一条实验定律。根据毕奥和萨伐尔两人的实验结果,拉普拉斯 从数学上推出了其数学表达式,故此定律又称毕奥-萨伐尔-拉普 拉斯定律。它从数学上给出了一个电流元 Idl 在空间 r 处产生的磁 感应强度 dB 为: 3 0 4 r Idl r dB = 根据迭加原理,一个任意载流导线在场点 r 处产生的 磁感应强度为: 3 0 4 r Idl r B dB = = 下面根据毕奥-萨伐尔定律求 n 个典型电流的磁场。 dB Idl r P I Idl r O P B a

教案第十一章稳恒磁场 载流长直导线的磁场: 设图中P点到长直导线的垂直距离为a,取电流元Id,则电流元在P点产生的感应 强度为: dB=to ldisin ;方向如图 4n r2 BHoldlsin 4πJr2 积分上式即可求得B。 根据图中几何关系有: sBncos:I=a y=-a 故有:dl=a ”c03后代入积分表达式中可得 dB B=Holf cadp 装nA-广m a2 结4-m (1) 注意:图中B1、B2是如何取值的,角的取法不同,表达式是不一样的,这点要特别 注意,若按下图来取角度,则表达式为: B=sg-aa)a 讨论:若导线为无限长载流直导线,在()式中有: A=月 A=受:B= 2πa 在2)试中,8=0,8,=π:B= 2πa
教案 第十一章 稳恒磁场 182 载流长直导线的磁场: 设图中 P 点到长直导线的垂直距离为 a,取电流元 Idl ,则电流元在 P 点产生的感应 强度为: 2 0 sin 4 r Idl dB = ;方向如图 = 2 0 sin 4 r I dl B 积分上式即可求得 B。 根据图中几何关系有: cos = sin = cos ; l = tg 故有: 2 cos d dl = 代入积分表达式中可得 ( ) 2 1 0 0 2 2 2 0 sin sin 4 cos 4 cos cos 4 cos 2 1 2 1 = − = = I d I d I B (1) 注意:图中1、2 是如何取值的,角的取法不同,表达式是不一样的,这点要特别 注意,若按下图来取角度,则表达式为: ( ) 1 2 0 cos cos 4 = − I B (2) 讨论:若导线为无限长载流直导线,在(1)式中有: 2 1 = − 2 2 = ; 2 0 I B = 在(2)式中, 1 = 0 , 2 = ; 2 0 I B = I Idl r O P a

教案第十一章稳恒磁场 即无限长载流直导线的B是在同一圆周上大小相等的,方向沿切线方向。 圆形载流导线的磁场 在圆周上取电流元1d,根据毕 奥一萨伐尔定律得: dB=Ho ldll 47子(此处090 把dB分解为垂直于x轴的dBL 和在x轴方向的dB/。根据对称性可知,所有电流元产生的BL分量互相抵消,最后磁 场只有沿x轴方向的分量,故有: 8--s-会兽mp=可会8 4πr -绘u-会2成- 4R2 4πr3 2r3 26r2+R2严 讨论: 1)我流圆环中心处磁场:X0。B=方向沿x轴正向,B与了的方向满足右手螺 2R 旋关系,这是安培分子电流假说的模型。 其中S=πR为圆线圈面积。M=S为圆线圈磁矩,方向取S的法线方同。 m=尽对任何形状的线圈都适用。 载流螺线管的磁场 长为1、半径为R、总匝数为N、流有电 流1的长直螺线管,求管内轴线上任一点的 磁感应强度。 解:取轴线上P点为坐标原点(O),P点 x2O(P) 的磁场可视为无限多个宽度为k的圆电流 产生的迭加场,对厚度为dx的圆电流有: ---- 183
教案 第十一章 稳恒磁场 183 即无限长载流直导线的 B 是在同一圆周上大小相等的,方向沿切线方向。 圆形载流导线的磁场 在圆周上取电流元 Idl ,根据毕 奥-萨伐尔定律得: 2 0 4 r Idl dB = (∵此处=90) 把 dB 分解为垂直于 x 轴的 dB⊥ 和在 x 轴方向的 dB//。根据对称性可知,所有电流元产生的 dB⊥分量互相抵消,最后磁 场只有沿 x 轴方向的分量,故有: ( ) 3 2 2 2 2 0 3 2 0 3 0 3 0 3 0 2 0 / / 2 2 2 4 4 4 sin 4 sin x R IR r IR R r R dl r R dl r R r Idl B dB dB + = = = = = = = = 讨论: 1)载流圆环中心处磁场:x=0, R I B 2 0 = 方向沿 x 轴正向, B 与 I 的方向满足右手螺 旋关系,这是安培分子电流假说的模型。 2)在远离原点的轴线上:x>>R; 3 0 3 0 3 2 0 2 2 2 x m x IS x IR B = = = 其中 S=R 2 为圆线圈面积。M=IS 为圆线圈磁矩,方向取 S 的法线方同。 m IS = 对任何形状的线圈都适用。 载流螺线管的磁场 长为 l、半径为 R、总匝数为 N、流有电 流 I 的长直螺线管,求管内轴线上任一点的 磁感应强度。 解:取轴线上 P 点为坐标原点(0),P 点 的磁场可视为无限多个宽度为 dx 的圆电流 产生的迭加场,对厚度为 dx 的圆电流有: x x P r I Idl O R dB ┴ dB dB/ / dx x2 x1 x O(P)

教案第十一章稳恒磁场 山-兰=h:M为单位长度的面数 dB=Lo RiIndx 2(R2+x2 8=可西R R'dx 为便于积分,用那代替x, x=RCIgB,(x+R2)=R2(1+ctg'B)=R2csC2B dx =-Rcsc2 BdB B受婴警-受广如 即:B=-,(eosR,-cosR) 注意:B1、B2的几何意义(即取法) 讨论:1)轴线上的中点:此时B,=π-B2;cosB=-cosB2而 112 cosβ2= V0/2}+R2 则B=4nlc0sA,=4 2P14+R严:若P>R:即无 限长的,则B=2=4l,管内磁场是均匀的。 2)若P点处于半无限长螺线管的一端,即 A=子及=0政月=,民=2, 则B=24l 3)长直螺线管内轴线上的磁感应分布如下图所 示,中部附近的磁场完全可视为均匀磁场。 运动电荷的磁场: 因电流是由自由电子定向运动形成的,可以认为电流所激发的磁场其实是由运动电 ®
教案 第十一章 稳恒磁场 184 dx Indx l NI dI = = ;n=N/l 为单位长度的匝数。 ( ) 3 2 2 2 2 0 2 R x R Indx dB + = ( ) + = = 2 1 3 2 2 2 2 0 2 x x R x nI R dx B dB 为便于积分,用代替 x, x = Rctg , ( ) ( ) 2 2 2 2 2 2 x + R = R 1+ ctg = R csc dx R d 2 = − csc 则 = − = − 2 1 2 1 sin csc 2 csc 2 0 2 3 3 2 0 d nI R nI R d B 即: ( ) 2 1 0 cos cos 2 = − − nI B 注意:1、2 的几何意义(即取法) 讨论: 1) 轴线上的中点:此时 1 = − 2 ; 1 2 cos = −cos 而 ( ) 2 2 2 / 2 / 2 cos l R l + = ;则 ( ) 1 2 2 2 0 0 2 2 / 4 cos l R nI l B nI + = = ;若 l>>R;即无 限长的,则 nI nI B 0 0 2 2 = = ,管内磁场是均匀的。 2)若 P 点处于半无限长螺线管的一端,即 2 1 = , 2 = 0 或 1 = , 2 = / 2 , 则 B nI 0 2 1 = 3)长直螺线管内轴线上的磁感应分布如下图所 示,中部附近的磁场完全可视为均匀磁场。 运动电荷的磁场: 因电流是由自由电子定向运动形成的,可以认为电流所激发的磁场其实是由运动电 -l/2 l/2 x 0nI 0nI/2 /2 0
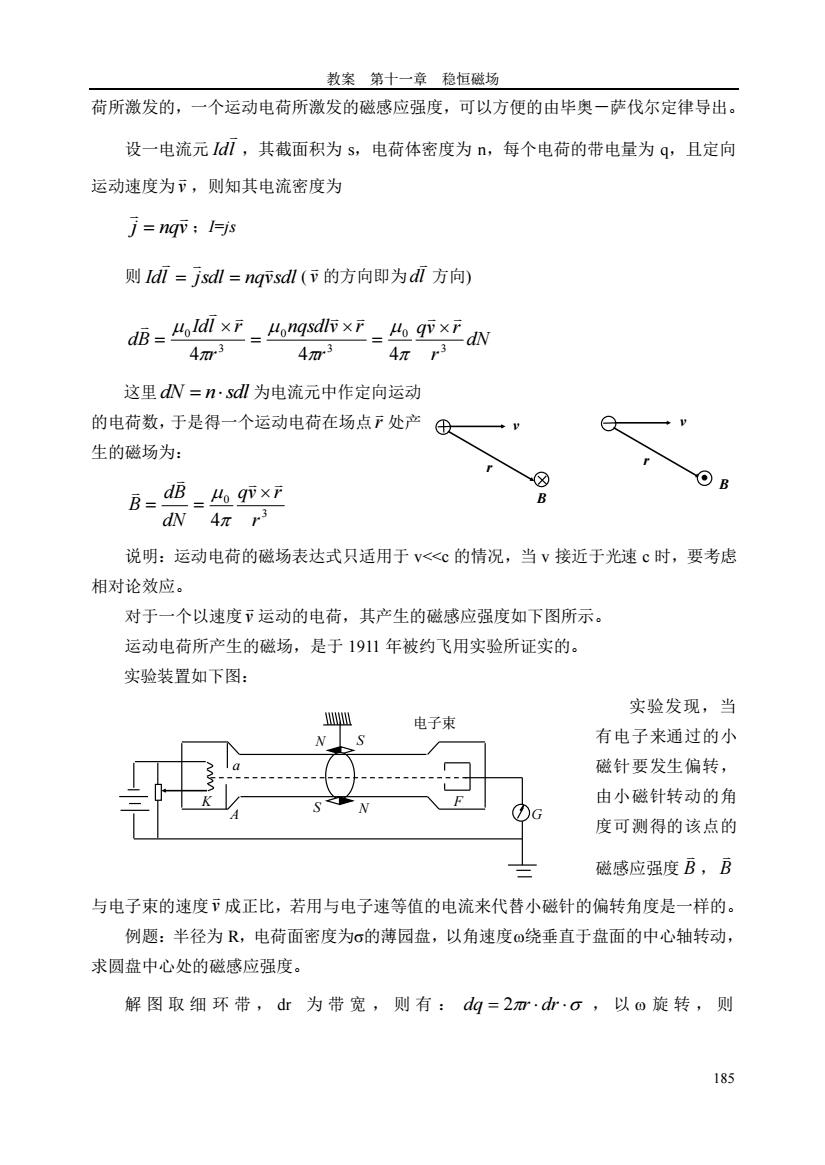
教案第十一章稳恒磁场 荷所激发的,一个运动电荷所激发的磁感应强度,可以方便的由毕奥一萨伐尔定律导出。 设一电流元d,其截面积为s,电荷体密度为,每个电荷的带电量为q,且定向 运动速度为下,则知其电流密度为 j=nqv:Ijs 则1d=jsdl=nqvsdl(下的方向即为dl方向) dB=MxF_4gxT-么rxFN 4m3 4m3 4πr3 这里dN=n~sdl为电流元中作定向运动 的电荷数,于是得一个运动电荷在场点下处产位 生的磁场为: B=B=凸9亦xF dN 4x 说明:运动电荷的磁场表达式只适用于v<c的情况,当v接近于光速c时,要考虑 相对论效应。 对于一个以速度下运动的电荷,其产生的磁感应强度如下图所示 运动电荷所产生的磁场,是于1911年被约飞用实验所证实的。 实验装置如下图: 实验发现,当 有电子来通过的小 磁针要发生偏转, 由小磁针转动的角 度可测得的该点的 磁感应强度B,B 与电子束的速度下成正比,若用与电子速等值的电流来代替小磁针的偏转角度是一样的。 例题:半径为R,电荷面密度为σ的薄园盘,以角速度0绕垂直于盘面的中心轴转动, 求圆盘中心处的磁感应强度。 解图取细环带,d为带宽,则有:dg=2m·d山o,以o旋转,则 185
教案 第十一章 稳恒磁场 185 荷所激发的,一个运动电荷所激发的磁感应强度,可以方便的由毕奥-萨伐尔定律导出。 设一电流元 Idl ,其截面积为 s,电荷体密度为 n,每个电荷的带电量为 q,且定向 运动速度为 v ,则知其电流密度为 j nqv = ;I=js 则 Idl jsdl nqvsdl = = ( v 的方向即为 dl 方向) dN r qv r r nqsdlv r r Idl r dB 3 0 3 0 3 0 4 4 4 = = = 这里 dN = nsdl 为电流元中作定向运动 的电荷数,于是得一个运动电荷在场点 r 处产 生的磁场为: 3 0 4 r qv r dN dB B = = 说明:运动电荷的磁场表达式只适用于 v<<c 的情况,当 v 接近于光速 c 时,要考虑 相对论效应。 对于一个以速度 v 运动的电荷,其产生的磁感应强度如下图所示。 运动电荷所产生的磁场,是于 1911 年被约飞用实验所证实的。 实验装置如下图: 实验发现,当 有电子来通过的小 磁针要发生偏转, 由小磁针转动的角 度可测得的该点的 磁感应强度 B , B 与电子束的速度 v 成正比,若用与电子速等值的电流来代替小磁针的偏转角度是一样的。 例题:半径为 R,电荷面密度为的薄园盘,以角速度绕垂直于盘面的中心轴转动, 求圆盘中心处的磁感应强度。 解 图 取 细 环 带 , dr 为 带 宽 , 则 有 : dq = 2r dr , 以 旋转,则 v r B v r B N S S N F G a A K 电子束

教案第十一章稳恒磁场 dl-分内=0t 由圆电流在圆心处产生的磁场公式B=得 此圆环在圆心0处所产生的磁感应强度B为: dB=Hocrardr 2r 整个圆盘在0点所产生的磁感应强度为: B=∫dB=[oart-hooR 2r 2 若圆盘带正电,则B垂直纸面向外。 若圆盘带负电,则B垂直纸面向里。 §3磁通量、磁场的高斯定理Magnetic Flux,Gaus's Theorem of Magnetic Field 1.磁感应线:(也称磁力线) 磁感应线是设想的曲线,为了用来形象的反映磁场的分布情况。磁感应线是如下规 定的。 方向:曲线上各点切线的方向就是该点的磁感应强度B的方向。 大小:磁感应线的疏密程度反映磁感应强度B的大小。 下图是几种典型的磁感应线。 无限长载流直线 长直螺线管
教案 第十一章 稳恒磁场 186 dI dq rdr = = 2 由圆电流在圆心处产生的磁场公式 R I B 2 0 = 得: 此圆环在圆心 0 处所产生的磁感应强度 B 为: r rdr dB 2 0 = 整个圆盘在 0 点所产生的磁感应强度为: 2 2 0 0 0 R r rdr B dB R = = = 若圆盘带正电,则 B 垂直纸面向外。 若圆盘带负电,则 B 垂直纸面向里。 §3 磁通量、磁场的高斯定理 Magnetic Flux,Gauss's Theorem of Magnetic Field 1.磁感应线:(也称磁力线) 磁感应线是设想的曲线,为了用来形象的反映磁场的分布情况。磁感应线是如下规 定的。 方向:曲线上各点切线的方向就是该点的磁感应强度 B 的方向。 大小:磁感应线的疏密程度反映磁感应强度 B 的大小。 下图是几种典型的磁感应线。 dr R r O 无限长载流直线 长直螺线管

教案第十一章稳恒磁场 磁感应线具有如下性质: 1两条磁感应线不会相交。这是因为磁场中某点的方向是确定的。 2载流导线周围的磁感应线为围绕电流的闭合曲线,没有起点也没有终点。 2.磁通量: 1磁感应线的密度:通过磁场中某点处垂直于B的单位面积上的磁感应线都等于该 点B的数值。 2磁通量:通过磁场中某一曲面的磁感应线数目叫作通过此曲面的磁通量。用 来表示。 即:中m=「B· 如左图,均匀磁场穿过平面s,则通过此平面的磁通应为: 中n=∫B.本=B∫d5=B5=Bscos0 nm的单位是韦伯(Wb):1Wb=1Txlm 三、磁场中的高斯定理: 由于磁力线是闭合曲线,因此,对一个闭合曲面有多少磁力线穿入,即有多少磁力 线穿出,即通过任何闭合曲面的磁通量必等于零。 fB本=0 上式即为磁场中的高斯定理,与电场中高斯定理相比较可知,它反映了磁场的无源 性,磁场是一个无源有旋场,高斯定理揭示了“磁单极”是不存在的。 说明:1931年,物理学空锹拉克预言磁单极存在,至少存在于宇宙形成的初期,几 十年来,寻找磁单极的工作一直在进行,但至今还没有令人信服的结果。 问题:若磁单极存在,我们应用的电磁理论还对吗? 麦克斯韦方程组之一∮B·5=0是否正确?需要改写吗? 例1在B-0.48T的匀强磁场中,有一长11=0.20m、宽12=0.10m的线圈,求:(1)万 与B同向,(2)万与B成30°角时的4。 解:(1)pn=[B·d5=B.5=0.48×0.20×0.10=9.6×10-3Wb (2)pm=B.5-Bs.cos30°-0.48×0.20×0.10×0.866=8.3×10-3wWb 187
教案 第十一章 稳恒磁场 187 磁感应线具有如下性质: 1 两条磁感应线不会相交。这是因为磁场中某点的方向是确定的。 2 载流导线周围的磁感应线为围绕电流的闭合曲线,没有起点也没有终点。 2.磁通量: 1 磁感应线的密度:通过磁场中某点处垂直于 B 的单位面积上的磁感应线都等于该 点 B 的数值。 2 磁通量:通过磁场中某一曲面的磁感应线数目叫作通过此曲面的磁通量。用m 来表示。 即: = s m B ds 如左图,均匀磁场穿过平面 s,则通过此平面的磁通应为: = = = = cos B ds B ds B s Bs s m m 的单位是韦伯(Wb);1Wb=1T1m2 三、磁场中的高斯定理: 由于磁力线是闭合曲线,因此,对一个闭合曲面有多少磁力线穿入,即有多少磁力 线穿出,即通过任何闭合曲面的磁通量必等于零。 = 0 B ds 上式即为磁场中的高斯定理,与电场中高斯定理相比较可知,它反映了磁场的无源 性,磁场是一个无源有旋场,高斯定理揭示了“磁单极”是不存在的。 说明:1931 年,物理学空锹拉克预言磁单极存在,至少存在于宇宙形成的初期,几 十年来,寻找磁单极的工作一直在进行,但至今还没有令人信服的结果。 问题:若磁单极存在,我们应用的电磁理论还对吗? 麦克斯韦方程组之一 = 0 B ds 是否正确?需要改写吗? 例 1 在 B=0.48T 的匀强磁场中,有一长 l1=0.20m、宽 l2=0.10m 的线圈,求:(1) n 与 B 同向,(2) n 与 B 成 30角时的m。 解:(1) 3 0.48 0.20 0.10 9.6 10− = = = = B ds B s s m Wb (2) 3 cos30 0.48 0.20 0.10 0.866 8.3 10− m = B s = Bs = = Wb n B S

教案第十一章稳恒磁场 问:何时4=0?(B⊥万时) §4安培环路定理Ampere's Circuital Law 安培环路定理是从毕奥一萨伐尔定律中严格推导而来的。 在真空中任一闭合路径上,磁感应强度B在线元d上的分量,沿该闭合路径的积分 ∮B·的值等于乘以该闭合回路所包围的各电流的代数和,即: fB.di=∑4,() iel 强调:必须是闭合回路。 说明:①若电流流向与积分回路成右旋关系时,电流取正值,反之,取负值 ②若环流为0,并不能说路径上的B值为0。 ③B是空间所有电流产生的场,其中包括那些不穿过闭合回路的电流产生的场。 (1)式说明,磁场是非保守力场。 例1长直螺线管内的B 这里谈的长直螺线管,其模型是平行电流环模型,即认为所有电流环是平行的,无 倾斜角。且是密绕的。 提问:若结?环不是平行的,而有一个倾斜角度,磁场是如何的? 选回路abcd: B.di=B.di+B.di+B.di+B.di=B-ab 即:Bab=uo abnl n为单位长度匝数 则B=4ol 可⊙可⊙可 例2螺绕环内部的B 如下图,为一螺绕环,在其内部取一半径为R的闭合回路,根据安培定律可得: 18
教案 第十一章 稳恒磁场 188 问:何时m=0?( B ⊥ n 时) §4 安培环路定理 Ampere's Circuital Law 安培环路定理是从毕奥-萨伐尔定律中严格推导而来的。 在真空中任一闭合路径上,磁感应强度 B 在线元 dl 上的分量,沿该闭合路径的积分 B dl 的值等于0 乘以该闭合回路所包围的各电流的代数和,即: = = n i i B dl I 1 0 (1) 强调:必须是闭合回路。 说明:①若电流流向与积分回路成右旋关系时,电流取正值,反之,取负值。 ②若环流为 0,并不能说路径上的 B 值为 0。 ③ B 是空间所有电流产生的场,其中包括那些不穿过闭合回路的电流产生的场。 (1)式说明,磁场是非保守力场。 例 1 长直螺线管内的 B 这里谈的长直螺线管,其模型是平行电流环模型,即认为所有电流环是平行的,无 倾斜角。且是密绕的。 提问:若结?环不是平行的,而有一个倾斜角度,磁场是如何的? 选回路 abcd: B dl B dl B dl B dl B dl B ab ab bc cd da = + + + = 即: Bab abnI = 0 n 为单位长度匝数 则 B nI = 0 例 2 螺绕环内部的 B 如下图,为一螺绕环,在其内部取一半径为 R 的闭合回路,根据安培定律可得: d a b c
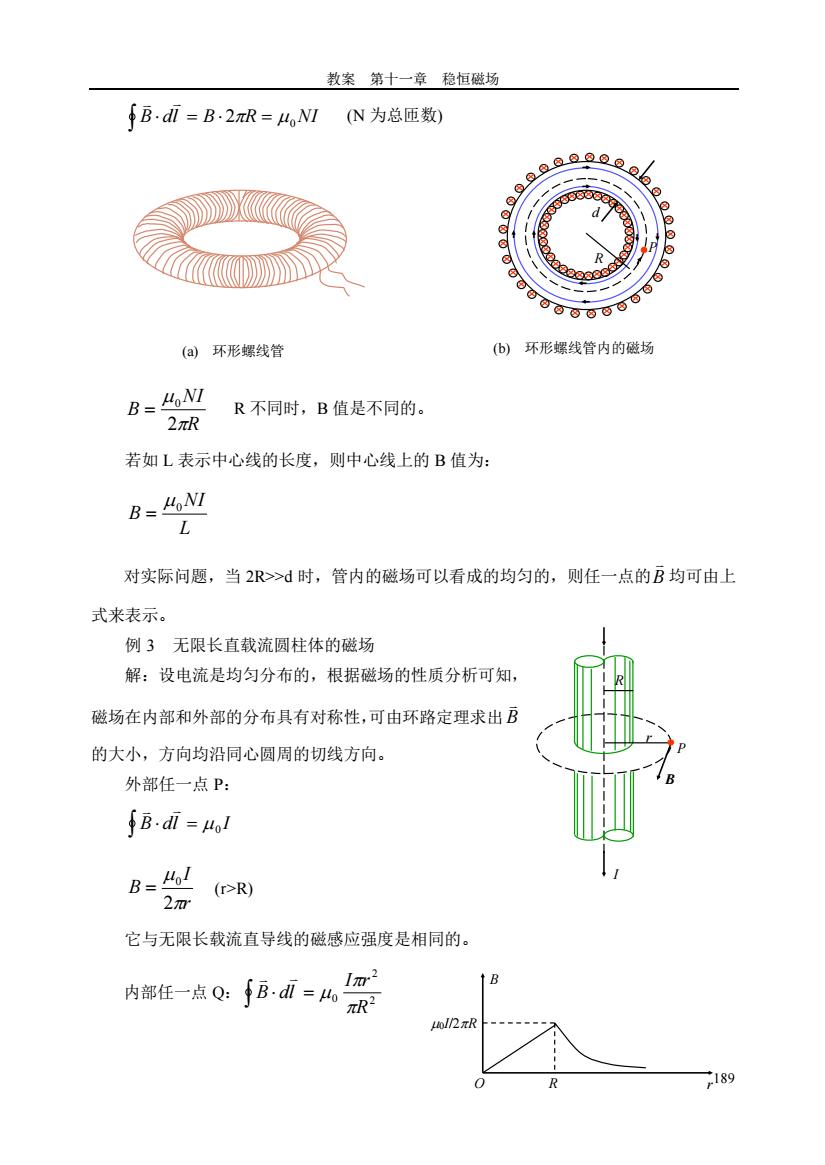
教案第十一章稳恒磁场 fB.d=B2R=4,NM(N为总匝数) (a环形螺线管 ()环形螺线管内的磁场 B=HoNI R不同时,B值是不同的。 2πR 若如L表示中心线的长度,则中心线上的B值为: B=HoNI L 对实际问题,当2>d时,管内的磁场可以看成的均匀的,则任一点的B均可由上 式来表示。 例3无限长直载流圆柱体的磁场 解:设电流是均匀分布的,根据磁场的性质分析可知 磁场在内部和外部的分布具有对称性,可由环路定理求出 的大小,方向均沿同心圆周的切线方向。 外部任一点P: fB.di=mol B=tl 2m (>R) 它与无限长载流直导线的磁感应强度是相同的。 m2 内部任一点Q:∫Bi=4R 2元 18g
教案 第十一章 稳恒磁场 189 B dl B R NI 2 = 0 = (N 为总匝数) R NI B 2 0 = R 不同时,B 值是不同的。 若如 L 表示中心线的长度,则中心线上的 B 值为: L NI B 0 = 对实际问题,当 2R>>d 时,管内的磁场可以看成的均匀的,则任一点的 B 均可由上 式来表示。 例 3 无限长直载流圆柱体的磁场 解:设电流是均匀分布的,根据磁场的性质分析可知, 磁场在内部和外部的分布具有对称性,可由环路定理求出 B 的大小,方向均沿同心圆周的切线方向。 外部任一点 P: B dl = I 0 r I B 2 0 = (r>R) 它与无限长载流直导线的磁感应强度是相同的。 内部任一点 Q: 2 2 0 R I r B dl = P R d (a) 环形螺线管 huanxingluoxianguan (b) 环形螺线管内的磁场 huanxingluoxianguan I B P R r O R r B 0I/2R