
教案第十章恒定电流 第十章恒定电流Steady Current §1电流、电流密度Electric current,.Current Density 电流:单位时间内通过截面S的电荷:即1= dt 电流密度:当电流在大块导体中流动时,导体内各处的电流分布是 不均匀的,如图所示为半球形接地电极,其中电流的分布不再是均匀的 了,为了详细地描写导体内各点电流分布情况,引入电流密度的概念 j为导体中某处的电流密度,店为在 d 该点取的面积元,刀为其法线矢量,万的 方向与该点场强E的方向相同,为通过 s的电流强度。即电流密度等于通过与该点场强方向垂直的单位截面积的电流强度。 对导体内任一截面积s有:1=∫了:本=∫jcos 电流的连续性方程:在如图所示的闭合曲面S中,从 曲面内向外流出的电荷,即通过闭合曲面向外的总电流为 d№=1=jj本 根据电荷守恒定律,它应等于曲面内单位时间内减少的 电荷-0,则有: dt f=-№ d 上式称为电流的连续性方程,即电流密度对一个闭合曲面的面积分等于该曲面内电 荷的减少率。 当曲面内的电荷不随时间变化时,行·d店=0: 即从闭合曲面上流入、流出的电流相等,曲面内无电荷积累,通过闭合曲面的电流
教案 第十章 恒定电流 176 第十章 恒定电流 Steady Current §1 电流、电流密度 Electric current, Current Density 电流:单位时间内通过截面 S 的电荷:即 dt dq I = 电流密度:当电流在大块导体中流动时,导体内各处的电流分布是 不均匀的,如图所示为半球形接地电极,其中电流的分布不再是均匀的 了,为了详细地描写导体内各点电流分布情况,引入电流密度的概念。 n dS dI j = j 为导体中某处的电流密度, ds 为在 该点取的面积元, n 为其法线矢量, n 的 方向与该点场强 E 的方向相同,dI 为通过 ds 的电流强度。即电流密度等于通过与该点场强方向垂直的单位截面积的电流强度。 对导体内任一截面积 S 有: = = s s I j ds j cosds 电流的连续性方程:在如图所示的闭合曲面 S 中,从 曲面内向外流出的电荷,即通过闭合曲面向外的总电流为 = I = j ds dt dQ 根据电荷守恒定律,它应等于曲面内单位时间内减少的 电荷 dt − dQi ;则有: dt dQ j ds i s = − 上式称为电流的连续性方程,即电流密度对一个闭合曲面的面积分等于该曲面内电 荷的减少率。 当曲面内的电荷不随时间变化时, = 0 s j ds ; 即从闭合曲面上流入、流出的电流相等,曲面内无电荷积累,通过闭合曲面的电流 I I I dS dI dS n j

教案第十章恒定电流 是恒定的,故称行·5=0为恒定电流条件。 :1=「行·5“有,1,=0一一节点的电流方程,也称基尔霍夫第一定律。 恒定条件下的电场称为恒定电场,且满足环流定理∮E·d=0, 上式在电路中可引出电压方程组,即基尔霍夫第二定律。 §2欧姆定律的微分形式Ohm Law 在导体中取一长为dl,截面积为ds的圆柱体,其轴线方向与d的方向平行,由欧姆 定律得 d山=-U R 11 U+d 而R=p业-y内电号米 ds y ds d山 则山= 6=E写成矢量形式为 8=E(2) (2)式称为欧姆定律的微分形式,它表述了大块导体中的电场和导体中的电流分布之 间逐点的细节关系地。(2)式对非稳定性情况也是适用的。 例题长为=1.00m,半径分别为rA=0.05m,rm=0.1m的圆柱形电容器,所充非理想 电介质的电阻率为p=1.00×102-m,设两相板间所加电压UrUg=1000V,求介质内各处的 场强E,电流密度δ及电阻值。 电容器中,r→r+d圆柱形薄层的电阻为R=p止= R==瑞品片 代入数据得 173
教案 第十章 恒定电流 177 是恒定的,故称 = 0 s j ds 为恒定电流条件。 ∵ I = j ds ∴有 i I i = 0 ――节点的电流方程,也称基尔霍夫第一定律。 恒定条件下的电场称为恒定电场,且满足环流定理 = 0 E dl , 上式在电路中可引出电压方程组,即基尔霍夫第二定律。 §2 欧姆定律的微分形式 Ohm Law 在导体中取一长为 dl,截面积为 ds 的圆柱体,其轴线方向与 dI 的方向平行,由欧姆 定律得 R dU dI = − 而 ds dl ds dl R 1 = = ;为电导率 则 ds R dU dI = − 上式中 = ds dI , E R dU − = ;即 = E 写成矢量形式为 E = (2) (2)式称为欧姆定律的微分形式,它表述了大块导体中的电场和导体中的电流分布之 间逐点的细节关系地。(2)式对非稳定性情况也是适用的。 例题 长为 l=1.00m,半径分别为 rA=0.05m,rB=0.1m 的圆柱形电容器,所充非理想 电介质的电阻率为=1.00109m,设两相板间所加电压 UA-UB=1000V,求介质内各处的 场强 E ,电流密度 及电阻值。 解:电容器中,r→r+dr 圆柱形薄层的电阻为 rl dr s dr dR 2 = = A B r r r r r r rl l dr R dR B A B A ln 2 2 = = = 代入数据得 dI dl dS U U+dU rB rA

教案第十章恒定电流 10L=1.10×100 1000 1=R=10x10=9,06x10A 号-914wg E=p6=100×10°×144x106L-1.44×102l.m s3电动势、基尔霍夫定律Electromotive Force,the Kirchhoff's law 1.电动势 单位正电荷绕闭合回路一周,电源(或称非静电力)所作的功称为电源的电动势。 E-fEx·dn E。为单位正电荷在电源中受的非静电力。 电动势的方向:为经电源内部从负到正。 2.基尔霍夫定律: 支点:电路中i条件或i条以上导线的会合点也称节点。 第一定律:在任一节点处,流向节点的电流之和等于流出节点的电流之和。 即/=0 一般把流向节点的电流取为负值,从节点流出的电流取为正值,当然,相反的规定 也可以。 第二定律:沿任一闭合回路的电势增量的代数和等于零。即 ΣE+ΣIR=0 计算电势增量的约定如下: (1)如果电阻中电流的方向与选定的顺序方向相同,电势增量为R反时,电势增 量为+R。 (2)若电动势方向与选定的顺序方向相同,电势增量为+E,相反时,电势增量为E。 应用基尔霍夫定律时,需注意以下几点: (1)若支路中有n个分支点,邦么只有(m-1)个分支点的方程是独立的。 178
教案 第十章 恒定电流 178 = = = 8 9 1.10 10 0.05 0.1 ln 2 3.14 1.0 1.00 10 ln 2 A B r r l R A R U I AB 6 8 9.06 10 1.10 10 1000 − = = = 6 2 6 1 1.44 10 1 2 3.14 1.0 9.06 10 2 − − − = = = = A m rl r r I S I 9 6 3 1 1 1.44 10 1 1.00 10 1.44 10− − = = = V m r r E §3 电动势、基尔霍夫定律 Electromotive Force,the Kirchhoff’s law 1.电动势 单位正电荷绕闭合回路一周,电源(或称非静电力)所作的功称为电源的电动势。 E E dl K = EK 为单位正电荷在电源中受的非静电力。 电动势的方向:为经电源内部从负到正。 2.基尔霍夫定律: 支点:电路中 i 条件或 i 条以上导线的会合点也称节点。 第一定律:在任一节点处,流向节点的电流之和等于流出节点的电流之和。 即 I = 0 一般把流向节点的电流取为负值,从节点流出的电流取为正值,当然,相反的规定 也可以。 第二定律:沿任一闭合回路的电势增量的代数和等于零。即 E +IR = 0 计算电势增量的约定如下: (1)如果电阻中电流的方向与选定的顺序方向相同,电势增量为-IR 反时,电势增 量为+IR。 (2)若电动势方向与选定的顺序方向相同,电势增量为+E,相反时,电势增量为-E。 应用基尔霍夫定律时,需注意以下几点: (1)若支路中有 n 个分支点,那么只有(n-1)个分支点的方程是独立的
教案第十章恒定电流 (2)新选定的回路不能超过少有一段电流未曾被选过。 (3)电流方向可任意假定,解得结 果若为负,说明实际电流与假定的相 反。以右图电路为例。 对B点:第一定律:+=h 对于ABCA回路:第二定律有: ΣE+IR=0 即 -E,-I1R+E2-I2R2+I3R3+E3=0 解:+山=() I:E-I,R+12R2-E2=0 Ⅱ:E2-2R2-1R,=0 RE +RE R2E+RE2 =Ri+R E等效 解得:L=RR,+R,R2+R,R:R+。2 R,+R等效 凸- 此电流的等效电路如图所示。 3.焦耳一楞次定律的微分形式 R 焦耳一楞次定律:Q=2:能量转化与守恒定律的体现。 热功率密度O:单位体积导体单位时间内所放出的热量。 对图中微元有:R=p d dQ=(d)2R·d 品图m do (ad 上式说明:导体内一点上电能与热能的转换与电场强度的平方成正比。 179
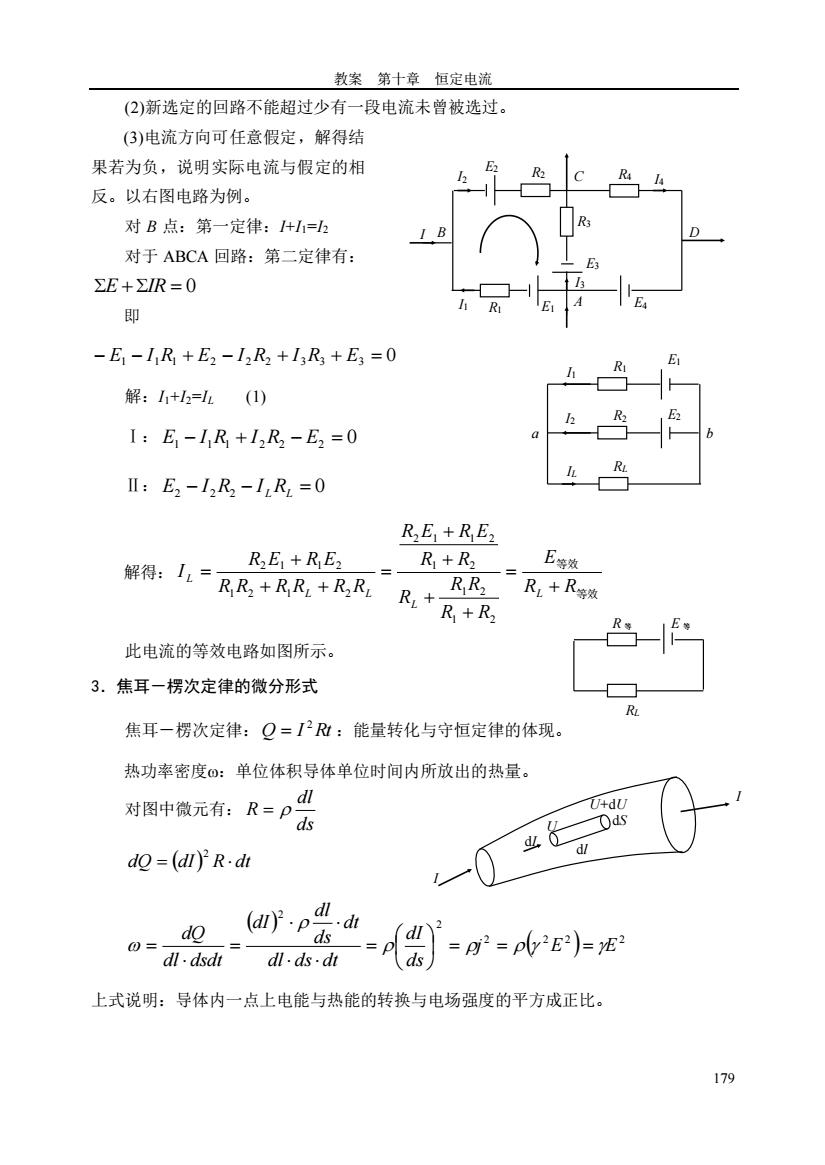
教案 第十章 恒定电流 179 (2)新选定的回路不能超过少有一段电流未曾被选过。 (3)电流方向可任意假定,解得结 果若为负,说明实际电流与假定的相 反。以右图电路为例。 对 B 点:第一定律:I+I1=I2 对于 ABCA 回路:第二定律有: E +IR = 0 即 − E1 − I 1R1 + E2 − I 2R2 + I 3R3 + E3 = 0 解:I1+I2=IL (1) Ⅰ: E1 − I 1R1 + I 2R2 − E2 = 0 Ⅱ: E2 − I 2R2 − I LRL = 0 解得: 等效 等效 R R E R R R R R R R R E R E R R R R R R R E R E I L L L L L + = + + + + = + + + = 1 2 1 2 1 2 2 1 1 2 1 2 1 2 2 1 1 2 此电流的等效电路如图所示。 3.焦耳-楞次定律的微分形式 焦耳-楞次定律: Q I Rt 2 = :能量转化与守恒定律的体现。 热功率密度:单位体积导体单位时间内所放出的热量。 对图中微元有: ds dl R = dQ = (dI) R dt 2 ( ) ( ) 2 2 2 2 2 2 j E E ds dI dl ds dt dt ds dl dI dl dsdt dQ = = = = = = 上式说明:导体内一点上电能与热能的转换与电场强度的平方成正比。 C D A I B I1 R1 E1 E4 E3 I3 I4 R2 R4 E2 I2 R3 E1 E2 R1 R2 RL I1 I2 IL a b R 等 E 等 RL I I dI dl dS U+dU U