
教案第十九章量子物理 第十九章量子物理Quantum Physics §1黑体辐射、普朗克能量子假设Blackbody Radiation,Planck Quantum Hypothesis 任何物体在任何温度下都发射电磁波,向外所辐射的能量称为辐射能,这种辐射在 量值的多少和按波长分布方面都取决于辐射体的温度,所以称为热辐射。 1.辐射出射度(辐出度) 从物体表面单位面积上所发射的各种波长的总辐射功率,称为物体的辐出度,用M (T)式M表示,单位为Wm2。 从物体表面单位面积上在单位波长间隔内所发射的功率称为单色辐出度,用M(T) 表示 4m0 实验指出,M(T)为波长入和温度T的函数。 在一定温度下时,物体的辐出度和单色辐出度的关系为 M=∑dM,=rM,(T)dn 2.吸收比、反射比 吸收比:吸收的能量和入射能量的比值,用a(、T)表示 反射比:反射的能量和入射能量的比值,用即(入、T)表示 显然:a2T)+p2T)=1 3.绝对黑体 在任何温度下对任何波长的辐射吸收比都等于1的物体,即a。=(.T)=1,显然反 射比PB=(2T)=0 在自然界,绝对黑体是不存在的,但我们可以设计绝对黑体的理想模型来进行研究, 其模型如下: 在不透明的容器壁上开有一个小孔0,当射线射入小孔 后,将在空腔内进行许多次反射,每反射一次,器壁吸收
教案 第十九章 量子物理 318 第十九章 量子物理 Quantum Physics §1 黑体辐射、普朗克能量子假设 Blackbody Radiation, Planck Quantum Hypothesis 任何物体在任何温度下都发射电磁波,向外所辐射的能量称为辐射能,这种辐射在 量值的多少和按波长分布方面都取决于辐射体的温度,所以称为热辐射。 1.辐射出射度(辐出度) 从物体表面单位面积上所发射的各种波长的总辐射功率,称为物体的辐出度,用 M (T)式 M 表示,单位为 Wm-2。 从物体表面单位面积上在单位波长间隔内所发射的功率称为单色辐出度,用 M(T) 表示 d dM M (T) = 实验指出,M(T)为波长和温度 T 的函数。 在一定温度下时,物体的辐出度和单色辐出度的关系为 M dM M (T)d 0 0 = = = 2.吸收比、反射比 吸收比:吸收的能量和入射能量的比值,用(、T)表示 反射比:反射的能量和入射能量的比值,用(、T)表示 显然: (T) + (.T) =1 3.绝对黑体 在任何温度下对任何波长的辐射吸收比都等于 1 的物体,即 B = (.T) =1 ,显然反 射比 B = (.T) = 0 在自然界,绝对黑体是不存在的,但我们可以设计绝对黑体的理想模型来进行研究, 其模型如下: 在不透明的容器壁上开有一个小孔 0,当射线射入小孔 后,将在空腔内进行许多次反射,每反射一次,器壁吸收一 O

教案第十九章量子物理 部分能量,设吸收比为a,则n次反射后,由小孔射出的能量将为1-a,若小孔的面积 远比容器的总面积小,则n很大,因而(1-a”→0,则此小孔可认为是绝对墨水体,因此, 从小孔射出的辐射,相当于从面积等于小孔面积的温度为T的绝对黑体表面射出。 4.基尔霍夫定律 任何物体的单色辐出度和单色吸收比之比,等于同一温度绝对黑体的单色辐出度。 即:M巴=M:①这就是基尔霍夫定律 d(AT) 由此可知,对某一物体,其发射本领越大,则其吸收本领也越大,若一物体不能发 射某一波长的辐射能,则它也不能吸收这一波长的辐射能。 5.绝对黑体的单色辐出度 利用如下装置可测定绝对黑体的单色辐出度。 不同波长的射线经 棱镜P后偏转角度不同, 则调节B2的方向,即可 A L B 得到不同波长的射线在 4:绝对黑体:B:平行光管:C热电偶 热电偶C上的功率,因而 可测得不同波长的功率, 即M:(T),其实验结果如下图。 根据实验结果,可得下列两条定律: 斯特劳一玻耳兹曼定律 绝对黑体的辐出度等于曲线下的面积,即 Ma(T)=[Mm(T)da 300 由实验可得: M(T)=oT4:=5.67×10'Wm2k A(tim) 称为斯特蕴恒量,这一定律也可由热力学理论导出。 维恩位移定律:由图上可见,M(T)有一最大值,其对应的波长红为,则有 Tn=b,b=2.897×103mk 根据以上两个定律,可以测量绝对黑体及其它物体的温度,此方法称为光测高温法。 黑体辐射的应用一光测高温 319
教案 第十九章 量子物理 319 部分能量,设吸收比为,则 n 次反射后,由小孔射出的能量将为(1-) n,若小孔的面积 远比容器的总面积小,则 n 很大,因而(1-) n→0,则此小孔可认为是绝对墨水体,因此, 从小孔射出的辐射,相当于从面积等于小孔面积的温度为 T 的绝对黑体表面射出。 4.基尔霍夫定律 任何物体的单色辐出度和单色吸收比之比,等于同一温度绝对黑体的单色辐出度。 即: ( ) ( . ) ( ) M T d T M T B = 这就是基尔霍夫定律 由此可知,对某一物体,其发射本领越大,则其吸收本领也越大,若一物体不能发 射某一波长的辐射能,则它也不能吸收这一波长的辐射能。 5.绝对黑体的单色辐出度 利用如下装置可测定绝对黑体的单色辐出度。 不同波长的射线经 棱镜 P 后偏转角度不同, 则调节 B2 的方向,即可 得到不同波长的射线在 热电偶 C 上的功率,因而 可测得不同波长的功率, 即 M (T ) B ,其实验结果如下图。 根据实验结果,可得下列两条定律: 斯特劳—玻耳兹曼定律: 绝对黑体的辐出度等于曲线下的面积,即 = 0 M B (T) M B (T)d 由实验可得: 4 MB (T) =T ; 8 2 4 5.67 10− − − = Wm k 称为斯特蕴恒量,这一定律也可由热力学理论导出。 维恩位移定律:由图上可见, M (T ) B 有一最大值,其对应的波长红为m,则有 T m = b ,b=2.897×10-3mk 根据以上两个定律,可以测量绝对黑体及其它物体的温度,此方法称为光测高温法。 黑体辐射的应用—光测高温 2000K 1750K 1300K 1250K ( ) (m) A L1 B1 P L2 B2 A:绝对黑体;B:平行光管;C:热电偶 C

教案第十九章量子物理 (1)消失线高温计:当调节R使灯丝F和小孔同温度时,灯丝F在背景上“消失 此时与电流对应的温度即炉温,故称为“消 失线高温计”。 高温炉小孔心 (2)根据维恩位移定律:如下图,观 察电流计最大值时热电偶位置,再测定这 位置的波长,由 T=2898x10 即可得到黑体的温度,这是因为电流 最大值代表单色辐射强度最大,太阳表面的温度就是这样测定的,在m为0.47um附近, 太阳的单色辐射强度最大,则得太阳表面温度为T= 2.898×103 0.47×10-6m =6165.967k,约为 5892.8℃。 6.黑体辐射的瑞利一金斯公式经典物理的困难 探求单色辐出度M(T)的数学表达式,对热 辐射的理论研究和实践应用都很有意义,物理学 瑞利一金斯公式 家瑞利和金斯按照经典理论得到的数学表达式 为: 实验曲线 4,(Td=2 CkT山或用入表示为 将其理论曲线与实验曲线比较,其低频部分与实验符合的很好,而高频部分根本不 与实验相符。这通常称为“紫外灾难”。 7.普朗克假设、普朗克黑体辐射公式 普朗克认为,空腔(黑体)发射电磁波时,能量不是连续的,而是一个基本单元£=h, 的整数倍,这称为普朗克量子假设,按此假设,得到普朗克黑体辐射公式为: M,(T)dy = I(T 一理论值 。··实验结果 其理论曲线与实验曲线吻合的??内,如 右图,由实验应得普朗克常数h为: h=6.63x103Js 320
教案 第十九章 量子物理 320 (1)消失线高温计:当调节 R 使灯丝 F 和小孔同温度时,灯丝 F 在背景上“消失” 此时与电流对应的温度即炉温,故称为“消 失线高温计”。 (2)根据维恩位移定律:如下图,观 察电流计最大值时热电偶位置,再测定这 一位置的波长,由 m T 3 2.898 10 − = 即可得到黑体的温度,这是因为电流 最大值代表单色辐射强度最大,太阳表面的温度就是这样测定的,在m 为 0.47m 附近, 太阳的单色辐射强度最大,则得太阳表面温度为 k m T 6165.967 0.47 10 2.898 10 6 3 = = − − ,约为 5892.8℃。 6.黑体辐射的瑞利—金斯公式 经典物理的困难 探求单色辐出度 M(T)的数学表达式,对热 辐射的理论研究和实践应用都很有意义,物理学 家瑞利和金斯按照经典理论得到的数学表达式 为: kTd C M T d 2 2 2 ( ) = 或 用 表示为 kTd C M T d 4 2 ( ) = 将其理论曲线与实验曲线比较,其低频部分与实验符合的很好,而高频部分根本不 与实验相符。这通常称为“紫外灾难”。 7.普朗克假设、普朗克黑体辐射公式 普朗克认为,空腔(黑体)发射电磁波时,能量不是连续的,而是一个基本单元 = h 的整数倍,这称为普朗克量子假设,按此假设,得到普朗克黑体辐射公式为: 1 ( ) 2 3 − = kT h e d C h M T d 其理论曲线与实验曲线吻合的??内,如 右图,由实验应得普朗克常数 h 为 : h=6.6310-34Js 高温炉 小孔 F G E R A M() 瑞利—金斯公式 实验曲线 ( ) 理论值 实验结果

教案第十九章量子物理 若用表示则为: M,(TdA=2zhc da 龙e-1 这个假设与经典物理能量连续的概念格格不入,为物理学带来新的概念和活力。 例题设有一音叉尖端的质量为0.050kg,将其频率调为y-480Hz,振幅A=1.0mm求 (1)尖端振动的量子数:(2)当量子数由n增加到+1时,振幅的变化是多少? 解:(1)尖端振动的能量为 E=m=0227J 由E=h得量子数为 4-号=715×10个 可见音叉振动的量子数是非常之大的。 (2)因为E=m2网PA,E=nhr 所以有=2元产m nh 对上式取微分有:22血 上式两边除以A2,dA→△4,dA→△n得 44=44 n 2 代入数据得△4=7.01×10m 这么微小的变化是难以觉察到的,这表明:在宏观范围内,能量量子代效应是极不 明显的,宏观物体的能量可认为是连续的。 §2光电效应、光子Photo一electronic effect,Photon 1.光电效应的实验规律: GD A 一光强大 光强小
教案 第十九章 量子物理 321 若用表示则为: 1 2 ( ) 5 2 − = kT hc e hC d M T d 这个假设与经典物理能量连续的概念格格不入,为物理学带来新的概念和活力。 例题 设有一音叉尖端的质量为 0.050kg,将其频率调为=480Hz,振幅 A=1.0mm 求 (1)尖端振动的量子数;(2)当量子数由 n 增加到 n+1 时,振幅的变化是多少? 解:(1)尖端振动的能量为 E m A m(2 ) A 0227J 2 1 2 1 2 2 2 2 = = = 由 E=nh得量子数为 29 = = 7.1310 h E n 个 可见音叉振动的量子数是非常之大的。 (2)因为 2 2 (2 ) 2 1 E = m A ,E=nh 所以有 m nh A 2 2 2 = 对上式取微分有: dn m nh AdA 2 2 2 = 上式两边除以 A2, dA → A , dA → n 得 2 A n n A = 代入数据得 A m 34 7.01 10− = 这么微小的变化是难以觉察到的,这表明:在宏观范围内,能量量子代效应是极不 明显的,宏观物体的能量可认为是连续的。 §2 光电效应、光子 Photo-electronic effect, Photon 1. 光电效应的实验规律: V G K A GD 光 光强大 光强小 I -U0 O U IH2 IH1

教案第十九章量子物理 从光电效应实验中,可以归纳出如下规律: 1当以一定频率和强度的光照射K极时,光电流随加速电压的改变而变,如图2 所示,此曲线为光电效应的伏安特性曲线,H称为饱和和光电流,U0称为遏止电压,若 所用的光频率相同而光强不同,则其遏止电势差不变,光强越大,饱和电流日也越大。 给出)m2=e, 2用不同频率的光照射K极时,频率越高, 遏止电势差越大,而且只有当入射光的频率大于 某一频率时,才有光电流,当入射光的频率小于 0时,则无论入射光的强度多强,电路中都无光 电流,0叫作截止频率,:也称红限,如左图所示。 3无论入射光的强度如何,只需其频率大于 截止频率,则只要光照射到金属表面时,立刻就有光电子逸出,这就是光电效应的“瞬 时性”。 2.爱因斯坦的光电效应量子理论: 光是由大量光子构成的,对于频率为的光束,光子的能量为:£=hy,据此提出光 电效应爱因斯坦方程: hi-m+o (1) ω为电子从金属表面逸出时需要作的功,为逸出功。 以方程(1)可成功的解释前面三条实验规律: 光子的静止质量:m0=0 能量:E=h 运动能量:m名 动量:P=g 3.光电效应的应用 (1)光控继电器:应用于自动控制,如下图 (2)光电倍增管:测量微弱的光 例1用=4000A的光照射铯时,求光电子的初速度,已知铯的逸出功为:=hy
教案 第十九章 量子物理 322 从光电效应实验中,可以归纳出如下规律: 1 当以一定频率和强度的光照射 K 极时,光电流随加速电压的改变而变,如图 2 所示,此曲线为光电效应的伏安特性曲线,IH 称为饱和和光电流,U0 称为遏止电压,若 所用的光频率相同而光强不同,则其遏止电势差不变,光强越大,饱和电流 IH 也越大。 给出 0 2 2 1 mv = ev 2 用不同频率的光照射 K 极时,频率越高, 遏止电势差越大,而且只有当入射光的频率大于 某一频率时,才有光电流,当入射光的频率小于 0 时,则无论入射光的强度多强,电路中都无光 电流,0 叫作截止频率,;也称红限,如左图所示。 3 无论入射光的强度如何,只需其频率大于 截止频率,则只要光照射到金属表面时,立刻就有光电子逸出,这就是光电效应的“瞬 时性”。 2.爱因斯坦的光电效应量子理论: 光是由大量光子构成的,对于频率为的光束,光子的能量为: = h ,据此提出光 电效应爱因斯坦方程: = + 2 2 1 h mv (1) 为电子从金属表面逸出时需要作的功,为逸出功。 以方程(1)可成功的解释前面三条实验规律: 光子的静止质量:m0=0 能量:E=h 运动能量: 2 C h m = 动量: C h P = 3.光电效应的应用 (1)光控继电器:应用于自动控制,如下图 (2)光电倍增管:测量微弱的光 例 1 用=4000Å 的光照射铯时,求光电子的初速度,已知铯的逸出功为: 0 = h , U0 O
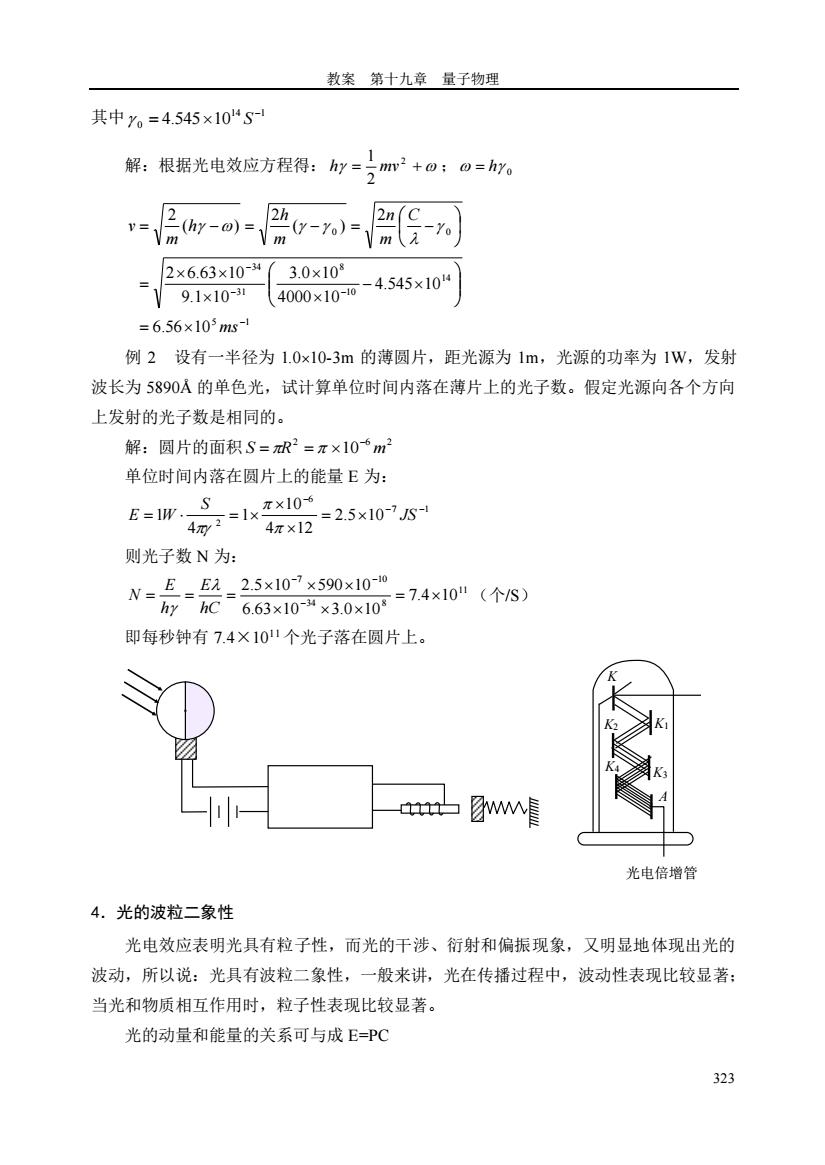
教案第十九章量子物理 其中。=4.545×10“S 解:根据光电效应方程得:r=m2+o:o=hr。 2x6.63×10- 3.0×10 =9.1x100 4000×10-H0 -4.545x104 =6.56×103ms 例2设有一半径为1.0x10-3m的薄圆片,距光源为1m,光源的功率为1W,发射 波长为5890A的单色光,试计算单位时间内落在薄片上的光子数。假定光源向各个方向 上发射的光子数是相同的: 解:圆片的面积S=R2=π×10‘m 单位时间内落在圆片上的能量E为: π×106 =2.5×10-7JS- 则光子数N为: -号-是-名0o-140个 即每秒钟有7.4×101个光子落在圆片上。 m白☑M虐 光电倍增管 4.光的波粒二象性 光电效应表明光具有粒子性,而光的干涉、衍射和偏振现象,又明显地体现出光的 波动,所以说:光具有波粒二象性,一般来讲,光在传播过程中,波动性表现比较显著: 当光和物质相互作用时,粒子性表现比较显著。 光的动量和能量的关系可与成E=PC 323
教案 第十九章 量子物理 323 其中 14 1 0 4.545 10 − = S 解:根据光电效应方程得: = + 2 2 1 h mv ; 0 = h 5 1 14 10 8 31 34 0 0 6.56 10 4.545 10 4000 10 3.0 10 9.1 10 2 6.63 10 2 ( ) 2 ( ) 2 − − − − = − = = − = − = − ms C m n m h h m v 例 2 设有一半径为 1.010-3m 的薄圆片,距光源为 1m,光源的功率为 1W,发射 波长为 5890Å 的单色光,试计算单位时间内落在薄片上的光子数。假定光源向各个方向 上发射的光子数是相同的。 解:圆片的面积 2 6 2 S R 10 m − = = 单位时间内落在圆片上的能量 E 为: 7 1 6 2 2.5 10 4 12 10 1 4 1 − − − = = = JS S E W 则光子数 N 为: 11 34 8 7 10 7.4 10 6.63 10 3.0 10 2.5 10 590 10 = = = = − − − hC E h E N (个/S) 即每秒钟有 7.4×1011 个光子落在圆片上。 4.光的波粒二象性 光电效应表明光具有粒子性,而光的干涉、衍射和偏振现象,又明显地体现出光的 波动,所以说:光具有波粒二象性,一般来讲,光在传播过程中,波动性表现比较显著; 当光和物质相互作用时,粒子性表现比较显著。 光的动量和能量的关系可与成 E=PC K K2 K4 K1 K3 A 光电倍增管

教案第十九章量子物理 P名9 即:H=:P=号 上式可以看出,光的粒子性描述量E和P通过普朗克常数h和描述光的波动性的量) 和y联系在起,故通常把h称为作用量子。 §3康普顿效应Compton Effect 1922~23年间,康普顿(AH.Compton)研究院x射线经金属、石墨等物质的散射 现象,实验结果指出:散射分式中有与入射波长相同的波线,也有大于入射波波长的射 线,这种改变波长的散射称为康普顿效应,波长的改变△随散射角而异,当散射角增加 时,波长的改变也随之增加。 入射线 60 090 X射线源 射谱仪 实验示意图 实验结果图 按经典理论,散射波的频率与入射光的频率相同,解释不了康普顿效庆。 如果应用光子概念,假设光子和实物粒子一样,能与电子等粒子发生弹性碰撞,即 可解释康普顿效应,因为:碰撞时,光子的能量?给电子,故散射波的波长变长。 康普顿效应不仅有力的证实了光子假设的正确性,而且证实了在微观粒子的相互作 用过程中,也严格的遵守能量守恒和动量守恒。 康普顿效应的推导: 如图:碰撞时动量、能量守恒: (hwle)n hyo+moC2 =hy +mc2 (1) h
教案 第十九章 量子物理 324 h C h C E P = = = 即: H = h ; h P = 上式可以看出,光的粒子性描述量 E 和 P 通过普朗克常数 h 和描述光的波动性的量 和联系在起,故通常把 h 称为作用量子。 §3 康普顿效应 Compton Effect 1922~23 年间,康普顿(A.H.Compton)研究院 x 射线经金属、石墨等物质的散射 现象,实验结果指出:散射分式中有与入射波长相同的波线,也有大于入射波波长的射 线,这种改变波长的散射称为康普顿效应,波长的改变随散射角而异,当散射角增加 时,波长的改变也随之增加。 按经典理论,散射波的频率与入射光的频率相同,解释不了康普顿效庆。 如果应用光子概念,假设光子和实物粒子一样,能与电子等粒子发生弹性碰撞,即 可解释康普顿效应,因为:碰撞时,光子的能量?给电子,故散射波的波长变长。 康普顿效应不仅有力的证实了光子假设的正确性,而且证实了在微观粒子的相互作 用过程中,也严格的遵守能量守恒和动量守恒。 康普顿效应的推导: 如图:碰撞时动量、能量守恒: 2 2 h 0 + m0C = h + mC (1) 光阑 X 射线源 0 散射物质 射谱仪 实验示意图 0 入射线 =0 =45 =90 =135 实验结果图 (h0/c)n (h0/c)n0 mv x

教案第十九章量子物理 处元,-g万+m 动量守恒方程可写为:(余弦定理): om-2-竖名w 即:m2v2C2=y6+y2-2h2 Yoycos6 (2) 将(1)式平方减去(2)式得: mcca-co)mc 化为:C,-2.h0-c0s Yor moc 操后写房-大染n号 (3) 由(3)式可以看出,波长改变与散射物质无关,仅决定于散射方向,当散射角增 大时,0也将随之增加,并且-.0的理论值也能与实验结果相结合。 (3)式中h叫康普顿波长,是一个常数: 6.63×10-4 即:C2n1i03x10=24x10m=0243A 由(3)式可以看出,波长的改变量与入射光的波长无关,对于波长较长的可见光, 波长的政支量A与入射光的波长相比小得多。例如:10m的微流,兰-243×10。 因此观察不到康普顿效应,这时量子结果与经典结果是一致的。而对=1A 兰-20:这时才能发察到康额效应。这种情况下,经真结果就失效了。 例题:设波长入,=1.00×10~°m的x射线与自由电子弹性碰撞,散射角0=90°,问 (1)散射波长的改变是A为多少? (2)反冲电子得到多少动能? (3)在碰撞中,光子能量损失了多少? 解:)根据公式有:△2=h (-cos0) 6.63×10-34 甲A以=21n0×3000-ecos909)=243x10-9m 名
教案 第十九章 量子物理 325 n mv C h n C h = + 0 0 动量守恒方程可写为:(余弦定理): ( ) 2 cos 0 2 2 2 0 C h C h C h C h mv − + = 即: 2 0 cos 2 2 2 2 0 2 2 2 2 m v C = h + h − h (2) 将(1)式平方减去(2)式得: 1 2 (1 cos ) 2 ( ) 0 2 0 0 2 4 2 2 0 2 2 4 = − − + − − m C h m C h C v m C 化为: (1 cos ) ( ) 0 0 0 = − − m C C h 最后写为: 2 sin 2 2 0 0 m C h − = (3) 由(3)式可以看出,波长改变与散射物质无关,仅决定于散射方向,当散射角增 大时,-0 也将随之增加,并且-0 的理论值也能与实验结果相结合。 (3)式中 m C h 0 叫康普顿波长,是一个常数: 即: 2.43 10 0.0243 9.11 10 3 10 6.63 10 12 31 4 34 0 = = = − − − m m C h Å; 由(3)式可以看出,波长的改变量与入射光的波长无关,对于波长较长的可见光, 波长的改变量与入射光的波长相比小得多。例如:=10cm 的微波, 11 2.43 10 − = , 因此观察不 到康普 顿效应, 这时量子 结果与 经典结果 是一致 的。而对 =1Å, 2 2.43 10 − = ;这时才能观察到康普顿效应,这种情况下,经典结果就失效了。 例题:设波长 10 0 1.00 10− = m 的 x 射线与自由电子弹性碰撞,散射角=90,问 (1)散射波长的改变是为多少? (2)反冲电子得到多少动能? (3)在碰撞中,光子能量损失了多少? 解:(1)根据公式有: (1 cos ) 0 = − m C h 即 m 12 31 8 34 (1 cos90 ) 2.43 10 9.11 10 3.0 0 6.63 10 − − − − = =

教案第十九章量子物理 (2)根据能量守恒有:mC2-m,C2=hy。-h似 即: E=。-=ChC 入。1 1 =d+a hC△M =+△网 =295eV (3)因为能量守恒,光子损失的能量等于反冲电子获得的动能 s4氢原子的玻耳理论Bohr Hydrogence-一atomic Theory 1.原子光谱的实验规律: 1讲述原子光谱的作用和用途 H原子光谱: 巴乐末(J.Balmer)经验公式:由实验数据总结得出: =8657A:m3.45 1 R=音=1.09676×P'm称为里德伯常数(Rydbeng) 2里兹合并原理(W.Ritz) 碱金属:氵=Tk)-Tm) Tk)、Tn)称为光谱项 R 7k+aTn+所 iim 1 H原子的帕邢系(F.Paschen): 7一仔习:这他是由实验意结出的公式
教案 第十九章 量子物理 326 (2)根据能量守恒有: mC − m C = h − h 0 2 0 2 即: eV hC hC hC hC E h h k 295 ( ) 1 1 0 0 0 0 0 0 = + = + = + = − = − (3)因为能量守恒,光子损失的能量等于反冲电子获得的动能。 §4 氢原子的玻耳理论 Bohr Hydrogence-atomic Theory 1.原子光谱的实验规律: 1 讲述原子光谱的作用和用途 H 原子光谱: 巴乐末(JJ.Balmer)经验公式:由实验数据总结得出: 4 2 2 − = n n B ;B=3645.7Å;n=3,4,5…… = − = − − = = 2 2 2 2 2 2 1 2 1 1 2 4 4 1 n RC B n C C Bn C n 或: = = − 2 2 1 2 ~ 1 1 n R 7 1 1.096776 1 4 − − = = m B R 称为里德伯常数(Rydbeng) 2 里兹合并原理(W.Ritz) 碱金属: ( ) ( ) ~ = T k −T n T(k)、T(n)称为光谱项 2 ( +) = k R Tk ; 2 ( + ) = n R Tn 即: + − + = 2 2 ( ) 1 ( ) ~ 1 k n R H 原子的帕邢系(F.Paschen): = − 2 2 1 3 ~ 1 n R ;这也是由实验总结出的公式

教案第十九章量子物理 根据大量的实验数据,总结出H原子的光谱有如下规律: (1)波数由两个谱项的差值决定。 (2)前项决定以后,后项取不同值,可给出同一线系中不同谱线的波数。 (3)改变前项的值,可给出不同的线系。 对于这些现象,当时只停留在实验阶段,不能给出满意的理论解释。 2.卢瑟福的原子核模型 原子的核型结构 19Il年,E.Ruthenford在x粒子散射实验的基础上,提出了原子的核型结构的理论, 如下图: 缺点:①按经典理论,由于在核外做变速圆周运动时 应以辐射电磁波的形式向外辐射能量,与圆周运动的频率 核外由子 相对应,电磁波也是这一频率,这样,能量将逐渐减小 从而频率改变,光谱应是连续的,而实验并非如此:②电 子半径逐渐减少,最后将落后在原子核上,这也与实验不 符。 这是经典理论所面临的困难,怎样解决这个困难是比较重要的课题,1913年,玻尔 提出大胆的假设。 3.氢原子的玻耳理论 1玻尔理论的基本假设:(当时是针对H原子提出的) ①能量是量子化的,处于稳定态的原子的电子,绕核作圆周运动,但不辐射能量, ②轨道是量子化的,其矩L=名:=1.2n为量子致 ③电子跃迁时,发射或吸收能量为:hy=E。-E, 2H原子轨道半径和能量的计算 根聚牛锁定排有号 2 (1) 又由假设(2):L=my=nh (2) e1,2,3
教案 第十九章 量子物理 327 根据大量的实验数据,总结出 H 原子的光谱有如下规律: (1)波数由两个谱项的差值决定。 (2)前项决定以后,后项取不同值,可给出同一线系中不同谱线的波数。 (3)改变前项的值,可给出不同的线系。 对于这些现象,当时只停留在实验阶段,不能给出满意的理论解释。 2.卢瑟福的原子核模型 原子的核型结构 1911 年,E.Ruthenford 在 x 粒子散射实验的基础上,提出了原子的核型结构的理论, 如下图: 缺点:①按经典理论,由于在核外做变速圆周运动时, 应以辐射电磁波的形式向外辐射能量,与圆周运动的频率 相对应,电磁波也是这一频率,这样,能量将逐渐减小, 从而频率改变,光谱应是连续的,而实验并非如此;②电 子半径逐渐减少,最后将落后在原子核上,这也与实验不 符。 这是经典理论所面临的困难,怎样解决这个困难是比较重要的课题,1913 年,玻尔 提出大胆的假设。 3.氢原子的玻耳理论 1 玻尔理论的基本假设:(当时是针对 H 原子提出的) ①能量是量子化的,处于稳定态的原子的电子,绕核作圆周运动,但不辐射能量。 ②轨道是量子化的,其量矩 n h L = n = 2 ;n=1,2……;n 为量子数 ③电子跃迁时,发射或吸收能量为: h = En − Ek 2 H 原子轨道半径和能量的计算: 根据牛顿定律有: 2 2 0 2 4 v m e = (1) 又由假设(2): L = mv = n (2) 由(1)、(2)两式解得: 2 2 2 2 0 2 2 4 0 n me h n me n = = (3) n=1,2,3…… 原子核 核外电子