
教案第十七章波动光学 第十七章波动光学Optics 光学是物理学的一个重要组成部分。17世纪和18世纪是光学发展史上的一个重要时 期,在这段时间内,科学家们不仅开始从实验上对光学进行研究,而且也着手进行已有 光学知识的系统化、理论化。这一时期,对光本性的认识存在着争论。牛顿支持光的微 粒说,用微粒说不仅可以说明光的直线传播,而且可以说明光的反射和折射,只不过在 说明折射时,认为光在水中的速度要大于空气中的速度:惠更斯提倡波动说,利用波动 说也能说明反射和折射现象,而且还解释了方解石的双折射现象,但认为光在水中的速 度要小于在空气中的速度。此外在说明光的直线传播时,波动说也遇到了困难。 19世纪系统地用光的波动说和干涉原理研究了光的干涉、衍射和偏振,认识到了光 的横波特性,并且用波动说满意地解释了光的直线传播现象:实验上测出了光在水中的 速度比空气中的小,波动说取得了决定性的胜利,而在理论上找到了光和电磁波之间的 联系,莫定了光的电磁理论的基础。 到了19世纪末和20世纪初期,人们通过对黑体辐射、光电效应和康普顿效应的可 究,无可怀疑地证实了光的量子性,形成了一种具有崭新内涵的微粒学说。此时人们对 光的本质认识又前进了一大步,承认光具有波粒二象性。 20世纪60年代激光的发现,使光学的发展又获得了新的活力,非线性光学、傅里叶 光学等现代光学分支逐渐形成,带动了物理学及其相关学科的不断发展。 基本要求 光的干涉部分: 1理解光的相干条件及获得相干光的基本原理和方法: 2作为杨氏双缝干涉实验的基本装置和实验规律及干涉条纹位置的计算: 3确切理解光程的概念,掌握光程和光程差的计算方法,熟悉光程差和相位差之间 的关系,理解什么情况下有半波损失,什么情况下无半波损失: 4掌握薄膜等厚干涉的规律及干涉位置的计算,理解等倾干涉条件产生的原理,掌 握薄膜干涉原理在实际中的应用: 5了解迈克尔孙干涉仪的工作原理和应用。 光的衍射部分: 1理解惠更斯一菲捏耳原理及其在光的衍射现象中的应用: 2了解菲涅耳衍射及夫琅和费衍射的区别,理解夫琅和费衍射的规律,掌握半波带 法在分析夫琅和费衍射中的应用: 3理解瑞利判据,能定性分析衍射对光学仪器分辨能力的影响: 4理解光栅衍射条纹的成因和特点,掌握光栅方程和暗纹形成条件及它们的应用: 5理解X射线衍射的原理,了解布喇格公式在品格常数和X射线波长测量方面的应 用。 266
教案 第十七章 波动光学 266 第十七章 波动光学 Optics 光学是物理学的一个重要组成部分。17 世纪和 18 世纪是光学发展史上的一个重要时 期,在这段时间内,科学家们不仅开始从实验上对光学进行研究,而且也着手进行已有 光学知识的系统化、理论化。这一时期,对光本性的认识存在着争论。牛顿支持光的微 粒说,用微粒说不仅可以说明光的直线传播,而且可以说明光的反射和折射,只不过在 说明折射时,认为光在水中的速度要大于空气中的速度;惠更斯提倡波动说,利用波动 说也能说明反射和折射现象,而且还解释了方解石的双折射现象,但认为光在水中的速 度要小于在空气中的速度。此外在说明光的直线传播时,波动说也遇到了困难。 19 世纪系统地用光的波动说和干涉原理研究了光的干涉、衍射和偏振,认识到了光 的横波特性,并且用波动说满意地解释了光的直线传播现象;实验上测出了光在水中的 速度比空气中的小,波动说取得了决定性的胜利,而在理论上找到了光和电磁波之间的 联系,奠定了光的电磁理论的基础。 到了 19 世纪末和 20 世纪初期,人们通过对黑体辐射、光电效应和康普顿效应的研 究,无可怀疑地证实了光的量子性,形成了一种具有崭新内涵的微粒学说。此时人们对 光的本质认识又前进了一大步,承认光具有波粒二象性。 20 世纪 60 年代激光的发现,使光学的发展又获得了新的活力,非线性光学、傅里叶 光学等现代光学分支逐渐形成,带动了物理学及其相关学科的不断发展。 一 基本要求 光的干涉部分: 1 理解光的相干条件及获得相干光的基本原理和方法; 2 作为杨氏双缝干涉实验的基本装置和实验规律及干涉条纹位置的计算; 3 确切理解光程的概念,掌握光程和光程差的计算方法,熟悉光程差和相位差之间 的关系,理解什么情况下有半波损失,什么情况下无半波损失; 4 掌握薄膜等厚干涉的规律及干涉位置的计算,理解等倾干涉条件产生的原理,掌 握薄膜干涉原理在实际中的应用; 5 了解迈克尔孙干涉仪的工作原理和应用。 光的衍射部分: 1 理解惠更斯-菲涅耳原理及其在光的衍射现象中的应用; 2 了解菲涅耳衍射及夫琅和费衍射的区别,理解夫琅和费衍射的规律,掌握半波带 法在分析夫琅和费衍射中的应用; 3 理解瑞利判据,能定性分析衍射对光学仪器分辨能力的影响; 4 理解光栅衍射条纹的成因和特点,掌握光栅方程和暗纹形成条件及它们的应用; 5 理解 X 射线衍射的原理,了解布喇格公式在晶格常数和 X 射线波长测量方面的应 用

教案第十七章波动光学 光的偏振部分: 1理解自然光和线偏振光概念,掌握用偏振片起偏和检偏的方法: 2理解产生偏振光的几种方法:了解反射光、折射光的偏振特性,掌握布儒斯特定 律,掌握马吕斯定律: 3理解光轴和主平面的概念:掌握单轴品体中o光和e光的传播特点: 4了解局振光干涉的原理和应用。 二基本内容 光的干涉部分: 1光的相关性 )相干光:满足相干条件(频率相同、相位差恒定、振动方向不相互垂直)的两束光。 2)光程:光在折射率为n的介质中传播了1距离,则其相应的光程为L=l。 3)半波损失:光从光疏介质(折射率较小)射向光密介质(折射率较大),在界面上反 射时反射光相位突变元,相当于损失了2的光程。(1为该光在真空中的波长) 4)相干长度:即一个波列的长度。原子发光前后两列波并不相干,当一列波分为二子波 列经不同途径后相遇能发生干涉,若不同途径的光程差超过了波列长度,则相遇的将 不是“李生”子波,即两列子波不相干,所以把波列长度称为相干长度 5)干涉相长与相消:两束相干光在相遇点的光程差(包括半波损失)是的整数倍时, 该点为明条纹中心,称干涉相长:是2的奇数倍时,该点为暗条纹中心,称干涉相 消。 2分波面干涉 同一波阵面上两点作为次级光源,则频率、相位、振动方向都相同,二相干光源可 产生干涉。 )杨氏双缝干涉实验:典型的分波阵面干涉例子,干涉条纹为等间距明暗相间的条纹, 间距 其中:D为双缝到观察屏的间距:d为双缝间距:为波长。 2)劳埃德实验:条纹间距与杨氏实验相同。但由于反射光受镜面长度的限制及半波损失, 所以只在部分区域有干涉条纹,且与相应的杨氏双缝实验比较,明、暗条纹中心位置交 换。 3分振幅干涉 光在薄膜上表面由于反射与透射而分开为二列波。透射光在下表面反射后又与上表 267
教案 第十七章 波动光学 267 光的偏振部分: 1 理解自然光和线偏振光概念,掌握用偏振片起偏和检偏的方法; 2 理解产生偏振光的几种方法;了解反射光、折射光的偏振特性,掌握布儒斯特定 律,掌握马吕斯定律; 3 理解光轴和主平面的概念;掌握单轴晶体中 o 光和 e 光的传播特点; 4 了解偏振光干涉的原理和应用。 二 基本内容 光的干涉部分: 1 光的相关性 1) 相干光:满足相干条件(频率相同、相位差恒定、振动方向不相互垂直)的两束光。 2) 光程:光在折射率为 n 的介质中传播了 l 距离,则其相应的光程为 L=nl。 3) 半波损失:光从光疏介质(折射率较小)射向光密介质(折射率较大),在界面上反 射时反射光相位突变,相当于损失了/2 的光程。(为该光在真空中的波长) 4) 相干长度:即一个波列的长度。原子发光前后两列波并不相干,当一列波分为二子波 列经不同途径后相遇能发生干涉,若不同途径的光程差超过了波列长度,则相遇的将 不是“孪生”子波,即两列子波不相干,所以把波列长度称为相干长度。 5) 干涉相长与相消:两束相干光在相遇点的光程差(包括半波损失)是的整数倍时, 该点为明条纹中心,称干涉相长;是/2 的奇数倍时,该点为暗条纹中心,称干涉相 消。 2 分波面干涉 同一波阵面上两点作为次级光源,则频率、相位、振动方向都相同,二相干光源可 产生干涉。 1) 杨氏双缝干涉实验:典型的分波阵面干涉例子,干涉条纹为等间距明暗相间的条纹, 间距 d D x = 其中:D 为双缝到观察屏的间距;d 为双缝间距;为波长。 2) 劳埃德实验:条纹间距与杨氏实验相同。但由于反射光受镜面长度的限制及半波损失, 所以只在部分区域有干涉条纹,且与相应的杨氏双缝实验比较,明、暗条纹中心位置交 换。 3 分振幅干涉 光在薄膜上表面由于反射与透射而分开为二列波。透射光在下表面反射后又与上表

教案第十七章波动光学 面的反射光相遇而发生干涉,此种干涉称为薄膜干涉。 )厚干涉条纹:光以确定的入射角入射(通常垂直入射),薄膜厚度相等处干涉情况 一样。空气中的劈尖,干涉条纹是等间距直条纹:凸透镜与平板玻璃形成的空气楔,干 涉条纹是牛顿环。 2)等倾干涉条纹:薄膜厚度均匀,以相同倾角入射的光,干涉情况一样。当会聚透镜的 主光轴与反射光一致,在透镜焦平面上观察到干涉条纹是内疏外密的同心圆环。 光的衍射部分: 1惠更斯一菲涅耳原理:波阵面上各点都可看作相干的次波波源,次波波源发出的次波 在空间各点相遇时,其强度分布是相干叠加的结果: 2单缝夫琅和费衍射:波长为的单色光垂直入射时,衍射暗纹中心的位置为 asin0=±k2,(k=1,2,3) 其中:a为单缝宽度,伪衍射角。 第k级明纹离焦点距离为:x=kD以 两个1级暗条纹的所夹空间称为中央明纹,中央明纹的中心中焦点处,其宽度是其他各 级明纹宽度的2倍,为 4水,-22=2 单缝夫琅和费衍射的光强分布为 1=1o 3瑞利判据:如果一个像点的爱里斑的中心刚好与另一像点衍射图样的第一级暗纹相重 合,就认为这两个物点恰好能为这一光学仪器分辨。 最小分辨角:成=122合 其中:D为圆孔直径,为入射光的波长。 4光栅衍射 光栅方程:(a+b)sim日=±k2,(k=0l,2,) 其中:a+b为光栅常数,为衍射角。 由于单缝衍射的调制作用,当光栅常数d与通光缝宽a为整数比,即 268
教案 第十七章 波动光学 268 面的反射光相遇而发生干涉,此种干涉称为薄膜干涉。 1) 厚干涉条纹:光以确定的入射角入射(通常垂直入射),薄膜厚度相等处干涉情况 一样。空气中的劈尖,干涉条纹是等间距直条纹;凸透镜与平板玻璃形成的空气楔,干 涉条纹是牛顿环。 2) 等倾干涉条纹:薄膜厚度均匀,以相同倾角入射的光,干涉情况一样。当会聚透镜的 主光轴与反射光一致,在透镜焦平面上观察到干涉条纹是内疏外密的同心圆环。 光的衍射部分: 1 惠更斯-菲涅耳原理:波阵面上各点都可看作相干的次波波源,次波波源发出的次波 在空间各点相遇时,其强度分布是相干叠加的结果; 2 单缝夫琅和费衍射:波长为的单色光垂直入射时,衍射暗纹中心的位置为 a sin = k, (k =1,2,3, ) 其中:a 为单缝宽度,为衍射角。 第 k 级明纹离焦点距离为: a D x k k = 两个 1 级暗条纹的所夹空间称为中央明纹,中央明纹的中心中焦点处,其宽度是其他各 级明纹宽度的 2 倍,为 k x a f x 2 2 0 = = 单缝夫琅和费衍射的光强分布为 2 2 0 sin sin sin = a a I I 3 瑞利判据:如果一个像点的爱里斑的中心刚好与另一像点衍射图样的第一级暗纹相重 合,就认为这两个物点恰好能为这一光学仪器分辨。 最小分辨角: D =1.22 其中:D 为圆孔直径,为入射光的波长。 4 光栅衍射 光栅方程: (a + b)sin = k, (k = 0,1,2, ) 其中:a+b 为光栅常数,为衍射角。 由于单缝衍射的调制作用,当光栅常数 d 与通光缝宽 a 为整数比,即

教案第十七章波动光学 d m a-m 时,±m,±2m,士3m,…级明纹将不出现,这就是缺级现象。 暗纹条件:N(a+b)sin0=±ma,(m=l,2,3.…,N-L,N+1,) 光栅的分辨本领: R=mN 5X射线的衍射 主极大满足布喇格公式:2dsn0=k元,(k=1,2,3) 其中:d为相邻晶面的间距,p为掠射角。 光的偏振部分: 1偏振光 )线偏振光:在垂直于光传播方向的平面内光矢量只沿一个固定方向振动,即光矢量的 端点的轨迹是一直线。 2)椭圆(圆)偏振光:在垂直于光传播方向的平面内,光矢量端点的轨迹是一椭圆(圆): 迎着光看,光矢量逆时针旋转,称为左旋椭圆(圆)偏振光:顺时针旋转则称为右旋椭 圆(圆)偏振光。 3)部分偏振光的偏振度 p=1*: 其中:p为偏振光的光强:m为自然光的光强 4)线偏振光的获取 可以用多中方法产生线偏振光,最常用的方法是让自然光透过偏振片产生线偏振光 当光强为的自然光照射偏振片时,出射光的光强为 1。 2马吕斯定律 光强为6的线偏振光通过一块偏振片,若光矢量与偏振片的起偏方向夹角为,不考 虑吸收,则出射光光强为 1=1o cos'a 其中:α为线偏振光的偏振方向与偏振片的偏振化方向间的夹角。 3布儒斯特定律 26
教案 第十七章 波动光学 269 m m a d = 时,m,2m,3m,…级明纹将不出现,这就是缺级现象。 暗纹条件: N(a + b)sin = ma, (m =1,2,3, , N −1, N +1, ) 光栅的分辨本领: R = mN 5 X 射线的衍射 主极大满足布喇格公式: 2d sin = k, (k =1,2,3, ) 其中:d 为相邻晶面的间距,为掠射角。 光的偏振部分: 1 偏振光 1) 线偏振光:在垂直于光传播方向的平面内光矢量只沿一个固定方向振动,即光矢量的 端点的轨迹是一直线。 2) 椭圆(圆)偏振光:在垂直于光传播方向的平面内,光矢量端点的轨迹是一椭圆(圆)。 迎着光看,光矢量逆时针旋转,称为左旋椭圆(圆)偏振光;顺时针旋转则称为右旋椭 圆(圆)偏振光。 3) 部分偏振光的偏振度 P n P I I I P + = 其中:IP 为偏振光的光强;In 为自然光的光强。 4) 线偏振光的获取 可以用多中方法产生线偏振光,最常用的方法是让自然光透过偏振片产生线偏振光, 当光强为 I0 的自然光照射偏振片时,出射光的光强为 0 2 1 I = I 2 马吕斯定律 光强为 I0 的线偏振光通过一块偏振片,若光矢量与偏振片的起偏方向夹角为,不考 虑吸收,则出射光光强为 2 0 I = I cos 其中:为线偏振光的偏振方向与偏振片的偏振化方向间的夹角。 3 布儒斯特定律

教案第十七章波动光学 光向两种介质的界面上入射,当入射角为布儒斯特角时,反射光为垂直入射面振 动的线偏振光,其中6满足 tani, 此时反射光与折射光之间的夹角为π2,即6+90°。 4双折射 )双折射现象:一束自然光射入各向异性晶体分为两束光线,遵从折射定律的那束光线 称为o光,不遵从折射定律的那束光线称为©光。O光和e光都是线偏振光。 2)光轴:在各向异性晶体内有一确定的方向,光沿这个方向传播时不发生双折射,这个 方向称为晶体的光轴。只有一个光轴的晶体称为单轴晶体。 3)光线的主平面:品体内由一条光线和晶体光轴确定的平面叫这条光线的主平面。0光 的振动垂直于。光的主平面,©光的振动在©光的主平面内。入射面含有光轴时,两 个主平面重合,0光的振动在©光的主平面内。入射面含有光轴时,两个主平面重合, 0光振动与e光振动相互垂直。光轴与入射面不平行时,两个主平面不重合,c光一 般不在入射面内,此时o光振动和e光振动也不垂直。 5波片 从单轴品体上切割下来的平行平面薄片,光轴平行于品面。当入射线偏振光的振动 方向与光轴有一夹角a时,在晶体内发生双折射,产生0光和e光。当光线垂直入射波片 时,在晶体内分成0光和©光,它们传播方向相同(都沿入射光方向)、振动方向相互垂 直,传播速度不同(因为折射率不同)。通过厚度为d的晶片后,o光和e光通过波片后 的光程差为 4=(n。-n.)d 能使光程差4=k从+子,《=012,3)的波片叫做二分之一波片:能使光程差 4经+ ,(k=0,1,2,3,)为的波片叫做四分之一波片。2/2、4片都是相对某一确定 波长而言的。 用四分之一波片把线偏振光变成椭圆(圆)偏振光:用二分之一波片改变线偏振光 的振动方向。 §1相干光Coherent light 1光矢量 270
教案 第十七章 波动光学 270 光向两种介质的界面上入射,当入射角为布儒斯特角 ib 时,反射光为垂直入射面振 动的线偏振光,其中 ib 满足 1 2 tan n n i b = 此时反射光与折射光之间的夹角为/2,即 ib+=900。 4 双折射 1) 双折射现象:一束自然光射入各向异性晶体分为两束光线,遵从折射定律的那束光线 称为 o 光,不遵从折射定律的那束光线称为 e 光。O 光和 e 光都是线偏振光。 2) 光轴:在各向异性晶体内有一确定的方向,光沿这个方向传播时不发生双折射,这个 方向称为晶体的光轴。只有一个光轴的晶体称为单轴晶体。 3) 光线的主平面:晶体内由一条光线和晶体光轴确定的平面叫这条光线的主平面。o 光 的振动垂直于 o 光的主平面,e 光的振动在 e 光的主平面内。入射面含有光轴时,两 个主平面重合,o 光的振动在 e 光的主平面内。入射面含有光轴时,两个主平面重合, o 光振动与 e 光振动相互垂直。光轴与入射面不平行时,两个主平面不重合,e 光一 般不在入射面内,此时 o 光振动和 e 光振动也不垂直。 5 波片 从单轴晶体上切割下来的平行平面薄片,光轴平行于晶面。当入射线偏振光的振动 方向与光轴有一夹角时,在晶体内发生双折射,产生 o 光和 e 光。当光线垂直入射波片 时,在晶体内分成 o 光和 e 光,它们传播方向相同(都沿入射光方向)、振动方向相互垂 直,传播速度不同(因为折射率不同)。通过厚度为 d 的晶片后,o 光和 e 光通过波片后 的光程差为 = (no − ne )d 能使光程差 , ( 0,1,2,3, ) 2 = k + k = 的波片叫做二分之一波片;能使光程差 , ( 0,1,2,3, ) 2 4 = + k = k 为的波片叫做四分之一波片。/2、/4 片都是相对某一确定 波长而言的。 用四分之一波片把线偏振光变成椭圆(圆)偏振光;用二分之一波片改变线偏振光 的振动方向。 §1 相干光 Coherent light 1. 光矢量
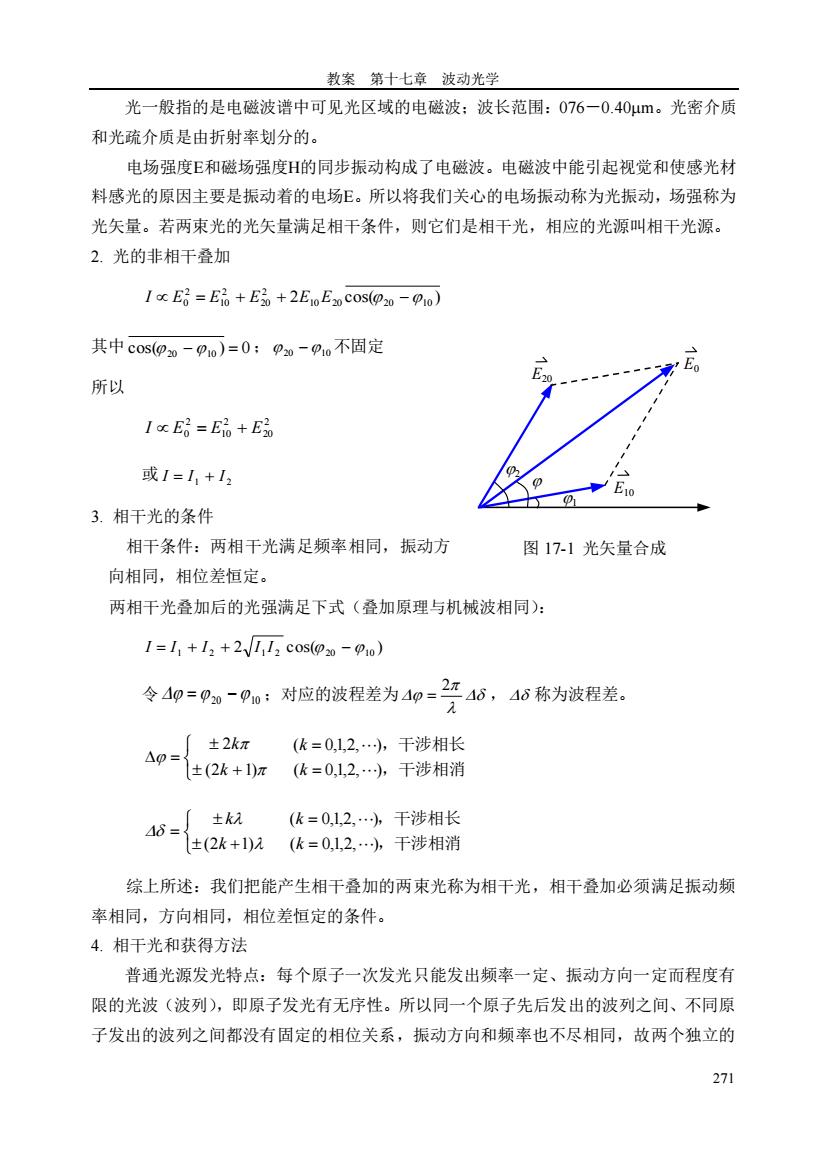
教案第十七章波动光学 光一般指的是电磁波谱中可见光区域的电磁波:波长范围:076-0.40μm。光密介质 和光疏介质是由折射率划分的。 电场强度E和磁场强度H的同步振动构成了电磁波。电磁波中能引起视觉和使感光材 料感光的原因主要是振动着的电场E。所以将我们关心的电场振动称为光振动,场强称为 光矢量。若两束光的光矢量满足相干条件,则它们是相干光,相应的光源叫相干光源。 2.光的非相干叠加 I E=Eio+E+2E1oEzo cos(2o-1o) 其中c0s00-po=0:-m不固定 所以 IcE路=E品+E 或1=11+12 3.相干光的条件 相干条件:两相干光满足频率相同,振动方 图17-1光矢量合成 向相同,相位差恒定。 两相干光叠加后的光强满足下式(叠加原理与机械波相同): 1=1+12+2√12cose0-po) 令4p=0-9:对应的波程差为4=46,46称为波程差。 [±2kπ (伏=01,2,干涉相长 △0=±2k+1x依=0,L2以干涉相消 46= 「±k2(k=0,1,2,…b干涉相长 ±(2k+)1(k=0,12干涉相消 综上所述:我们把能产生相干叠加的两束光称为相干光,相干叠加必须满足振动频 率相同,方向相同,相位差恒定的条件。 4.相干光和获得方法 普通光源发光特点:每个原子一次发光只能发出频率一定、振动方向一定而程度有 限的光波(波列),即原子发光有无序性。所以同一个原子先后发出的波列之间、不同原 子发出的波列之间都没有固定的相位关系,振动方向和频率也不尽相同,故两个独立的 271
教案 第十七章 波动光学 271 光一般指的是电磁波谱中可见光区域的电磁波;波长范围:076-0.40m。光密介质 和光疏介质是由折射率划分的。 电场强度E和磁场强度H的同步振动构成了电磁波。电磁波中能引起视觉和使感光材 料感光的原因主要是振动着的电场E。所以将我们关心的电场振动称为光振动,场强称为 光矢量。若两束光的光矢量满足相干条件,则它们是相干光,相应的光源叫相干光源。 2. 光的非相干叠加 2 cos( ) 10 20 20 10 2 20 2 10 2 I E0 = E + E + E E − 其中 cos( 20 −10 ) = 0 ; 20 −10 不固定 所以 2 20 2 10 2 I E0 = E + E 或 1 2 I = I + I 3. 相干光的条件 相干条件:两相干光满足频率相同,振动方 向相同,相位差恒定。 两相干光叠加后的光强满足下式(叠加原理与机械波相同): 2 cos( ) = 1 + 2 + 1 2 20 −10 I I I I I 令 = 20 − 10 ;对应的波程差为 2 = , 称为波程差。 ,干涉相消 ,干涉相长 ( 0,1,2, ) ( 0,1,2, ) (2 1) 2 = = + = k k k k ,干涉相消 ,干涉相长 ( 0,1,2, ) ( 0,1,2, ) (2 1) = = + = k k k k 综上所述:我们把能产生相干叠加的两束光称为相干光,相干叠加必须满足振动频 率相同,方向相同,相位差恒定的条件。 4. 相干光和获得方法 普通光源发光特点:每个原子一次发光只能发出频率一定、振动方向一定而程度有 限的光波(波列),即原子发光有无序性。所以同一个原子先后发出的波列之间、不同原 子发出的波列之间都没有固定的相位关系,振动方向和频率也不尽相同,故两个独立的 E10 E20 E0 1 2 图 17-1 光矢量合成

教案第十七章波动光学 普通光源发出的光不是相干光。 普通光源:白炽灯、钠光灯、太阳等光源,是相对激光而言的。 。分波阵面法:从同一波阵面上取出两部分作为相干光源,即用分光束获得相干光: 如杨氏实验等。 ·分振幅法:将一普通光源上同一点发出的光,利用反射或折射等方法使它“一分 为二”,沿两条不同的路径传播并相遇,这时原来的每一个波列都分成了频率相同、 振动方向相同,相位差恒定的两部分,当它们相遇时,就能产生干涉现象。其原 理是利用反射、折射把波面上某处的振幅分成两部分,再使它们相遇从而产生干 涉现象。如薄膜干涉等。 S2杨氏双缝干涉实验双镜劳埃德镜Coherentinstruments 一杨氏双缝干涉实验 图17-2杨氏双缝干涉条纹计算用图 由光源发出的光照射在单缝S上,使单缝S成为实施本实验的缝光源。在单缝S前 面放置两个相距很近的狭缝S和S,且S和S与S之间的距离均相等。S和是由同 一光源S形成的,满足振动方向相同、频率相同、相位差恒定的相干条件。故S和S为 相干光源。当S和S发出的光在空间相遇,将产生干涉现象,在屏幕P上将出现明、暗 交替的干涉条纹。 1.分波阵面获得相干光,满足振动方向相同,相位差恒定,频率相同的干涉条件。 2.干涉明暗条纹的位置 P点处的波程差 272
教案 第十七章 波动光学 272 普通光源发出的光不是相干光。 普通光源:白炽灯、钠光灯、太阳等光源,是相对激光而言的。 ⚫ 分波阵面法:从同一波阵面上取出两部分作为相干光源,即用分光束获得相干光; 如杨氏实验等。 ⚫ 分振幅法:将一普通光源上同一点发出的光,利用反射或折射等方法使它“一分 为二”,沿两条不同的路径传播并相遇,这时原来的每一个波列都分成了频率相同、 振动方向相同,相位差恒定的两部分,当它们相遇时,就能产生干涉现象。其原 理是利用反射、折射把波面上某处的振幅分成两部分,再使它们相遇从而产生干 涉现象。如薄膜干涉等。 §2 杨氏双缝干涉实验 双镜 劳埃德镜 Coherent instruments 一 杨氏双缝干涉实验 由光源发出的光照射在单缝 S 上,使单缝 S 成为实施本实验的缝光源。在单缝 S 前 面放置两个相距很近的狭缝 S1 和 S2,且 S1 和 S2 与 S 之间的距离均相等。S1 和 S2 是由同 一光源 S 形成的,满足振动方向相同、频率相同、相位差恒定的相干条件。故 S1 和 S2 为 相干光源。当 S1 和 S2 发出的光在空间相遇,将产生干涉现象,在屏幕 P 上将出现明、暗 交替的干涉条纹。 1. 分波阵面获得相干光,满足振动方向相同,相位差恒定,频率相同的干涉条件。 2. 干涉明暗条纹的位置 P 点处的波程差 0 x x x0 I S2 S1 x r2 r1 P x D d 图 17-2 杨氏双缝干涉条纹计算用图

教案第十七章波动光学 46=5,-片,(空气的折射率m=1) 在D>d,D>>x,即8很小时 6=5-h*dsn0≈dtan0= D (其中m0=若) )双缝干涉的明暗纹条纹 2)干涉明暗纹的位置 明纹x=kD2,k=012 d 暗纹=40k+受k=02 两相邻明纹或暗纹的间距都是4r=D3 d 其它x点的亮度介于明纹和暗纹之间,逐渐变化 综上所述,杨氏双缝干涉的特点: 1)用分振幅法获得相干光,两束光初相位相同,均无半波损失: 2)干涉明暗纹是等间距分布,相邻明纹间的距离与入射光的波长成正比,波长越小, 条纹间距越小: 3)若用白光照射,则在中央明纹(白光)的两侧将出现彩色条纹。 二杨氏双缝干涉的光强分布 狭缝S和S发出的光波单独到达屏上任一点B处的振幅分别为A和A2,光强分别 为山和2,则根据叠加原理,两光波叠加后的振幅为: A=V4++2A4,cos@2-m,) 两光波叠加后的光强为: 1=1,+12+2VT2cosp2-9) 273
教案 第十七章 波动光学 273 2 1 = r − r ,(空气的折射率 n= 1 ) 在 D >>d , D>>x,即 很小时 D xd = r2 − r1 d sin d tan = (其中 D x tan = ) 1) 双缝干涉的明暗纹条纹 暗纹 干涉相消 明纹 干涉相长 0,1,2, 0,1,2, (2 1) = = + = = k k k k x D d 2) 干涉明暗纹的位置 0,1,2, 2 (2 1) 0,1,2, = + = = = k d D x k k d D x k 暗纹 , 明纹 , 两相邻明纹或暗纹的间距都是 d D x = 其它 x 点的亮度介于明纹和暗纹之间,逐渐变化 综上所述,杨氏双缝干涉的特点: 1) 用分振幅法获得相干光,两束光初相位相同,均无半波损失; 2) 干涉明暗纹是等间距分布,相邻明纹间的距离与入射光的波长成正比,波长越小, 条纹间距越小; 3) 若用白光照射,则在中央明纹(白光)的两侧将出现彩色条纹。 二 杨氏双缝干涉的光强分布 狭缝 S1 和 S2 发出的光波单独到达屏上任一点 B 处的振幅分别为 A1 和 A2,光强分别 为 I1 和 I2,则根据叠加原理,两光波叠加后的振幅为: 2 cos( ) 1 2 2 1 2 2 2 A = A1 + A + A A − 两光波叠加后的光强为: 2 cos( ) = 1 + 2 + 1 2 2 −1 I I I I I

教案第十七章波动光学 其中:9,-9=2 -3入 -21 -A 2人 图17-3杨氏双缝干涉光强分布 当41=A2=40,则1=h=0,两光波叠加后的光强为 明纹k=012..光器1=4 暗纹k=0,12,…光强1=0 图17-4空间相干性 三缝宽对干涉条纹的影响空间相干性 在双缝干涉实验中,如果逐渐增加光源狭缝S的宽度,则屏幕P上的条纹和会变得 逐渐模糊起来,最后干涉条纹完全消失。这是因为单缝S内所包含的各小部分S'、S“等 非相干波源:它们互不相干,且S发出的光与S“发出的光通过双缝到达点B的波程差并 不相等,即S、S“发出的光将各自满足不同的干涉条件。比如,当S‘发出的光经过双缝 后恰在点B形成干涉极大的光强时,S"发出的光可能在点B形成干涉较小的光强。由于 274
教案 第十七章 波动光学 274 其中: 2 − 1 = 2 。 当A1=A2=A0,则I1=I2=I0,两光波叠加后的光强为 0,1,2, 0 0,1,2, 4 (2 1) 0 = = = = + = k I k I I k k 暗纹 光强 明纹 光强 三 缝宽对干涉条纹的影响 空间相干性 在双缝干涉实验中,如果逐渐增加光源狭缝 S 的宽度,则屏幕 P 上的条纹和会变得 逐渐模糊起来,最后干涉条纹完全消失。这是因为单缝 S 内所包含的各小部分 S 、S 等 非相干波源;它们互不相干,且 S 发出的光与 S 发出的光通过双缝到达点 B 的波程差并 不相等,即 S 、S 发出的光将各自满足不同的干涉条件。比如,当 S 发出的光经过双缝 后恰在点 B 形成干涉极大的光强时,S 发出的光可能在点 B 形成干涉较小的光强。由于 −3 −2 − O 2 3 4I0 I 2I0 I0 图 17-3 杨氏双缝干涉光强分布 S2 S1 O1 B O d r2 r1 S S S P 图 17-4 空间相干性

教案第十七章波动光学 S'、S“是非相干光源,它们在点B形成的合光强只是上述结果的简单相加,即非相干叠 加。所以,缝S愈宽,所包含的非相干子波源愈多,合光强的分布就愈偏离图17-的样式, 结果是最暗的光强不为零,使最亮和最暗的差别缩小,从而造成干涉条纹的模糊甚至消 失。只有当光源S的线度较小时,才能获得较清晰的干涉条纹,这一特性称为光场的空 间相干性。 强调:空间相干性是指光源不同位置发出的光在屏幕上形成的干涉条纹是非相干叠 加,是光源不同点的波列相遇在空间同一点;而时间相干性是指光源同一点发出的不同 时刻波列相遇在空间同一点,不能相干。 四双镜 图17-是双镜实验的示意图。点光源S发出的光经平面镜M、M反射到达屏P,这 两束光可以看成是分别由虚光源S和S发出的,而这两束光来自同一点光源,所以它们 是相干光。在它们相遇的区域将产生干涉现象。把屏幕P放到这区域中,就可以观察到 明暗相间的干涉条纹。 用研究杨氏双缝干涉实验类似的方法(几何方法),可以求出S和S之间的距离d 以及S和到屏P的距离d,并进而对干涉条纹作出计算。 双镜干涉实验的特点: 1.两束相干光可看作是由虚光源S1,S2发出: 2.两虚光源相位相同,可比作杨氏双缝干涉实验中的两个狭缝: 3.两束光均有半波损失: 4.重叠区形成条纹,条纹对两虚光源不对称。 五劳埃德镜 劳埃德镜实验不但显示了光的干涉现象,而且还显示了当光由光速较大(折射率较 小)的介质射向光速较小(折射率较大)的介质时,反射光的相位发生了跃变。 从狭缝S发出的光,一部分直接射到屏幕上,另一部分掠射到反射角M上,反射后 到达屏幕上。反射光可看成是由虚光源发出的。S和S2构成一对相干光源。图中阴影 区域表示叠加的区域,在屏幕上可以观察到明暗相间的干涉条纹。 若把屏幕放到和镜面相接触的P'位置,此时从S,和S2发出的光到达接触点L的路程 相等,在L处似乎应出现明纹,但是实验事实是,在接触处为一暗纹。这表明,直接射 到屏幕上的光与由镜面反射出来的光在L处的相位相反,即相位差为π。由于入射光的相 位没有变化,只能是反射光的相位跃变了π。 275
教案 第十七章 波动光学 275 S 、S 是非相干光源,它们在点 B 形成的合光强只是上述结果的简单相加,即非相干叠 加。所以,缝 S 愈宽,所包含的非相干子波源愈多,合光强的分布就愈偏离图 17-的样式, 结果是最暗的光强不为零,使最亮和最暗的差别缩小,从而造成干涉条纹的模糊甚至消 失。只有当光源 S 的线度较小时,才能获得较清晰的干涉条纹,这一特性称为光场的空 间相干性。 强调:空间相干性是指光源不同位置发出的光在屏幕上形成的干涉条纹是非相干叠 加,是光源不同点的波列相遇在空间同一点;而时间相干性是指光源同一点发出的不同 时刻波列相遇在空间同一点,不能相干。 四 双镜 图 17-是双镜实验的示意图。点光源 S 发出的光经平面镜 M1、M2 反射到达屏 P,这 两束光可以看成是分别由虚光源 S1 和 S2 发出的,而这两束光来自同一点光源,所以它们 是相干光。在它们相遇的区域将产生干涉现象。把屏幕 P 放到这区域中,就可以观察到 明暗相间的干涉条纹。 用研究杨氏双缝干涉实验类似的方法(几何方法),可以求出 S1 和 S2 之间的距离 d 以及 S1 和 S2 到屏 P 的距离 d ,并进而对干涉条纹作出计算。 双镜干涉实验的特点: 1. 两束相干光可看作是由虚光源 S1, S2 发出; 2. 两虚光源相位相同,可比作杨氏双缝干涉实验中的两个狭缝; 3. 两束光均有半波损失; 4. 重叠区形成条纹,条纹对两虚光源不对称。 五 劳埃德镜 劳埃德镜实验不但显示了光的干涉现象,而且还显示了当光由光速较大(折射率较 小)的介质射向光速较小(折射率较大)的介质时,反射光的相位发生了跃变。 从狭缝 S1 发出的光,一部分直接射到屏幕上,另一部分掠射到反射角 M 上,反射后 到达屏幕上。反射光可看成是由虚光源 S2 发出的。S1 和 S2 构成一对相干光源。图中阴影 区域表示叠加的区域,在屏幕上可以观察到明暗相间的干涉条纹。 若把屏幕放到和镜面相接触的 P位置,此时从 S1和 S2 发出的光到达接触点 L 的路程 相等,在 L 处似乎应出现明纹,但是实验事实是,在接触处为一暗纹。这表明,直接射 到屏幕上的光与由镜面反射出来的光在 L 处的相位相反,即相位差为。由于入射光的相 位没有变化,只能是反射光的相位跃变了