
教案第九章静电场中的导体和电介质 第九章静电场中的导体和电介质Dielectrics and conductor in electric field §1静电场中的导体conductor in electric field 1.导体的静电平衡条件 Eo 1)导体内部任一点的场强为零。 导体内部的合场强 2)导体表面上任一点的场强都与该点表面 垂直。若用电势来表述:对导体上任何两 汇E中 -- E=E。+E'=0 点a和b有 上导作 此时达到静电平衡 状态 y。-=E.d=0 即:导体是个等势体,表面为一等势面。 2.静电平衡条件下,导体上电荷的分布 1)外于静电平衡的导体,其电荷只分布于外表面上。此结论 图1 图2腔内有电荷 图3腔内无电荷 可由高斯定理来验证,,当导体内有空腔时,其情形则分别为图2及图3。 2)电荷面密度与场强的关系 图4是放大的导体表面,因为导体内电场为零,导体表面上的电场与表面垂直,则 作如图所示的高斯面可得: Ed=g·dr E=(1) 80 80 (1)式即为电场与导体的电荷面密度关系。 3)曲率半径与电荷面密度的关系 E-0 160 图4放大的导体表面
教案 第九章 静电场中的导体和电介质 160 第九章 静电场中的导体和电介质 Dielectrics and conductor in electric field §1 静电场中的导体 conductor in electric field 1. 导体的静电平衡条件 1)导体内部任一点的场强为零。 2)导体表面上任一点的场强都与该点表面 垂直。若用电势来表述:对导体上任何两 点 a 和 b 有 − = d = 0 b a a b V V E l 即:导体是个等势体,表面为一等势面。 2. 静电平衡条件下,导体上电荷的分布 1) 外于静电平衡的导体,其电荷只分布于外表面上。此结论 可由高斯定理来验证,,当导体内有空腔时,其情形则分别为图 2 及图 3。 2)电荷面密度与场强的关系 图 4 是放大的导体表面,因为导体内电场为零,导体表面上的电场与表面垂直,则 作如图所示的高斯面可得: 0 0 d d = = E s E s (1) (1)式即为电场与导体的电荷面密度关系。 3)曲率半径与电荷面密度的关系 E0 E 导体 导体内部的合场强 E = E0 + E = 0 此时达到静电平 衡 状态 S E=0 图 1 -q +q 图 2 腔内有电荷 图 3 腔内无电荷 dS E=0 导体 图 4 放大的导体表面 E
教案第九章静电场中的导体和电介质 对两个孤立导体,有 V= 194= 192 4π6,R4π6,R2 =R=深 图5两孤立导体 r公o风-风 即:电荷面密度与曲率半径成反比。 '.Exco 根据上述结论,对一个非球形的带电体,其电荷分布应为下图所示。 + ++ 十 + 图6导体表面电荷分布情况 3.尖端放电现象 尖端导体的面密度大,从而其电场可大到使周围的空气电离面引起放电的程度,此 即尖端放电现象。 讲解避雷针的工作原理,此处可加一演示实验。 4.静电屏蔽 外屏敲 内屏蔽 图7静电屏蔽
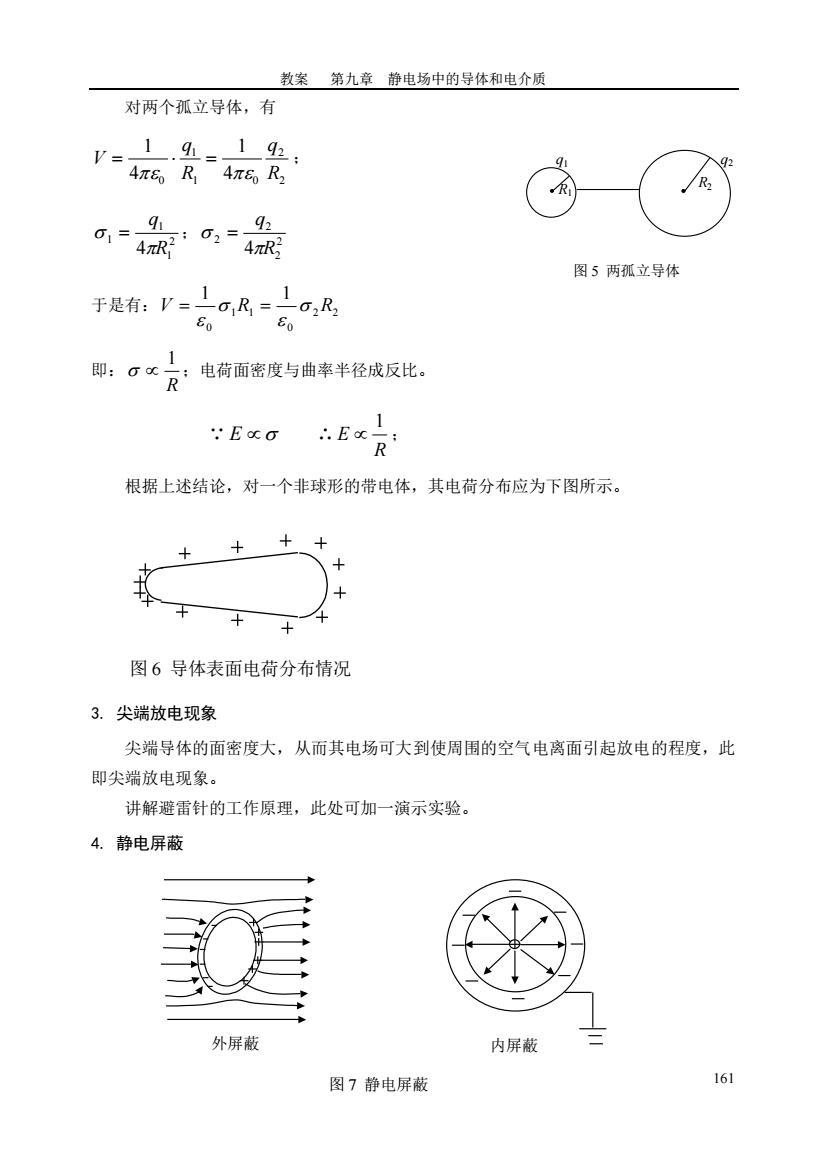
教案 第九章 静电场中的导体和电介质 161 对两个孤立导体,有 2 2 1 0 1 0 4 1 4 1 R q R q V = = ; 2 1 1 1 4 R q = ; 2 2 2 2 4 R q = 于是有: 2 2 0 1 1 0 1 1 V R R = = 即: R 1 ;电荷面密度与曲率半径成反比。 ∵ E ∴ R E 1 ; 根据上述结论,对一个非球形的带电体,其电荷分布应为下图所示。 3. 尖端放电现象 尖端导体的面密度大,从而其电场可大到使周围的空气电离面引起放电的程度,此 即尖端放电现象。 讲解避雷针的工作原理,此处可加一演示实验。 4. 静电屏蔽 R1 R2 q1 q2 图 5 两孤立导体 图 6 导体表面电荷分布情况 外屏蔽 内屏蔽 图 7 静电屏蔽

教案第九章静电场中的导体和电介质 5.高压带电作业 静电屏蔽的一个具体应用。 例:己知:R、R、R、q(球和球壳均带正电q),求:电荷 如何分布,球心处电势。解:由导体的性质分析:可知,内球 外表面q,球壳内表面-q,外表面2g =E.7=91-⊥+2 切6见元+龙):分段积 §2电容、电容器Capacitance,.Capacitor 1.电容 定义:C-号:孤立号体所带电最与其电势的比值。 单位:法拉a)1F-长 1F=106F=102PF 2.电容器 0 定义:两个带有等值而异号电荷的导体所组成的 C- 系统。 1)平板电容器 --Ei=Ed=品4 d C-VA-V8 (1) d 2)圆柱形电容器 单位长度带电为: 1 其间电场E为: 162
教案 第九章 静电场中的导体和电介质 162 5. 高压带电作业 静电屏蔽的一个具体应用。 例:已知:R1、R2、R3、q(球和球壳均带正电 q),求:电荷 如何分布,球心处电势。解:由导体的性质分析:可知,内球 外表面 q,球壳内表面-q,外表面 2q。 ) 1 1 2 ( 4 d 0 3 2 1 0 0 R R R q V = E l = − + ;分段积 §2 电容、电容器 Capacitance, Capacitor 1. 电容 定义: V Q C = ;孤立导体所带电量与其电势的比值, 单位:法拉(Farad) V C F 1 1 1 = ; F F PF 6 12 1 =10 =10 2. 电容器 定义:两个带有等值而异号电荷的导体所组成的 系统。 1)平板电容器 d S Q V V E dl E d B A A B − = = = 0 d S V V Q C A B 0 = − = (1) 2)圆柱形电容器 单位长度带电为: l Q = 其间电场 E 为: R3 R1 R2 q q V1 V2 +Q -Q V1 V2 Q C − = +Q -Q A B d B A r R -Q +Q
教案第九章静电场中的导体和电介质 E 1 227 --医品9 C 2π61 V4-V。-hRr (2) 若以d表示两圆柱体间距离,则有: (2)式变为: C÷2m-26r- d (3) d d 此时,圆柱形电容器可视为平板电容器。 3)球形电容器 ⅓-6=品贫安 (4) 由式(1)、(2)、(4)可以看出,电容器的电容只与本身的 形状有关,与其带电量无关。 例:设有两根半径为a的平行长直导线,其中心相距为d,且db>a,求单位长度的电容: 解:设单位长度的电量为τ:则其间P点电场为: 01 日=生白)(说期:电场的宋都是先球 0 再迭加,认为电荷是均匀分布在表面上) 两导线之间的电势差为:
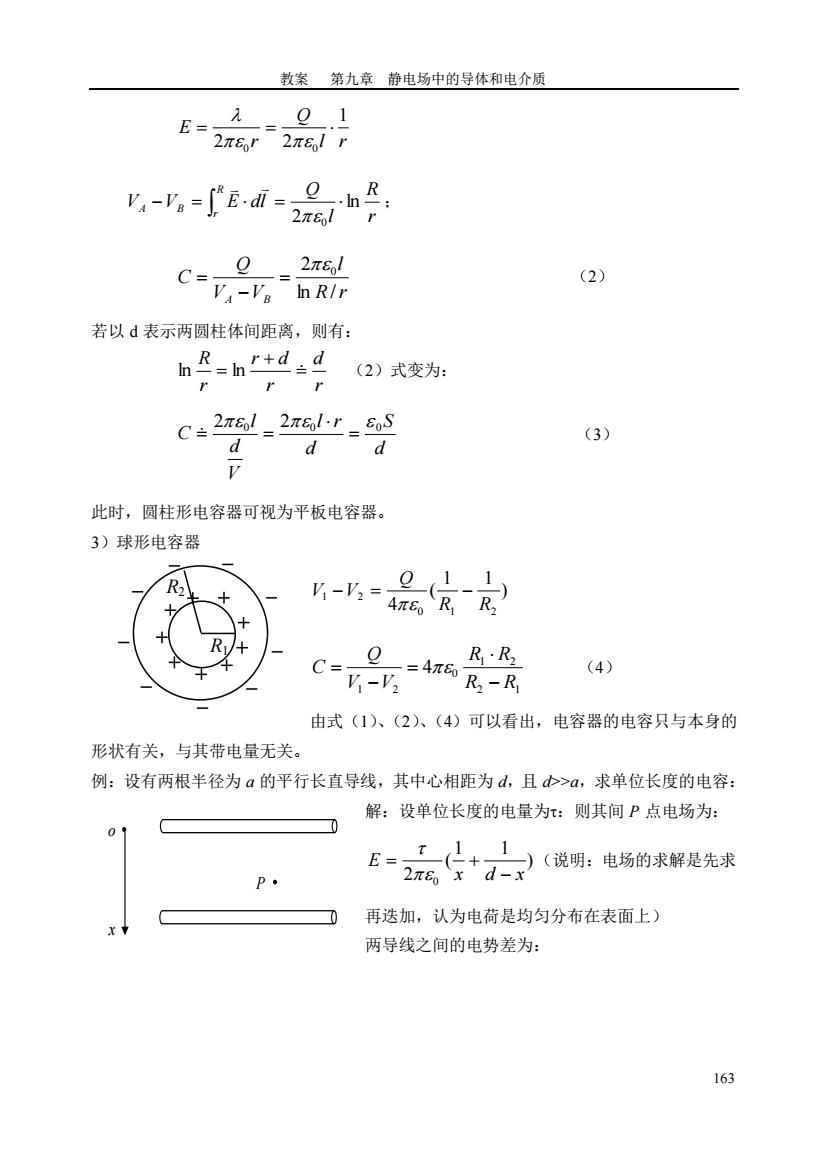
教案 第九章 静电场中的导体和电介质 163 l r Q r E 1 2 0 2 0 = = r R l Q V V E dl R r A B ln 2 0 − = = ; R r l V V Q C A B ln / 2 0 = − = (2) 若以 d 表示两圆柱体间距离,则有: r d r r d r R = + ln = ln (2)式变为: d S d l r V d l C 2 0 2 0 0 = = = (3) 此时,圆柱形电容器可视为平板电容器。 3)球形电容器 ) 1 1 ( 4 0 1 2 1 2 R R Q V −V = − 2 1 1 2 0 1 2 4 R R R R V V Q C − = − = (4) 由式(1)、(2)、(4)可以看出,电容器的电容只与本身的 形状有关,与其带电量无关。 例:设有两根半径为 a 的平行长直导线,其中心相距为 d,且 d>>a,求单位长度的电容: 解:设单位长度的电量为:则其间 P 点电场为: ) 1 1 ( 2 0 x d x E − = + (说明:电场的求解是先求 再迭加,认为电荷是均匀分布在表面上) 两导线之间的电势差为: R2 R1 P o x

教案第九章静电场中的导体和电介质 IInd-a=Imd(d>>a) = π6aEoa c号是 a 3.电容器的串、并联(不讲,自学) §3静电场中的电介质、电极化强度Dielectrics,Polarization 1.有电介质的电容器 两个相同的电容器,一个为真空,另一 个插入一电介质,实验得出:其电容量的关 系为: C=eC。 (1) 6,称为相对介电常数,6,为一大于1的常数。 6=6,6。称为介电常数或电容率: 由此实验知,插入电介质后,电容器的电容增大了。 2.电介质的极化 电极化强度,D、E、P之间的关系,(说明:在前面高斯定理中已经讲了D,这里 可如下讲解,见程教年修订版,如此讲要比马文蔚书中的讲解思路好一些。)须选先讲极 化机制,即有极分子和无极分子的极化机理。 1)电极化强度:单位体积中分子电偶极矩的矢量和,用P表示: (1)
教案 第九章 静电场中的导体和电介质 164 ln ln ( ) ) 1 1 ( 2 0 0 0 1 2 d a a d a d a dx x d x V V E dl d a a d a a = − = − − = = + − − ∴ a V V V d Q C ln 0 1 2 = − = = 3. 电容器的串、并联(不讲,自学) §3 静电场中的电介质、电极化强度 Dielectrics,Polarization 1. 有电介质的电容器 两个相同的电容器,一个为真空,另一 个插入一电介质,实验得出:其电容量的关 系为: C rCo = (1) r 称为相对介电常数, r 为一大于 1 的常数。 0 = r 称为介电常数或电容率; 由此实验知,插入电介质后,电容器的电容增大了。 2. 电介质的极化 电极化强度, D E P 、 、 之间的关系,(说明:在前面高斯定理中已经讲了 D ,这里 可如下讲解,见程教年修订版,如此讲要比马文蔚书中的讲解思路好一些。)须选先讲极 化机制,即有极分子和无极分子的极化机理。 1) 电极化强度:单位体积中分子电偶极矩的矢量和,用 P 表示 : V P P = (1) q Cr C + _

教案第九章静电场中的导体和电介质 实验证明:电极化强度P与电介质内的合场强E成正比,在国际单位制中,记作 P=y.EoE (2) 必是与电介质性质有关的比例系数,称电极化率,是 无单位量。 显然,电极化强度与极化电荷面密度。相联系 A 下面以平行板电容器为例,讨论其间关系。在介质 P E 中取一长为山,面积为△S的柱体,柱体内分子电偶 极矩矢量和大小为 ΣP=(oAS)d(相当于ql,9=△So', =d) P=p-(GnS)d (3) △Sd 2)0与'间的关系 由高斯定理知E,=g,E=g,E=g Eo 80 而E=E。-E即g=g-g:把6=E5,代入得: 6066 (4) 6, 因为6,>1,故束缚电荷面密度性小于自由电荷面密度。 3)D、E、P之间的关系 P=y.6E=σ':而o=6,6E代入(4)式得: y5,E=l-6,6E) 8, 则6,=1+ye 上式两边同乘6oE得:E=6E+yoE 金
教案 第九章 静电场中的导体和电介质 165 实验证明:电极化强度 P 与电介质内的合场强 E 成正比,在国际单位制中,记作 P ye E 0 = (2) ye是与电介质性质有关的比例系数,称电极化率,是 无单位量。 显然,电极化强度与极化电荷面密度 相联系, 下面以平行板电容器为例,讨论其间关系。在介质 中取一长为 d,面积为 S 的柱体,柱体内分子电偶 极矩矢量和大小为 P = (S)d (相当于 q l ,q = S, l=d) = = = Sd S d V P P ( ) (3) 2) 与 间的关系 由高斯定理知 0 0 E = ; 0 E = ; E = 而 E = E − E 0 即 0 0 = − ;把 r = 0 代入得: ) 1 (1 r = − (4) 因为 r 1 ,故束缚电荷面密度性小于自由电荷面密度。 3) D E P 、 、 之间的关系 ∵ P = y E = e 0 ;而 = r 0E 代入(4)式得: ) 1 y 0E (1 r 0E r e = − 则 r e = 1+ y 上式两边同乘 0E 得: E = 0E + y0 0E +0 -0 + - d E S E0 P

教案第九章静电场中的导体和电介质 即: D=6E+P (5) (5)式是D、E、P之间的普遍关系式,在一般的电场中也是成立的。 4)E与E。的关系: 1n三0-==-0-)o 80808060 808,8, (1)无极分子组成的电介质的极化:(位移极化) 无极分子的正负电荷中心在无外场时是重合的,见图1,在外电场作用下,其正负电 荷分离中心,形成电偶极矩,这些小的电偶极矩在外场中按一定的方向排列,从而使与 外场垂直的表面上出现正电荷和负电荷,这种电荷是不能脱离介质而单独存在的,故称 为束缚电荷或极化电荷,这种在外场作用下使介质表面出现极化电荷的现象称为电介质 的极化现象。 当外场撒去时,极化电荷消失,正负电荷中心又重合了。 图1 图2 图3 E (2)有极分子组成的电介质的极化:(取向极化) 有极分子的正负电荷中心不是重合的,其本身具有一定的固有偶极矩,故其极化过 程为上图中的后两个图。 上述两种极化,虽然微观机制不同,但宏观上均表现为在介质表面出现极化电荷 故在以后的讨论中,我们不在区分它们。 3.电极化强度矢量 用单位体积中分子电偶极矩的矢量和来表示电介质的极化程度: P= P △V
教案 第九章 静电场中的导体和电介质 166 即: D E P = 0 + (5) (5)式是 D E P 、 、 之间的普遍关系式,在一般的电场中也是成立的。 4) E 与 E0 的关系: r r r E E 0 0 0 0 0 0 0 ) 1 (1 1 ( ) 1 = = = − − = − = − (1)无极分子组成的电介质的极化:(位移极化) 无极分子的正负电荷中心在无外场时是重合的,见图 1,在外电场作用下,其正负电 荷分离中心,形成电偶极矩,这些小的电偶极矩在外场中按一定的方向排列,从而使与 外场垂直的表面上出现正电荷和负电荷,这种电荷是不能脱离介质而单独存在的,故称 为束缚电荷或极化电荷,这种在外场作用下使介质表面出现极化电荷的现象称为电介质 的极化现象。 当外场撤去时,极化电荷消失,正负电荷中心又重合了。 (2)有极分子组成的电介质的极化:(取向极化) 有极分子的正负电荷中心不是重合的,其本身具有一定的固有偶极矩,故其极化过 程为上图中的后两个图。 上述两种极化,虽然微观机制不同,但宏观上均表现为在介质表面出现极化电荷, 故在以后的讨论中,我们不在区分它们。 3. 电极化强度矢量 用单位体积中分子电偶极矩的矢量和来表示电介质的极化程度: V P P = 图 1 图 2 图 3 E

教案第九章静电场中的导体和电介质 P叫做电极化强度矢量,即电极化强度。 显然,电极化强度与极化电荷面密度σ'相联 系,下面以平板电容器为例,讨论其间关系。 在介质中取一长为d,面积为△S的柱体,其 底面的极化电荷密度分别为士σ'。 柱体内分子电偶极矩的矢量和大小为: P=(o',AS)d(相当于q1q=o△S=d) p=EP='Ad=a A△Sd (1) 说明:上式只是对平板电容器得出的结论: 对任意介质表面,则有σ'=P, 4.电介质中的场强E 见上图,介质中的E为E=E。+E',大小为E=E。-E则电压: U=E-d (2) 由电容定义式知:0-马面C=6,C,=6,5的 d ..U-2o=deo=d Eo (3) C ,EoS E, 由2)与()得:E= E,或E= (4) (4)式表明,插入电介质后,其间电场较原来减小了,这是由于极化场强与自由电荷场 强反向的原故。 §4电位移矢量,有介质时的高斯定理Dielectrics and Gauss'law 如图,取高斯面S,则 16
教案 第九章 静电场中的导体和电介质 167 P 叫做电极化强度矢量,即电极化强度。 显然,电极化强度与极化电荷面密度 相联 系,下面以平板电容器为例,讨论其间关系。 在介质中取一长为 d,面积为 S 的柱体,其 底面的极化电荷密度分别为 。 柱体内分子电偶极矩的矢量和大小为: P = ( S) d (相当于 q l q = S l=d) = = = Sd Sd V P P (1) 说明:上式只是对平板电容器得出的结论; 对任意介质表面,则有 P n = 4. 电介质中的场强 E 见上图,介质中的 E 为 E = E + E 0 ,大小为 E = E − E 0 则电压: U = E d (2) 由电容定义式知: U = C Q0 而 C d S r C r 0 0 = = ∴U = 0 0 0 0 E d r S dQ C Q r r = = (3) 由(2)与(3)得: 0 1 E E r = 或 r E E 0 = (4) (4)式表明,插入电介质后,其间电场较原来减小了,这是由于极化场强与自由电荷场 强反向的原故。 §4 电位移矢量,有介质时的高斯定理 Dielectrics and Gauss’ law 如图,取高斯面 S,则 +0 -0 + - d E S E0 P

教案第九章静电场中的导体和电介质 Es-@-0 (1) E.s=10。-Q E=1-g) (2) 前面得出: 8, 1=o-) 6,E060 即: 100=00-0 得: g'=,1-)或0°=0,1-) (3) (3)式即Q'与Q的关系。 由(1)、(2)看出,在由高斯定理求场强E时,需要首先知道σ'或Q',这样很不 方便,我们研究这项P.dS=「σ'·dS=oS=Q'代入(1)式得: fE西=0-fp 即: fE+1p5=o。 60 写为: (EE+P).dS=o 记D=E+P为电位移矢量。 上式可写为: D.ds=o (4) 168
教案 第九章 静电场中的导体和电介质 168 ( ) 1 0 0 E dS = Q − Q (1) ( ) 1 0 0 E S = Q − Q ( ) 1 0 0 E = − (2) 前面得出: 0 0 0 0 ; 1 E = E E = r ∴ ( ) 1 1 0 0 0 0 = − r 即: = − 0 0 1 r 得: ) 1 0 (1 r = − 或 ) 1 0 (1 r Q Q = − (3) (3)式即 Q 与 Q0 的关系。 由(1)、(2)看出,在由高斯定理求场强 E 时,需要首先知道 或 Q ,这样很不 方便,我们研究这项 P dS = dS = S = Q 代入(1)式得: ( ) 1 0 0 E dS = Q − P dS 即: 0 0 0 1 ) 1 (E + P dS = Q 写为: 0 0 ( E + P) dS =Q 记 D E P = 0 + 为电位移矢量。 上式可写为: D dS = Q0 (4) +0 -0 + - S E

教案第九章静电场中的导体和电介质 (4)式即为有电介质时的高斯定理,D,5为电位移通量,其一般表达式为: fD·ds=∑(Q) (5) 说明:上式虽然是从平板电容器中得出的,但可推广为一般情形。 D=8E+P=6E+a'=E+o,1- E。= D=E+6E1- ·.=6E+6E(G,-1) =5oE,E =gE 即: D=50E,E=sE (6) £=6o6,为介电介数。 说明:电位移矢量D为一辅助量,引入电位移矢量后,求解介质中的电场变得方便了, 但描写电场性质的物理量仍为电场强度E和电势V。 例1:如图:己知:S、d、h、6n、6n、Q,求C。 解:对介质1: fD.ds=AS. Sr---1 .+Q0 D.AS=OAS:D= d S D Co
教案 第九章 静电场中的导体和电介质 169 (4)式即为有电介质时的高斯定理, D dS 为电位移通量,其一般表达式为: i i D dS = (Q ) 0 (5) 说明:上式虽然是从平板电容器中得出的,但可推广为一般情形。 ) 1 0 0 0 0 (1 r D E P E E = + = + = + − ∵ 0 0 0 E = 1 0 E E = ∴ E E E E D E E r r r = = = + − = + − 0 0 0 0 0 0 ( 1) ) 1 (1 即: D rE E = = 0 (6) r = 0 为介电介数。 说明:电位移矢量 D 为一辅助量,引入电位移矢量后,求解介质中的电场变得方便了, 但描写电场性质的物理量仍为电场强度 E 和电势 V。 例 1:如图:已知:S、d1、d2、 r1 、 r2 、Q0 ,求 C。 解:对介质 1: = S Q D dS S 0 S Q S D S Q D S 0 0 = ; = S D Q E r r 1 0 1 0 0 1 = = +Q0 -Q0 r1 r2 d1 d2 S