
5.2 杂化轨道理论
5.2 杂化轨道理论

5.2.1杂化轨道理论的要点 >杂化轨道:在形成分子时, 能量相近 新轨道 杂化: 杂化轨道数 杂化轨道的形状,能量不同于原轨道,且重新 确定空间方向
5.2.1杂化轨道理论的要点 Ø杂化轨道:在形成分子时,同一原子中, 能量相近的原子轨道进行线性 组合,形成能量相同的新轨道。 杂化:上述过程叫杂化。 杂化轨道数 = 参加杂化的原子轨道数 如: sp杂化—s+p 杂化轨道数=2 杂化轨道的形状,能量不同于原轨道,且重新 确定空间方向
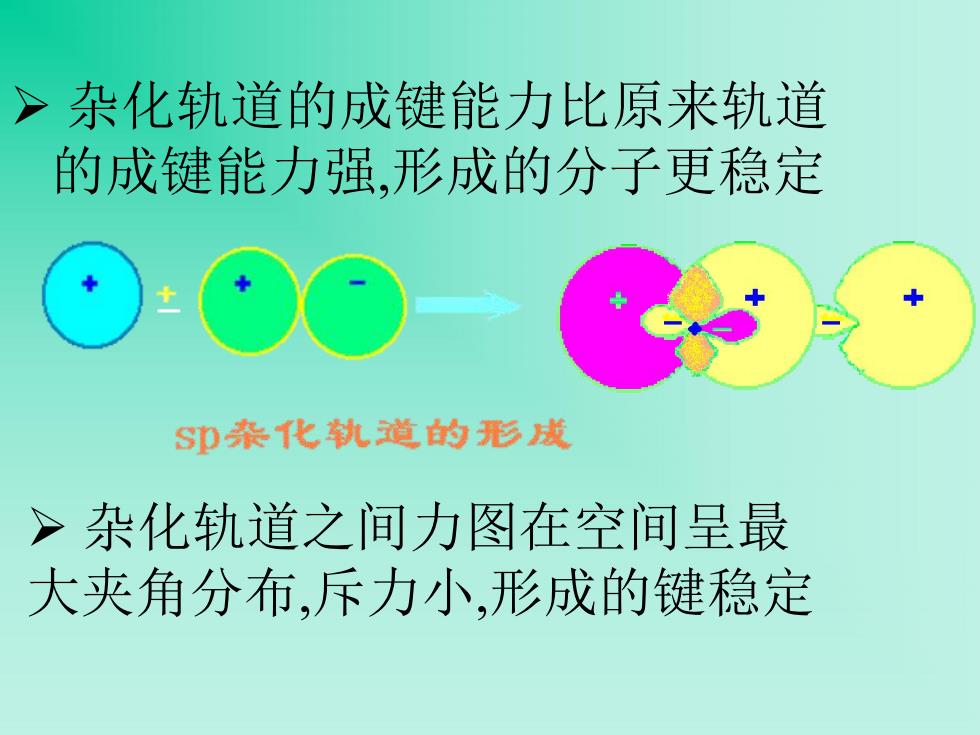
>杂化轨道的成键能力比原来轨道 的成键能力强,形成的分子更稳定 SD杂化轨道的形成 >杂化轨道之间力图在空间呈最 大夹角分布,斥力小,形成的键稳定
Ø 杂化轨道的成键能力比原来轨道 的成键能力强,形成的分子更稳定 Ø 杂化轨道之间力图在空间呈最 大夹角分布,斥力小,形成的键稳定 -

(sp) sp杂化 (b) (sp) sp杂化 (sp' (b) (sp) sp杂化 (sp (b】
sp杂化 sp 2杂化 sp 3杂化

5.2.2杂化轨道类型与分子的空间构型 Sp杂化 由一个ns轨道和一个np轨道杂化,形成 二个等同的Sp杂化轨道 Sp杂化特点:每个杂化轨道中含有7s轨道 成分和}p轨道成分;两条轨道 间的夹角为180°,呈直线形. 常见例子:BeC2,HgCl2,C02,C2H2等
5.2.2杂化轨道类型与分子的空间构型 sp杂化 由一个ns轨道和一个np轨道杂化,形成 二个等同的sp杂化轨道 sp杂化特点: 每个杂化轨道中含有 s 轨道 成分和 p轨道成分;两条轨道 间的夹角为180o ,呈直线形. 2 1 2 1 常见例子: BeCl2 , HgCl2 , CO2 , C2H2等

试说明BeCl2分子的空间构型 激发 杂化 成 2S2 2P 2P SP 2P 2个σ键 Be原子基态 激发态 杂化态 化合态 (sp) SP杂化形成直线型分子
试说明 BeCl2分子的空间构型 ↿ ⇂ Be原子基态 激发 ↑ ↑ 激发态 杂化 ↑ ↑ 杂化态 成键 ↿ ⇂ ↿ ⇂ 化合态 2S2 2P 2S 2P SP 2P 2个σ键 sp杂化形成直线型分子

$p2杂化 由一个ns轨道和二个np轨道杂化,形成 三个等同的$p2杂化轨道 Sp杂化特点:每个杂化轨道中会有s轨道 成分和子P轨道成分;三条轨道 间的夹角为120°,呈平面三角形. 常见例子:BF3,BC3,BBr3,C2H4等
sp2杂化 由一个ns轨道和二个np轨道杂化,形成 三个等同的sp2杂化轨道 sp 2杂化特点: 每个杂化轨道中含有 s 轨道 成分和 p轨道成分;三条轨道 间的夹角为120 o ,呈平面三角形. 3 1 3 2 常见例子: BF3 , BCl3 , BBr3 , C2H4 等

试说明BF3分子的空间构型 激发 1 杂化 个个 成使 oco 2S2 2P1 2S 2P SP2 2P 3个σ键 B原子基态 激发态 杂化态 化合态 B a (b
试说明 BF3分子的空间构型 ↿ ⇂ ↑ B原子基态 激发 ↑ ↑ ↑ 激发态 杂化 ↑ ↑ ↑ 成键 ↿ ⇂ ↿ ⇂ ↿ ⇂ 杂化态 化合态 2S2 2P1 2S 2P SP2 2P 3个σ键 平 面 正 三 角 形

sp3杂化 由一个ns轨道和三个np轨道杂化,形成 四个等同的sp3杂化轨道 Sp杂化特点:每个杂化轨道中会有s轨道 成分和p轨道成分四条轧道 间的夹角为10928,呈正四面体 常见例子:CH4,CCl4,C2H6,NH等
sp3杂化 由一个ns轨道和三个np轨道杂化,形成 四个等同的sp3杂化轨道 sp 3杂化特点: 每个杂化轨道中含有 s 轨道 成分和 p轨道成分;四条轨道 间的夹角为109 o28 ´ ,呈正四面体. 4 1 4 3 常见例子: CH4 , CCl4 , C2H6 , NH4 等

25+ 2p sp杂化形成正四面体分子
sp 3杂化形成正四面体分子