(四)自旋量子数(m、) 物理意义 决定电子的有旋方向 11 取值: 22 +符号:
(四)自旋量子数( ms ) 取值: 2 1 , 2 1 符号: ↑ , ↓ 物理意义: 决定电子的自旋方向 顺 时 针 逆 时 针
量子数组合和轨道数 主量子数 角量子数 磁量子数 波函数 同一电子层 n m 型 的轨道数 1,2,3 01,2. 0,士1,±2 ±( n2 1 0 0 Ψ1s 1 2 0 0 Ψ2S 4 1 0 型2pz 士1 W2Px 型2p
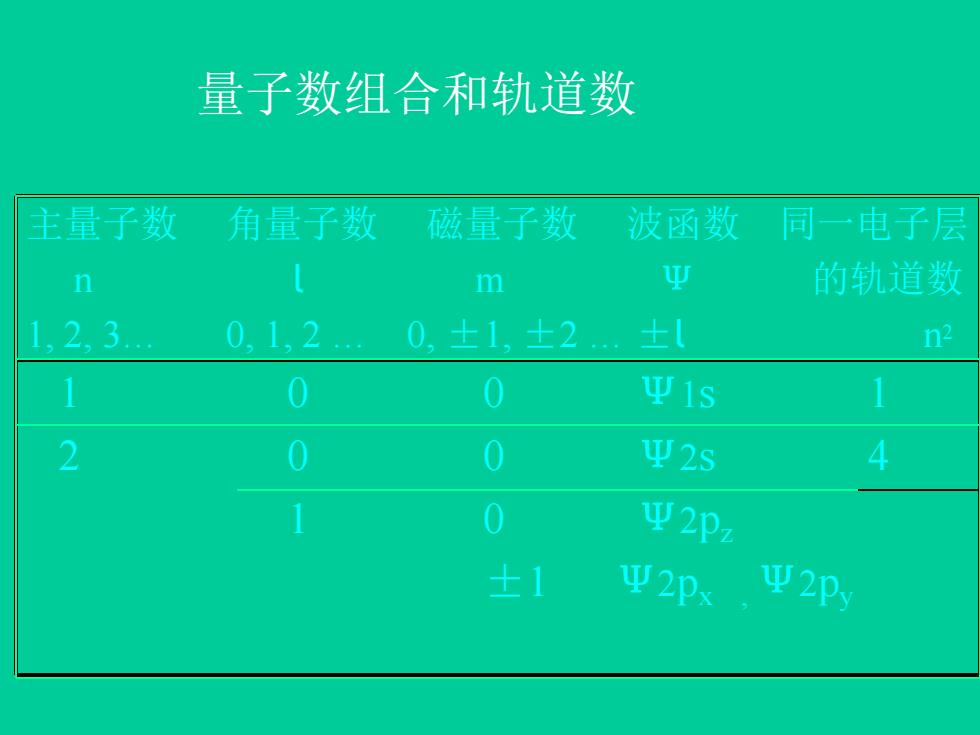
量子数组合和轨道数 主量子数 角量子数 磁量子数 波函数 同一电子层 n l m Ψ 的轨道数 1, 2, 3… 0, 1, 2 … 0, ±1, ±2 … ±l n2 1 0 0 Ψ1s 1 2 0 0 Ψ2s 4 1 0 Ψ2pz ±1 Ψ2px , Ψ2py
主量子数 角量子数 磁量子数 波函数 同一电子层 n m 型 的轨道数 1,2,3. 0.1.2. 0±1.±2± n2 3 0 0 Ψ3s 9 0 Ψ3pz ±1 Ψ3p Ψ3p 2 0 p3d,2 ±1 Ψ3dz. Ψ3dz ±2 Ψ3dy Ψ3d22
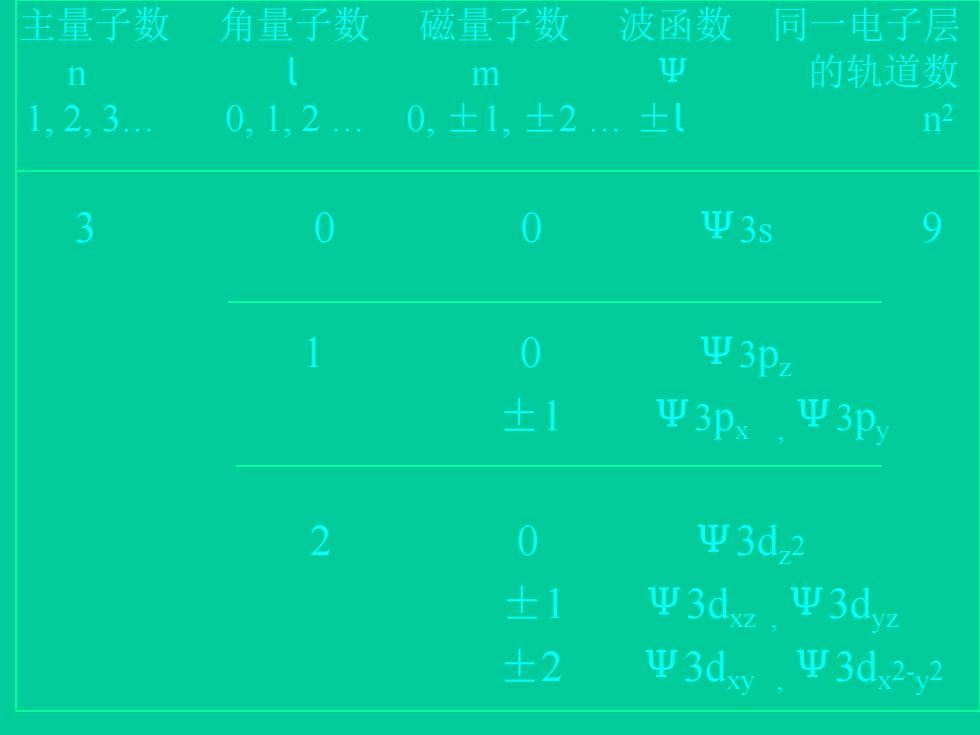
主量子数 角量子数 磁量子数 波函数 同一电子层 n l m Ψ 的轨道数 1, 2, 3… 0, 1, 2 … 0, ±1, ±2 … ±l n 2 3 0 0 Ψ3s 9 1 0 Ψ3pz ±1 Ψ3px , Ψ3py 2 0 Ψ3dz2 ±1 Ψ3dxz , Ψ3dyz ±2 Ψ3dxy , Ψ3dx 2-y 2

描述电子运动状态的总结 ◆三个量子数确定一个原子轨道(波函数): ψ1,0,0 称1s轨道 3,2,0 ψ3d 称3d轨道 ψ2,1,0 20 称2p轨道 ◆四个量子数可以描述一个电子的运动状态 原子中每个电子的运动状态可用四个量子数 来描述,四个量子数合理确定之后,每个电了 在核外空间的运动状态就确定了
描述电子运动状态的总结 三个量子数确定一个原子轨道(波函数): ψ1,0,0 = ψ1s 称1s轨道 ψ3,2,0 = ψ3d 称3d轨道 ψ2,1,0 = ψ2p 称2p轨道 原子中每个电子的运动状态可用四个量子数 来描述,四个量子数合理确定之后,每个电子 在核外空间的运动状态就确定了。 四个量子数可以描述一个电子的运动状态

每亚层中原子轨道的数目等于(2+1)个 ·在同一原子中,没有四个量子数完全相同 的电子.所以每条轨道最多只能容纳二个自 旋方向相反的电子. 每电子层具有轨道数为:n2 可能容纳的最多电子数为:2n2 n相同,l不同:Ens<Enp<End<Enf ◆L相同,n不同:E1s<E2s<E3s<E4s ◆一组,【值可确定一个能级
每亚层中原子轨道的数目等于(2l+1)个 在同一原子中,没有四个量子数完全相同 的电子.所以每条轨道最多只能容纳二个自 旋方向相反的电子. 每电子层具有轨道数为: n2 可能容纳的最多电子数为: 2n2 n 相同,l 不同 : Ens< Enp < E nd < E nf l 相同 , n不同 : E1s< E2s < E 3s< E 4s 一组 n, l 值可确定一个能级

例1:写出下列各能级或轨道的名称: 1)n=2【=1 2)n=3【=2 (3)n=5(=3 (4)n=2【=1m=-1 (5)n=4【=0m=0 (1)2p (2)3d (3)5f (4)2py (5)4s
例1: 写出下列各能级或轨道的名称: (1) n = 2 l = 1 (2) n = 3 l = 2 (3) n = 5 l = 3 (4) n = 2 l = 1 m = -1 (5) n = 4 l = 0 m = 0 解: (1) 2p (2) 3d (3) 5f (4) 2py (5) 4s