
第四章 原子结构和元素周期律
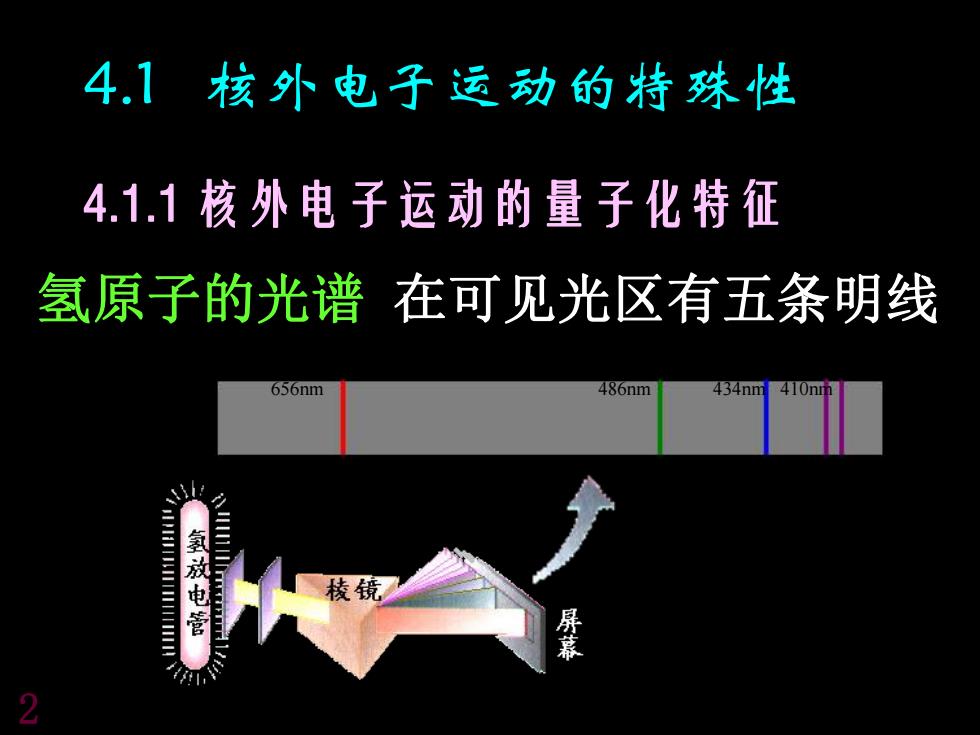
4.1核外电子运动的特殊性 4.1.1核外电子运动的量子化特征 氢原子的光谱在可见光区有五条明线 656nm 486nm 434nm40n w 氢放电管 棱镜 屏幕 2
4.1 核外电子运动的特殊性 4.1.1 核外电子运动的量子化特征 氢原子的光谱 在可见光区有五条明线 2 656nm 486nm 434nm 410nm
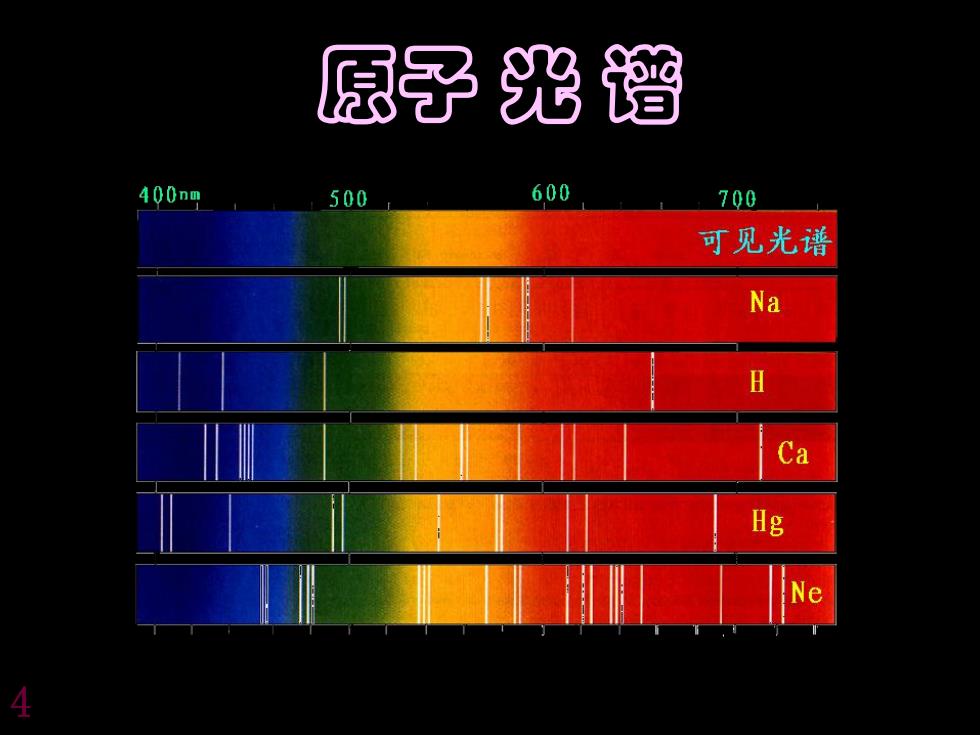
原子光谱 400nm 500 600 700 可见光谱 Na H Ca Hg Ne 4
原子 光 谱 4

父 玻尔理论(假说) 核外电子绕核在一定的轨道上运动, 具有一定的能量,称定态。 能量最低的定态叫 基态 基态(n=1),能量较高 的定态叫激发态(n>2) 激发为 此时电子运动的能量: -21.8×10 -18 E= 5 n
v 玻尔理论(假说) 能量最低的定态叫 基态(n=1),能量较高 的定态叫激发态(n>2)。 此时电子运动的能量: 5 核外电子绕核在一定的轨道上运动, 具有一定的能量,称定态。 ao J n 21.8 10 2 18 E

n=1.2.3.4.5..(正整数)一量子数 是不连续的 电子在不同定态下运动,其能量不同,处 在某一定态下的电子的能量有确定值。 电子获得能量后,由低能量定态(E) 跃迁到高能量定态(E,)。激发态不稳 定,瞬时恢复到基态(或能量较低的定
n=1.2.3.4.5…(正整数)—量子数 是不连续的 电子在不同定态下运动,其能量不同,处 在某一定态下的电子的能量有确定值。 电子获得能量后,由低能量定态(E1) 跃迁到高能量定态(E2)。激发态不稳 定,瞬时恢复到基态(或能量较低的定 6

态)—跃迁,同时辐 射出能量以光辐 红外光 射形式发射出来, 可见光 光子的能量为二 定态能量之差: hV =E2-E h=6.626×1034Js
态)—跃迁,同时辐 射出能量以光辐 射形式发射出来, 光子的能量为二 定态能量之差: hν=E2-E1 h = 6.626 × 10 -34 J· s 7

4.1.2核外电子运动的波粒二象性 >核外电子的运动完全不同于宏观物 体,不遵守经典力学规律 >1924年德布罗意(de Brog1id 所有微观粒子的运动也具有波 提出了一个德布罗意关系 h 入= m V
4.1.2 核外电子运动的波粒二象性 Ø 核外电子的运动完全不同于宏观物 体,不遵守经典力学规律 7 Ø 1924年德布罗意(de Broglie)提出假说: 所有微观粒子的运动也具有波粒二象性 Ø 提出了一个德布罗意关系式: p m h h λ

电子衍射实验证实了 德布罗意的假设。 晶体 电子源 ·电子的波性是大量电 子或少量电子的大量行 为的统计结果。 所以:物质波是概率波。 8
电子衍射实验证实了 德布罗意的假设。 电子的波性是大量电 子或少量电子的大量行 为的统计结果。 所以:物质波是概率波。 8 电子源 晶体