
第一章函数 一、本章学习要求与内容提要 (一)学习要求 1.理解函数的概念. 2.了解分段函数、基本初等函数、初等函数的概念, 3.了解反函数、复合函数的概念,会分析复合函数的复合结构. 4.会建立简单实际问题的函数模型 重点函数的概念、复合函数和初等函数的概念,会求函数的定 义域. 难点分段函数的概念,建立简单实际问题的函数模型. (二)内容提要 1.函数的定义 (1) 函数的定义 定义1设x和y是两个变量,D是一个给定的数集,如果对于每 个数x∈D,变量y按照一定法则总有惟一确定的数值与其对应,则称 y是x的函数,记作y=f(x).数集D称为该函数的定义域,x称为自变 量,y称为因变量
1 第一章 函数 一、本章学习要求与内容提要 (一)学习要求 1.理解函数的概念. 2.了解分段函数、基本初等函数、初等函数的概念. 3.了解反函数、复合函数的概念,会分析复合函数的复合结构. 4.会建立简单实际问题的函数模型. 重点 函数的概念、复合函数和初等函数的概念,会求函数的定 义域.难点 分段函数的概念,建立简单实际问题的函数模型. (二)内容提要 1.函数的定义 (1) 函数的定义 定义 1 设 x和 y 是两个变量, D是一个给定的数集,如果对于每 个数x D ,变量 y 按照一定法则总有惟一确定的数值与其对应,则称 y 是 x的函数,记作 y f (x) .数集D称为该函数的定义域, x称为自变 量, y 称为因变量

当自变量x取数值x时,因变量y按照法则f所取定的数值称为 函数y=f(x)在点x处的函数值,记作f(x).当自变量x遍取定义域D 的每个数值时,对应的函数值的全体组成的数集W=y=f(x,x∈D称 为函数的值域. 定义2设D与B是两个非空实数集,如果存在一个对应规则∫, 使得对D中任何一个实数x,在B中都有惟一确定的实数y与x对应, 则对应规则∫称为在D上的函数,记为 f:xy或f:D→B, y称为x对应的函数值,记为 y=f(x),x∈D, 其中,x称为自变量,y称为因变量 由定义2知,函数是一种对应规则,在函数y=f(x)中,∫表示函 数,(x)是对应于自变量x的函数值,但在研究函数时,这种对应关 系总是通过函数值表现出来的,所以习惯上常把在x处的函数值y称 为函数,并用y=f(x)的形式表示y是x的函数.但应正确理解,函数 的本质是指对应规则f.例如f(x)=x+4x2-10就是一个特定的函数, ∫确定的对应规则为 f()=()3+4()2-10 就是一个函数. (2) 函数的两要素
2 当自变量 x取数值 0 x 时,因变量 y 按照法则 f 所取定的数值称为 函数 y f (x)在点 0 x 处的函数值,记作 ( ) 0 f x .当自变量 x遍取定义域D 的每个数值时,对应的函数值的全体组成的数集W =y y f (x), x D称 为函数的值域. 定义 2 设D与B 是两个非空实数集,如果存在一个对应规则 f , 使得对D中任何一个实数 x,在B 中都有惟一确定的实数 y 与x 对应, 则对应规则 f 称为在D上的函数,记为 f : x y 或 f : D B , y 称为 x对应的函数值,记为 y f (x), x D , 其中, x称为自变量, y 称为因变量. 由定义 2 知, 函数是一种对应规则,在函数 y f (x)中, f 表示函 数, f (x)是对应于自变量 x的函数值,但在研究函数时,这种对应关 系总是通过函数值表现出来的,所以习惯上常把在x 处的函数值 y 称 为函数,并用 y f (x)的形式表示 y 是 x的函数.但应正确理解,函数 的本质是指对应规则 f .例如 ( 4 10 3 2 f x) x x 就是一个特定的函数, f 确定的对应规则为 ( ) ( ) 4( ) 10 3 2 f 就是一个函数. (2) 函数的两要素

函数y=f(x)的定义域D是自变量x的取值范围,而函数值y又是 由对应规则∫来确定的,所以函数实质上是由其定义域D和对应规则 ∫所确定的,因此通常称函数的定义域和对应规则为函数的两个要素. 也就是说,只要两个函数的定义域相同,对应规则也相同,就称这两 个函数为相同的函数,与变量用什么符号表示无关,如y=与:=√下, 就是相同的函数 2.函数的三种表示方法 (1) 图像法 用函数的图形来表示函数的方法称为函数的图像表示方法,简称 图像法.这种方法直观 性强并可观察函数的变化趋势,但根据函数图形所求出的函数值准确 度不高且不便于作理论研究. (2) 表格法 将自变量的某些取值及与其对应的函数值列成表格表示函数的方 法称为函数的表格表 示方法,简称表格法.这种方法的优点是查找函数值方便,缺点是数 据有限、不直观、不便于作理论研究. (3) 公式法
3 函数 y f (x) 的定义域 D 是自变量 x 的取值范围,而函数值 y 又是 由对应规则 f 来确定的,所以函数实质上是由其定义域D和对应规则 f 所确定的,因此通常称函数的定义域和对应规则为函数的两个要素. 也就是说,只要两个函数的定义域相同,对应规则也相同,就称这两 个函数为相同的函数,与变量用什么符号表示无关,如 2 y x与z v , 就是相同的函数. 2.函数的三种表示方法 (1) 图像法 用函数的图形来表示函数的方法称为函数的图像表示方法,简称 图像法.这种方法直观 性强并可观察函数的变化趋势,但根据函数图形所求出的函数值准确 度不高且不便于作理论研究. (2) 表格法 将自变量的某些取值及与其对应的函数值列成表格表示函数的方 法称为函数的表格表 示方法,简称表格法. 这种方法的优点是查找函数值方便,缺点是数 据有限、不直观、不便于作理论研究. (3) 公式法

用一个(或几个)公式表示函数的方法称为函数的公式表示方法, 简称公式法,也称为 解析法.这种方法的优点是形式简明,便于作理论研究与数值计算, 缺点是不如图像法来得直观. 在用公式法表示函数时经常遇到下面几种情况: ①分段函数 在自变量的不同取值范围内,用不同的公式表示的函数,称为分 段函数.如 x+1,x<0, f(x)= x2,0≤x<2, lnx,2≤x≤5, 就是一个定义在区间(-0,5]上的分段函数. ②用参数方程确定的函数 用参数方程 x=o(t) (tEI) y=w(t) 表示的变量x与y之间的函数关系,称为用参数方程确定的函数.例如 函数 y=1-x2(x∈[-1,)可以用参数方程y= cost sint (0≤t≤)表示. ③隐函数 如果在方程F(x,)=0中,当x在某区间I内任意取定一个值时, 相应地总有满足该
4 用一个(或几个)公式表示函数的方法称为函数的公式表示方法, 简称公式法,也称为 解析法. 这种方法的优点是形式简明,便于作理论研究与数值计算, 缺点是不如图像法来得直观. 在用公式法表示函数时经常遇到下面几种情况: 1 分段函数 在自变量的不同取值范围内,用不同的公式表示的函数,称为分 段函数.如 就是一个定义在区间( , 5]上的分段函数. ② 用参数方程确定的函数 用参数方程 ( ) ( ) y t x t (t Ι ) 表示的变量x与 y 之间的函数关系,称为用参数方程确定的函数.例如 函数 1 ( [ 1 ,1] ) 2 y x x 可以用参数方程 (0 ) sin cos t t t y 表示. 3 隐函数 如果在方程F(x, y) 0中,当 x 在某区间 I 内任意取定一个值时, 相应地总有满足该 ln , 2 5 , , 0 2 , 1 , 0, ( ) 2 x x x x x x f x

方程的惟一的y值存在,则称方程F(x,)=0在区间I内确定了一个隐 函数.例如方程e+y-1=0就确定了变量y是变量x之间的函数关系. 注意能表示成y=f(x)(其中f(x)仅为x的解析式)的形式的函数, 称为显函数.把 一个隐函数化成显函数的过程称为隐函数的显化.例如e+xy-1=0可 以化成显函数y=-.但有些隐函数确不可能化成显函数,例如 e+y-e'=0. 3.函数的四种特性 设函数y=∫x)的定义域为区间D,函数的四种特性如下表所示. 函数的四种特性表 函 数 的 定义 图像特点 特 性 设函数y=f(x)的定义域D关于原点对称,若对 偶函数 任意x∈D满足f(-x)=f(x),则称f(x)是D上的偶函 的图形关于 奇 数;若对任意x∈D满足f-)=-f(x),则称f(x)是D y轴对称;奇 偶 函数的图形 性 上的奇函数,既不是奇函数也不是偶函数的函数, 称为非奇非偶函数 关于原点对 称
5 方程的惟一的 y 值存在,则称方程F(x, y) 0在区间 I 内确定了一个隐 函数.例如方程e xy 1 0 x 就确定了变量 y 是变量 x之间的函数关系. 注意 能表示成 y f (x) (其中 f (x)仅为x的解析式)的形式的函数, 称为显函数. 把 一个隐函数化成显函数的过程称为隐函数的显化.例如e xy 1 0 x 可 以化成显函数 x y x 1 e .但有些隐函数确不可能化成显函数,例如 xy x e e 0 y . 3. 函数的四种特性 设函数 y f (x)的定义域为区间D,函数的四种特性如下表所示. 函数的四种特性表 函 数 的 特 性 定 义 图像特点 奇 偶 性 设函数 y f (x)的定义域D关于原点对称,若对 任意 x D满足 f (x) f (x),则称 f (x) 是D 上的偶函 数;若对任意x D满足 f (x) f (x),则称 f (x)是D 上的奇函数,既不是奇函数也不是偶函数的函数, 称为非奇非偶函数 偶 函 数 的图形关于 y 轴对称;奇 函数的图形 关于原点对 称

若对任意x,x2e(a,b),当xf(x2),则称函 图像表现为 数y=f(x)是区间(a,b)上的单调减少函数,单调增 自左至右是 单 加函数和单调减少函数统称单调函数,若函数 单调上升的 调 y=f(x)是区间(a,b)上的单调函数,则称区间(a,b) 曲线;单调 性 为单调区间 减少的函数 的图像表现 为自左至右 是单调下降 的曲线 如果存在M>0,使对于任意x∈D满足 图像在 有 (x≤M则称函数y=fx)是有界的 直线y=-M 界 与y=M之 性 间 如果存在常数T,使对于任意x∈D,x+T∈D, 在每 周 有fx+T)=f(x)则称函数y=f(x)是周期函数,通 个周期内的 期 常所说的周期函数的周期是指它的最小周期 图像是相同 性 的
6 单 调 性 若 对 任 意 , ( , ) 1 2 x x a b , 当 1 2 x x 时 , 有 ( ) 1 f x ( ) 2 f x ,则称函数 y f (x)是区间(a,b)上的单 调增加函数;当 1 2 x x 时,有 ( ) 1 f x ( ) 2 f x ,则称函 数 y f (x)是区间(a,b)上的单调减少函数,单调增 加函数和单调减少函数统称单调函数,若函数 y f (x)是区间(a,b)上的单调函数,则称区间(a,b) 为单调区间 单 调 增 加的函数的 图像表现为 自左至右是 单调上升的 曲线; 单调 减少的函数 的图像表现 为自左至右 是单调下降 的曲线 有 界 性 如 果 存 在 M 0 , 使 对 于 任 意 x D 满 足 f (x) M 则称函数 y f (x)是有界的 图 像 在 直 线 y M 与 y M 之 间 周 期 性 如果存在常数T ,使对于任意x D,x T D, 有 f (x T) f (x) 则称函数 y f (x)是周期函数,通 常所说的周期函数的周期是指它的最小周期 在 每 一 个周期内的 图像是相同 的
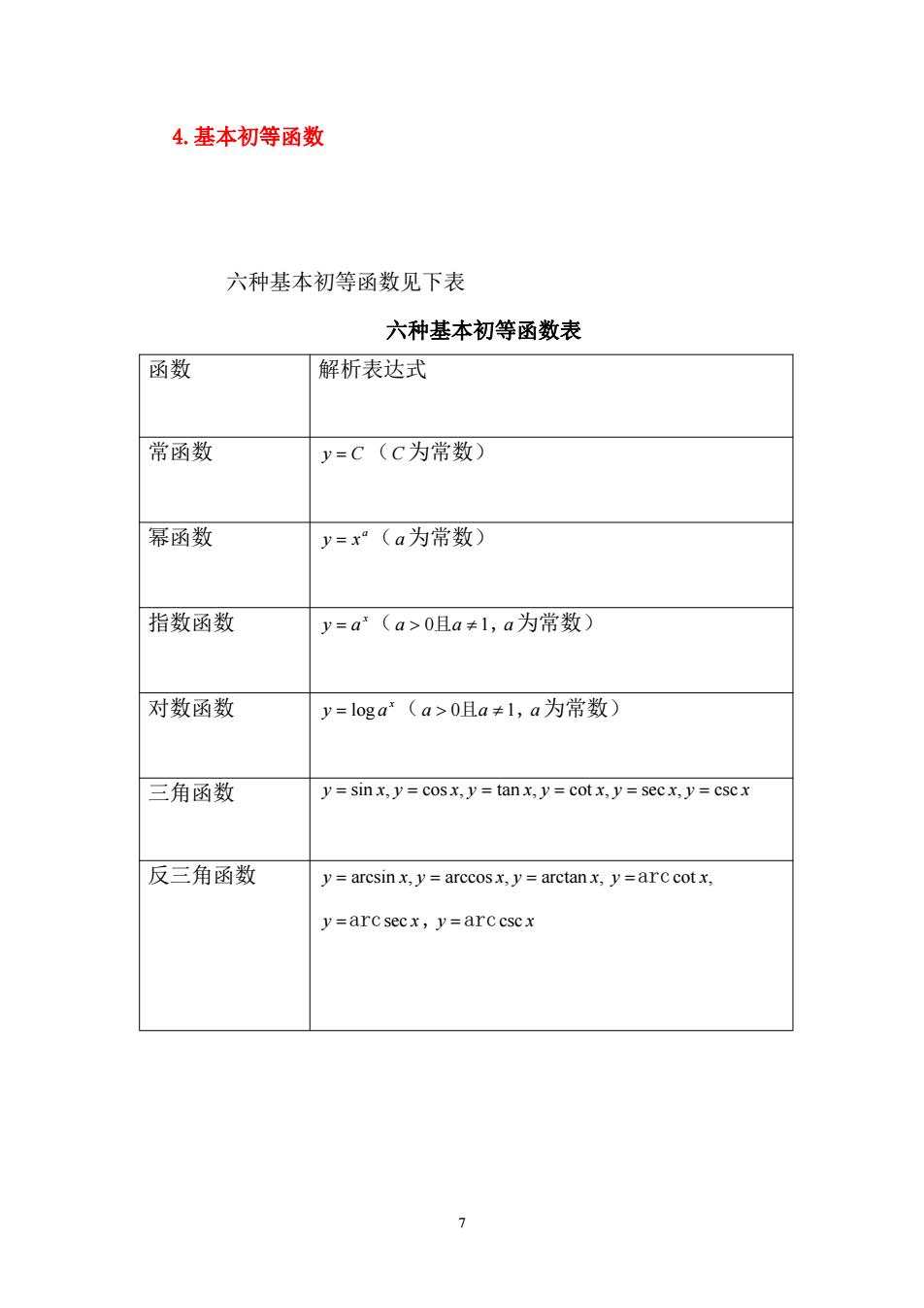
4.基本初等函数 六种基本初等函数见下表 六种基本初等函数表 函数 解析表达式 常函数 y=C(C为常数) 幂函数 y=x(a为常数) 指数函数 y=a(a>0且a≠l,a为常数) 对数函数 y=loga(a>0且a≠l,a为常数) 三角函数 y=sinx,y=cosx,y=tanx,y=cotx,y=secx,y=cscx 反三角函数 y=arcsinx,y=arccosx,y=arctanx,y=arc cotx, y=arcsecx,y=arccscx >
7 4.基本初等函数 六种基本初等函数见下表 六种基本初等函数表 函数 解析表达式 常函数 y C (C 为常数) 幂函数 a y x (a为常数) 指数函数 x y a (a 0且a 1,a为常数) 对数函数 x y log a (a 0且a 1, a为常数) 三角函数 y sin x, y cos x, y tan x, y cot x, y sec x, y csc x 反三角函数 y arcsin x, y arccos x, y arctan x, y arccot x, y arcsec x , y arccsc x

5.反函数、复合函数和初等函数 反函数、复合函数和初等函数的定义见下表 几种函数的定义表 函数种 定义 举例 类 设函数y=f(x)为定义在数集D上 函 数 的函数,其值域为W.如果对于数集W y=sinx 中的每个数y,在数集D中都有惟一确 定的数x使y=fx)成立,则得到一个定 反函数 的反函数为 义在数集W上的以y为自变量,x为因 x=arcsin y 变量的函数,称其为函数y=f(x)的反 (-1≤y≤1) 函数,记为x=y),其定义域为W, 值域为D 复合函 若函数y=f(w)的定义域为D,,函 由函数y=2 数 数u=p(x)在D,上有定义,其值域为 和u=cosx复合而
8 5. 反函数、复合函数和初等函数 反函数、复合函数和初等函数的定义见下表 几种函数的定义表 函数种 类 定 义 举 例 反函数 设函数 y f (x) 为定义在数集 D 上 的函数,其值域为W .如果对于数集W 中的每个数 y ,在数集D中都有惟一确 定的数 x使 y f (x)成立,则得到一个定 义在数集W 上的以 y 为自变量, x 为因 变量的函数,称其为函数 y f (x) 的反 函数,记为 ( ) 1 x f y ,其定义域为W , 值域为D 函 数 y sin x ) 2 π 2 π ( x 的反函数为 x arcsin y (1 y 1) 复合函 数 若函数 y f (u)的定义域为D1 ,函 数u (x) 在 D2 上有定义 ,其值域为 由函数 2 y u 和 u cos x 复合而

W2={uu=p(x),x∈D}且W,cD,则对于 成的复合函数为 任 y=(cosx)2. 一x∈D2,通过函数u=p(x)有确定的 由 函 数 u∈W与之对应,通过函数y=fw有确 y=1-u 和 定的y值与之对应.这样对于任一 u=2+e不能复合 x∈D,通过函数u有确定的y值与之对 成复合函数 应,从而得到一个以x为自变量,y为 因变量的函数,称其为由函数y=f 和u=p(x)复合而成的复合函数,记为 y=fo(x】,其定义域为D,u称为中 间变量 由基本初等函数经过有限次四则 初等函 运算和有限次复合运算而得到的,且用 f(x)=2+5(In x) 数 一个式子表示的函数,称为初等函数 二、主要解题方法 1.求函数定义域的方法 例1求下列函数的定义域: (1)y=v16-x2+Insinx 9
9 { ( ), } 2 D2 W u u x x 且W2 D1,则对于 任 一 D2 x ,通过函数 u (x) 有确定的 W2 u 与之对应,通过函数 y f (u)有确 定的 y 值与之对应.这样对于任一 D2 x ,通过函数u 有确定的 y 值与之对 应,从而得到一个以 x 为自变量, y 为 因变量的函数,称其为由函数 y f (u) 和u (x)复合而成的复合函数,记为 y f [(x)],其定义域为 D2 ,u 称为中 间变量 成的复合函数为 2 y (cos x) . 由 函 数 y 1 u 和 x u 2 e 不能复合 成复合函数 初等函 数 由基本初等函数经过有限次四则 运算和有限次复合运算而得到的,且用 一个式子表示的函数,称为初等函数 1 4 ( ) 2 5(ln ) 2 f x x x 二、主要解题方法 1.求函数定义域的方法 例 1 求下列函数的定义域: (1) y = 2 16 x +ln sin x

(2)y=- +arcsin(1). 1 解(1)由所给函数知,要使函数y有定义,必须满足两种情况, 偶次根式的被开方式大于等于零或对数函数符号内的式子为正,可建 立不等式组,并求出联立不等式组的解.即 16-x2≥0, 推得 -4≤x≤4 sinx>0, 2m0, 推得 -V5<x<5, 0≤x≤4, 即0≤x<√3, 因此,所给函数的定义域为 [0,V3). 小结函数由解析式给出时,其定义域是使解析式子有意义的一切 函数.为此求函数的定义域时应遵守以下原则: (①)在式子中分母不能为零: (II)在偶次根式内非负: 10
10 (2) y = 1) 2 arcsin( 3 1 2 x x . 解 (1) 由所给函数知,要使函数 y 有定义,必须满足两种情况, 偶次根式的被开方式大于等于零或对数函数符号内的式子为正,可建 立不等式组,并求出联立不等式组的解.即 sin 0, 16 0, 2 x x 推得 2 π (2 1)π 0, 1, 2 4 4 n x n n x 这两个不等式的公共解为 4 x π 与0 x π 所以函数的定义域为[4, π) (0, π) . (2) 由所给函数知,要使函数有定义,必须分母不为零且偶次根 式的被开方式非负;反正弦函数符号内的式子绝对值小于等于 1.可 建立不等式组,并求出联立不等式组的解.即 1 1 , 2 3 0 , 3 0 , 2 x x x 推得 0 4 , 3 3 , x x 即 0 x 3 , 因此,所给函数的定义域为 [0, 3) . 小结 函数由解析式给出时,其定义域是使解析式子有意义的一切 函数.为此求函数的定义域时应遵守以下原则: (I) 在式子中分母不能为零; (II)在偶次根式内非负;