Calculus Exercise Chapter 1 Function 1.Are they functions in the following graphs? rz☑ 4p→. 2.Are they functions in the following tables? d x111 x123 x111 )i23 111 x)11I e x123 x223 x123 x)456 x)111 )121o2
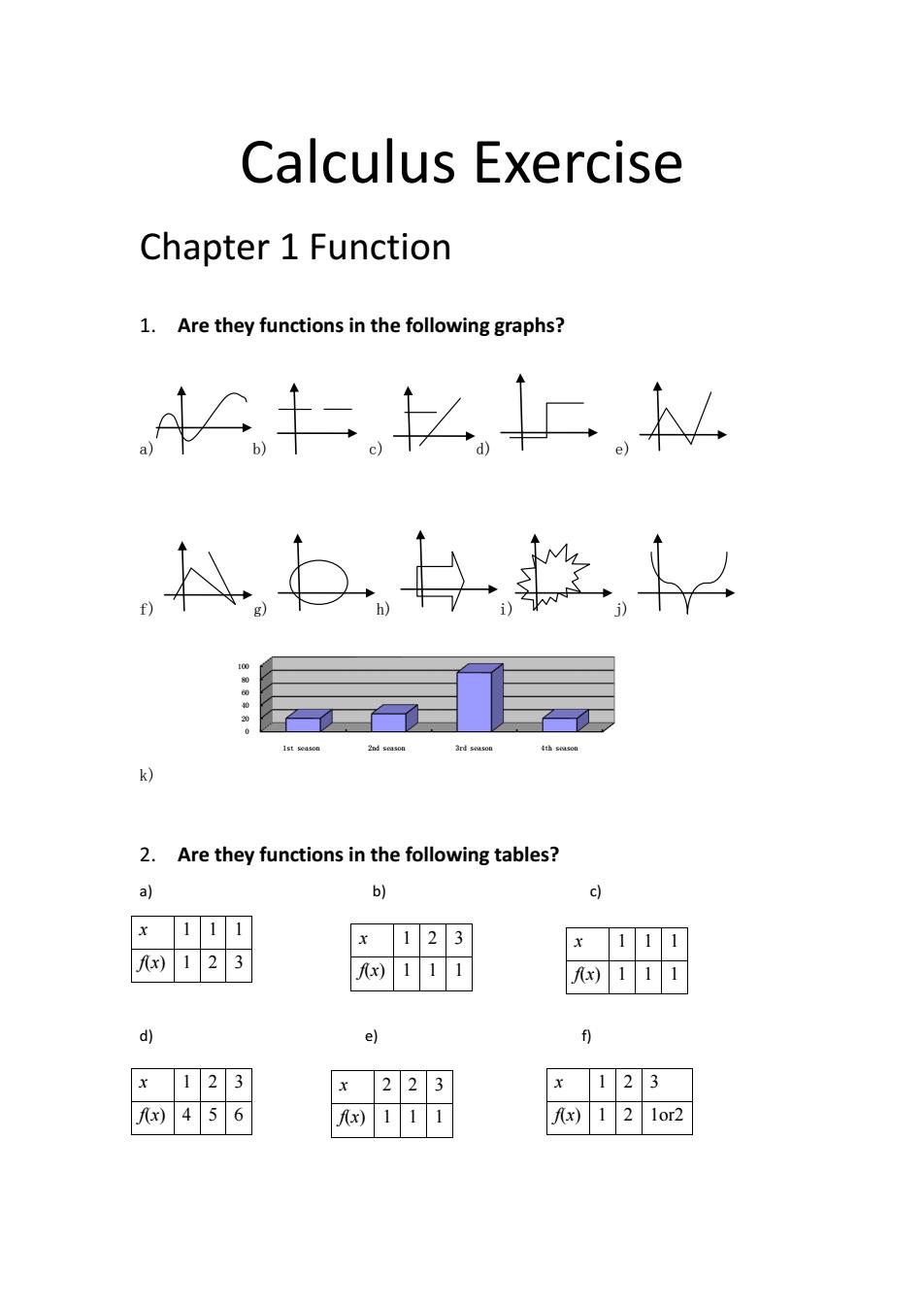
Calculus Exercise Chapter 1 Function 1. Are they functions in the following graphs? a) b) c) d) e) f) g) h) i) j) k) 2. Are they functions in the following tables? a) b) c) d) e) f) 0 20 40 60 80 100 1st season 2nd season 3rd season 4th season x 1 1 1 f(x) 1 2 3 x 1 2 3 f(x) 1 1 1 x 1 1 1 f(x) 1 1 1 x 1 2 3 f(x) 4 5 6 x 2 2 3 f(x) 1 1 1 x 1 2 3 f(x) 1 2 1or2

3.Are they functions in the following formulas? a)f(x)=sinx;b)f(x)=0. of()=f xo -x,otherwise; d f()=2 Ux=1 -2,fx=-l e)f(x)=y,where y satisfiesx2+y2=1; 「sinx,ifx0. h)f(x)=cosl; i)fx)=g2(x),where g(x)=tanx,in(-π/2,π/2: Dr++4-2in0+啡为=sire)in(m以 sin(e*) 3.ifx1. sr=me sine*-vx2+3x+I,ifx2+3x+1z0 =F不,刂-高-@gw wf)=log(sinx-ly为fx)=--可+1 4 y)f(x)=1+x+++x,where N is a positive integer; z)f(x)=1+sinx+sin 2x+..+sin Nx,where N is a positive integer; 4.Are they functions in the following sentences? a)f(n)denotes the average temperature in degree of the days since 01/12/2013; b)f(n)is denoted as the number of the students of the class n;
3. Are they functions in the following formulas? a) f x x ( ) sin ; b) f x( ) 0; c) , 0, ( ) , ; x if x f x x otherwise d) 2, 1, ( ) 2, 1; if x f x if x e) 2 2 f x y y x y ( ) , where satisfies 1; f) 1/ ( ) , (0, ); x f x e x g) sin , 0, ( ) 1, 0, , 0; x if x f x if x x if x h) 2, 0, ( ) 0, 0; if x f x if x h) f x( ) cos1; i) 2 f x g x g x x ( ) ( ), where ( ) tan , in ( / 2, / 2); j) 2 sin( ) ( ) , in (0, ); 4 2 x e f x x x k) 2 cos ( ) sin( ), in ( , ); x x e f x e l) 3, if 0, ( ) sin( ( )), where ( ) ; 3, if 0 x f x h x h x x m) f x e ( ) ; n) 1, if 1, ( ) 2, if 2; x f x x o) 2 2 1, if 1, ( ) 2, if 1, x f x x p) 1, if 1, ( ) 2, if 2; x f x x q) log cos , if cos 0, ( ) 1 cos , if cos 0; x x f x x x r) 2 2 2 2 sin 3 1, if 3 1 0, ( ) 1 log | | , if 3 1 0; 1 x e x x x x f x x x x x s) 2 f x x ( ) 1; t) 1 ( ) cos f x x u) f x x ( ) loglog ; v) f x x x ( ) sin w) f x x ( ) log(sin 1); x) 4 3 2 1 4 ( ) 1 ; 1 3 2 1 f x x x x x y) 2 ( ) 1 ... ,where is a positive integer; N f x x x x N z) f x x x Nx N ( ) 1 sin sin 2 ... sin ,where is a positive in teger; 4. Are they functions in the following sentences? a) f(n) denotes the average temperature in degree of the days since 01/12/2013; b) f(n) is denoted as the number of the students of the class n;

c)f(n)is denoted as the number of the students under 17 ages of the class n. d)f(n)is denoted as the number of positive results in n tests; gaBaaieashgpoIyPceoheoCkaaheomoommaTteB g)f(n)is denoted as the expected number of the good medals of the country n in the next Olympic Games. 5.Find the domains of the following functions: a)f(x)=0.b)f(x)=sinx;c)f(x)=2x2-x+3 d)f(x)=e+c0. )(log(1): 1 0-2-+2nf国=(可w2-- 1 f(x)=sin(log(x));m)f(x)=log(cosx)n)f(x)=-e' o=-cs/-画,g倒=e阿 r)f(x)=Vx2-3x+1:s)f(x)= =, V Ixl -1,ifx-l, cosx,if-31 v)f(x)=log(g(x)),where g(x)=0,if x=1. -1,ifx<l x123 x)321 6.Find the ranges of the following functions: a)fx)=上b)fx)=sinx3;dfx)=xe2;d)fx)=em
c) f(n) is denoted as the number of the students under 17 ages of the class n. d) f(n) is denoted as the number of positive results in n tests ; e) f(n) is denoted as the highest velocity of the car in type n; f) f(n) is denoted as the possibility price of the stock n in the tomorrow market; g) f(n) is denoted as the expected number of the good medals of the country n in the next Olympic Games. 5. Find the domains of the following functions: a) f x( ) 0; b) f x x ( ) sin ; c) 2 f x x x ( ) 2 3; d) 2 cos ( ) ; x x f x e e) 2 f x x ( ) log 1 ; f) 2 1 ( ) ; 3 1 f x x x g) 1 ( ) ; 1 x f x x h) 1 f x( ) ; x i) 2 1 ( ) ; 3 2 f x x x j) f x x x ( ) sin 1 ; k) 3 1 ( ) 3 ; 2 1 f x x x l) f x x ( ) sin log( ) ; m) f x x ( ) log(cos ) n) ( ) 1 ; x f x e o) 1 ( ) ; 1 cos f x x p) f x x ( ) tan ; q) 2 1 ( ) ; x f x e r) 2 f x x x ( ) 3 1; s) | 1| ( ) ; | | x f x x t) 2 2 1, if 2, ( ) 1, if 1; x f x x u) sin , if 1 2, ( ) cos , if -3< 0; x x f x x x v) 1, if 1, ( ) , otherwise; x x f x x w) ( ) , if sin 1; x f x e x x) , if 2 1 0, ( ) log , otherwise; x e x f x x y) 1, 1, ( ) log , where ( ) 0, 1, 1, 1. if x f x g x g x if x if x z) 6. Find the ranges of the following functions: a) f x( ) 1; b) 3 f x x ( ) sin ; c) 2 ( ) ; x f x xe d) 2 1 ( ) ; x f x e x 1 2 3 f(x) 3 2 1

=骨点N=F i)f(x)=xx2-1;i)f(x)=/cosx;k)f(x)=log(x+1);1)f(x)=tan 1f=闭=7o))=m2x+ s)f(x)=sece";t)f(x)=e;u)f(x)=logsinx+v)f(x)=e 1,ifx>0, w)f(x)=0,ifx=0,x)f(x)= +2x-1,ix2l0f)= x2+1,ifx=1, -1,ifx<0; e",otherwise; cosx,otherwise. x123 )321 7.Find the domains and ranges of the following functions by graph: b) 8.Indicate if the following functions are invertible or invertible after restrict the domains,if so find their inverse functions and their restricted domains if any: a)f(x)=0,b)f(x)=x,c)f(x)=x;d)f(x)=x+1;e)f(x)=2x-3, f)f(x)=/x+I;g)f(x)=x2-1;h)f(x)=x+x+1;i)f(x)=x;
e) sin ( ) ;x f x e f) 1 ( ) ; 1 x f x x g) 1 1 ( ) ; x x f x e h) 2 f x x ( ) 2; i) 2 f x x x ( ) 1; j) f x x ( ) cos ; k) f x x ( ) log( 1); l) f x x ( ) tan ; m) sin ( ) ; 1 x x f x e n) 1 ( ) ; 1 x x e f x e o) 2 f x x ( ) sin 1; p) 2 1 ( ) ; 1 f x x q) 1 ( ) ; cos 1 f x x r) 2 3 f x x x ( ) sin sin ; s) ( ) sec ; x f x e t) 2 cos ( ) ; x f x e u) f x x ( ) logsin 1; v) log ( ) ; x f x e w) 1, if 0, ( ) 0, if 0, 1, if 0; x f x x x x) 3 2 1, if 1, ( ) , otherwise; x x x x f x e y) 2 1, if 1, ( ) cos , otherwise. x x f x x z) 7. Find the domains and ranges of the following functions by graph: a) b) 1 0 1 8. Indicate if the following functions are invertible or invertible after restrict the domains, if so find their inverse functions and their restricted domains if any: a) f x( ) 0; b) f x x ( ) ; c) 3 f x x ( ) ; d) f x x ( ) 1; e) f x x ( ) 2 3; f) f x x ( ) 1; g) 2 f x x ( ) 1; h) 2 f x x x ( ) 1; i) 2 f x x ( ) 1 ; x 1 2 3 f(x) 3 2 1 1 0 1

)fx)=e+上kf(x)= F-3x+20f)=e:mf)=e2-+2 1 n)f(x)=e+2e*+l;o)f(x)=sine'-1;q)f(x)=esinx-; x,ifx≥0, f(x)x-1川+l)f(x)= 2,ix<0wf)=m≥0 -1,if x<0. sinx,ifx≥0, 1,if x21, x刘f(x)= tans.ifx<()if -l,ifx≤-l. x123 )456 9.Draw the inverse functions of the following functions from their graphs: 10.Value of the following functions: a)f(x)=sinx,thenf(0)= b)f(x)=2x2-1;thenf①= c)f(x)=cosx+e;thenf(z/2)=d)f(x)=x2-logx,thenf(1)= 。f)- ;thenf(π)= f)f(x)=xx+2;thenf(2)= g)f(x)=ve*+1;thenf(0)= h)f(x)=log(x2)thenf(ve)= i)f(1)=2,g(2)=3,theng(f(1))= k)f⑩=2,g(2)=2,theng(g(2)=
j) ( ) 1; x f x e k) 2 1 ( ) ; 3 2 f x x x l) 1 ( ) ; x f x e m) 2 1 ( ) 2; x f x e n) 2 ( ) 2 1; x x f x e e o) 3 ( ) sin 1; x f x e q) sin 1 ( ) ; x f x e r) ( ) log(1 cos ); x f x e s) 1 ( ) ; 1 x x e f x e t) f x x ( ) loglog( 1); u) f x x ( ) | 1| 1; v) 3 , if 0, ( ) , if 0. x x f x x x w) 1, if 0, ( ) 1, if 0. x f x x x) sin , if 0, ( ) tan , if 0. x x f x x x y) 1, if 1, ( ) , if -1< 1, 1, if 1. x f x x x x z) 9. Draw the inverse functions of the following functions from their graphs: a) b) 1 0 1 10. Value of the following functions: a) f x x f ( ) sin ; then (0) b) 2 f x x f ( ) 2 1; then (1) c) ( ) cos ; then ( / 2) x f x x e f d) 2 f x x x f ( ) log ; then (1) e) sin ( ) ; then ( ) 1 x f x f x f) f x x x f ( ) 2; then (2) g) ( ) 1; then (0) x f x e f h) 2 f x x f e ( ) log( ); then ( ) i) f g f (1) 2, g(2) 3, then ( (1)) k) f g g (1) 2, g(2) 2, then ( (2)) x 1 2 3 f(x) 4 5 6 1 0 1

11.Answer the following questions: a)Iff(x)is invertible,is f(x)+a invertible,where ais any constant? b)If f(x)and g(x)are invertible,is f(x)+g(x)invertible? c)Are the following functions defined in tables even or odd functions? x-101 x-10.51 x-101 )121 gx)202 h)30-3 d)If f(g(x))=g(f(x))=x what the relationship of f(x)and g(x)? e)ffg(x》=gfx》=fx),what is g(x)? f)Is f(g(x))=g(f(x))correct? g)If f(x).g(x)are invertible,is f(g(x))=gf(x))correct? h)If f(2)=3.g(3)=2,is f(g(3))=g(f(3))correct? i)If f(2)=3,g(3)=2,are f(g(3))=3,g(f(2))=2 correct? )Function is defined.is the domain of this function is -1,x<0 (-,+0)2 k)Does the range of above function equal to [-1,+1]? (is defined.Is the domain of this function is 1)Function f(x)h(x). (-0,+o)2 m)Does the domain of above function equal to DDwhere D,denotes the domain of f(x)? n)Does the range of above function equal toR,where R denotes the range of f(x)?
11. Answer the following questions: a) If f x( ) is invertible,is f x a ( ) invertible, where a is any constant? b) If f x( ) and g x( ) are invertible,is f x g x ( ) ( ) invertible? c) Are the following functions defined in tables even or odd functions? d) If f g x g f x x ( ( )) ( ( )) what the relationship of f x( ) and g x( ) ? e) If f g x g f x f x ( ( )) ( ( )) ( ) , what is g x( ) ? f) Is f g x g f x ( ( )) ( ( )) correct? g) If f x g x ( ), ( ) are invertible, is 1 1 f g x g f x ( ( )) ( ( )) correct? h) If f g (2) 3, (3) 2 , is f g g f ( (3)) ( (3)) correct? i) If f g (2) 3, (3) 2 , are f g g f ( (3)) 3, ( (2)) 2 correct? j) Function 1, 0, ( ) 1, 0 x f x x is defined. Is the domain of this function is ( , )? k) Does the range of above function equal to [-1,+1]? l) Function ( ), 0, ( ) ( ), 0 g x x f x h x x is defined. Is the domain of this function is ( , )? m) Does the domain of above function equal to D D g h ,where Df denotes the domain of f x( ) ? n) Does the range of above function equal to R R g h ,where Rf denotes the range of f x( ) ? x -1 0 1 f(x) 1 2 1 x -1 0.5 1 g(x) 2 0 2 x -1 0 1 h(x) 3 0 -3

o)sf)=18)>0, defined a function? -l,g(x)≤0 p)What is the domain of above function? m)If f(2)=3.f(3)=2,what is the value of f(f'(3))? n)f(x)is a positive function,can we say it is increasing function? o)f(x)is a piecewise defined function,which is defined in two interval A and B Can we say AnB is empty? p)f(x)is a piecewise defined function,which is defined in two interval A and B. Can we say UB=(-0,+0)? u)f(x)and g(x)are two piecewise defined functions,which defined in different intervals.Isf(x)+g(x)still a function,if so,what is its domain? v)f(x)and g(x)are two piecewise defined functions,which defined in different intervals.Isf(g(x))still a function,if so,what is its domain? wo-女 If g(x)and h(x)are both one-to-one,is f(x) invertible?? x)f(x)is invertible,is f(x)invertible? y)f(x)and g(x)have the same domains,can we say that they have the same ranges? z)f(x)and g(x)have the same ranges,can we say that they have the same domains? 12.Fill in the following blanks a)If f(x)is an odd function,than f(0)=_ b)If f(x)is an odd function,than f(x)*f(-x)=_ c)If f(x)is an odd function,than for x0,f(x)/f(-x)=_
o) Is 1, ( ) 0, ( ) 1, ( ) 0 g x f x g x defined a function? p) What is the domain of above function? m) If f f (2) 3, '(3) 2 , what is the value of f f ( '(3)) ? n) f x( ) is a positive function, can we say it is increasing function? o) f x( ) is a piecewise defined function, which is defined in two interval A and B. Can we say A B is empty? p) f x( ) is a piecewise defined function, which is defined in two interval A and B. Can we say A B ( , ) ? u) f x( ) and g x( ) are two piecewise defined functions, which defined in different intervals. Is f x g x ( ) ( ) still a function, if so, what is its domain? v) f x( ) and g x( ) are two piecewise defined functions, which defined in different intervals. Is f g x ( ( )) still a function, if so, what is its domain? w) ( ), if , ( ) ( ), if . g x x A f x h x x B If g x( ) and h x( ) are both one-to-one, is f x( ) invertible? x) f x( ) is invertible, is f x( ) invertible? y) f x( ) and g x( ) have the same domains, can we say that they have the same ranges? z) f x( ) and g x( ) have the same ranges, can we say that they have the same domains? 12. Fill in the following blanks a) If f x( ) is an odd function, than f (0) ____. b) If f x( ) is an odd function, than f x f x ( )* ( ) ____. c) If f x( ) is an odd function, than for x f x f x 0, ( ) / ( ) ____

d)If f(x)is an odd function,than for(x)+f (-x)=_ e)If f(x)is an odd function,then f()=_ f)If f(x)is an even function,than f(x)f(-x)= g)If f(x)is an even function,than for f(x)0,f(x)/f(-x)=_ h)If f(x)is an even function,than for (x)-f(-x)= [g(x).ifx>0. i)If f(x)=0,ifx=0,is an odd function,than g(x)(x). (h(x),ifx(b)implies a_b. n)If f(x)is an decreasing function,than f(a)>f(b)implies a_b. o)ff0=2g2)=3,then0+82 f0)g(2) p)If f(1)=2.g(2)=3,then g(f(1))= q)Iff(3)=2,g(2)=3.f(2)=1g(1)=0,then f(g(x))*g(f(x))2=_ r)Fill the blank in the following tables: x 12 3 x 123 Ax) 3 2 1 fx) 021 g(x) 45 6 g(x) 1 20 Ax)+2 g(x) fx)"g(x) 1 2 3 123 0 2 1 Ax) 32 1 g(x) 1 2 0 g(x) 0 g(x)/fx) gx)》
d) If f x( ) is an odd function, than for 3 3 f x f x ( ) ( ) ____. e) If f x( ) is an odd function, then f (0) __________. f) If f x( ) is an even function, than f x f x ( )* ( ) ____. g) If f x( ) is an even function, than for f x f x f x ( ) 0, ( ) / ( ) ____. h) If f x( ) is an even function, than for 3 3 f x f x ( ) ( ) ____ i) If ( ), if 0, ( ) 0, if 0, ( ), if 0. g x x f x x h x x is an odd function, than g x( ) ____ h x( ) . j) If f x( ) is defined as above, but it is an even function, than g x( ) ____ h x( ) . k) If the domain of f x( ) is A, then the domain of sin( ( )) f x is ______. l) If the range of f x( ) is [-1,1], then the range of exp( ( )) f x is ______. m) If f x( ) is an increasing function, than f a f b ( ) ( ) implies a ___ b. n) If f x( ) is an decreasing function, than f a f b ( ) ( ) implies a ___ b. o) If 2 (1) (2) (1) 2, g(2) 3, then (1) (2) f g f f g ___________. p) If f g f (1) 2, g(2) 3, then ( (1)) ____________. q) If 2 (3) 2, g(2) 3, (2) 1, g(1) 0, then ( ( )) ( ( )) x f f f g x g f x ______. r) Fill the blank in the following tables: x 1 2 3 f(x) 3 2 1 g(x) 4 5 6 f(x)+2 g(x) x 1 2 3 f(x) 0 2 1 g(x) 1 2 0 f(x)* g(x) x 1 2 3 f(x) 0 2 1 g(x) 1 2 0 g(x)/ f(x) x 1 2 3 f(x) 3 2 1 g(x) 2 0 3 f( g(x))

s)Let f(x)be a invertible function,and f(a)=b,thenf(b)=_ t)Let f(x)be increasing function in (+)a>b,then f(a)_f(b) u)Let f(x)be increasing function in (+)a>b,then f(a)f(b) v)Let f(x)and g(x)be both increasing functions in (,+o),a>b,then f(a)+8(a)_ _f(b)+g(b) w)Let f(x)and g(x)be increasing and decreasing functions respectively in (-o,+0),a>b,then f(a)-g(a) fb)-gb) x)Let f(x)and g(x)be both increasing functions in (,+)a>b,then f(a)*g(a)—fb)*gb). y)Let f(x)and g(x)be both increasing functions in (,+o),a>b,then f(a)+g(a) f(b)+g(b). z)Let f(x)and g(x)be increasing and decreasing functions respectively in (-,+o),a>b,then for g(a,g(b)≠0,f(a/g(ad_ (b)1gb)
s) Let f x( ) be a invertible function, and f a b ( ) , then 1 f b( ) _________. t) Let f x( ) be increasing function in ( , ) , a b , then f a( ) ____ f b( ) . u) Let f x( ) be increasing function in ( , ) , a b , then 1 f a( ) __ 1 f b( ) . v) Let f x( ) and g x( ) be both increasing functions in ( , ) , a b , then f a g a ( ) ( ) __________ f b g b ( ) ( ) . w) Let f x( ) and g x( ) be increasing and decreasing functions respectively in ( , ) , a b , then f a g a ( ) ( ) __________ f b g b ( ) ( ) . x) Let f x( ) and g x( ) be both increasing functions in ( , ) , a b , then f a g a ( )* ( ) __________ f b g b ( )* ( ) . y) Let f x( ) and g x( ) be both increasing functions in ( , ) , a b , then f a g a ( ) ( ) __________ f b g b ( ) ( ) . z) Let f x( ) and g x( ) be increasing and decreasing functions respectively in ( , ) , a b , then for g a g b f a g a ( ), ( ) 0, ( )/ ( ) __________ f b g b ( )/ ( )

Chapter 2 Limit 1.Fill in the blanks a)If limf(x)=0,then lim f(x)= b)If lim /()=lim f(x)=2,then lim f(x)= 日f吗+=L,hen四U+-》= h f▣0+f0=100,em(0-fN-)= h e)If lim f(x)g(x)=2.lim g(x)=5,then lim f(x)= If lim /()g()=0.limg(x)=2,then lim f(x)= g)If lim f(x)/g(x)=0,limg(x)=1,then lim f(x)=_ hfm四.l,heng= i)If lim f(x)=2,then lim(-f(x))=_ 1 )fmf=3,theni9— k)If lim f(x)=c,then lim[af(x)(x)= )fmf=3,henm广西= m)If limx'f(x)=1,then limf(x)=_ n)If f(x)=-f(-x),limf(x)=L,then L= o)If lim f(x)=2.limf(x)=3.,then lim f(f(x))=_ p)If limf(x)=3.limg(x)=2.then lim(f(x)+2g(x))= a)If limf(x)=3.limg(x)=2.then lim (3f(x)-g(x))=_
Chapter 2 Limit 1. Fill in the blanks a) If 0 lim ( ) 0 x x f x , then 0 lim ( ) x x f x ______ b) If 0 0 lim ( ) lim ( ) 2 x x x x f x f x , then 0 lim ( ) x x f x ______ c) If 0 0 0 ( ) ( ) lim h f x h f x L h , then 0 0 0 lim ( ) ( ) h f x h f x ______ d) If 0 (1 ) (1) lim 1000 h f h f h , then 0 lim (1) (1 ) h f f h _____ e) If 0 0 lim ( ) ( ) 2, lim ( ) 5, x x x x f x g x g x then 0 lim ( ) x x f x ______ f) If 0 0 lim ( ) ( ) 0, lim ( ) 2, x x x x f x g x g x then 0 lim ( ) x x f x ______ g) If 0 0 lim ( ) / ( ) 0, lim ( ) 1, x x x x f x g x g x then 0 lim ( ) x x f x ______ h) If 0 ( ) lim 1, x f x x , then 0 lim ( ) x f x ______ i) If 0 lim ( ) 2 x x f x , then 0 lim ( ) x x f x ______ j) If 0 lim ( ) 3 x x f x , then 0 1 lim x x f x( ) ______ k) If 0 lim ( ) x x f x c , then 0 2 lim ( ) ( ) x x af x bf x ______ l) If 0 lim ( ) 3 x x f x , then 0 lim ( ) x x f x ______ m) If 2 0 lim ( ) 1, x x f x then 0 lim ( ) x f x ______ n) If 0 ( ) ( ), lim ( ) , x f x f x f x L then L= o) If 1 2 lim ( ) 2,lim ( ) 3, x x f x f x , then 1 lim ( ( )) x f f x ______ p) If 0 0 lim ( ) 3, lim ( ) 2, x x f x g x then 0 lim ( ) 2 ( ) x f x g x _____ q) If 0 0 lim ( ) 3, lim ( ) 2, x x f x g x then 2 0 lim 3 ( ) ( ) x f x g x ____