
第四部分图论 图是最直观的模型
第四部分 图论 图是最直观的模型
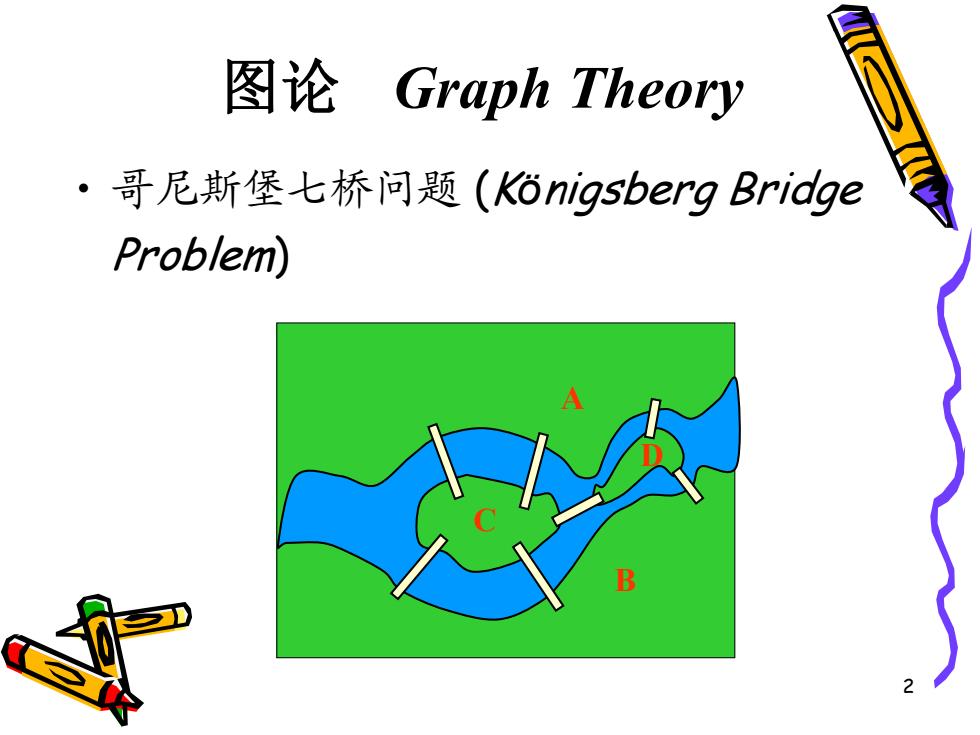
图论 Graph Theory ·哥尼斯堡七桥问题(k6 nigsberg Bridge Problem)
2 图论 Graph Theory • 哥尼斯堡七桥问题 (Königsberg Bridge Problem) B A C D

瑞士数学家礼eonhard Euler(1707-178 在1736年发表第一篇图论方面的论文,讨 论了哥尼斯堡七桥问题,奠基了图论中的 一些基本定理。 OB
3 •瑞士数学家Leonhard Euler (1707-1783) 在1736年发表第一篇图论方面的论文,讨 论了哥尼斯堡七桥问题,奠基了图论中的 一些基本定理。 A B C D

第十四章图的基本概念
第十四章 图的基本概念
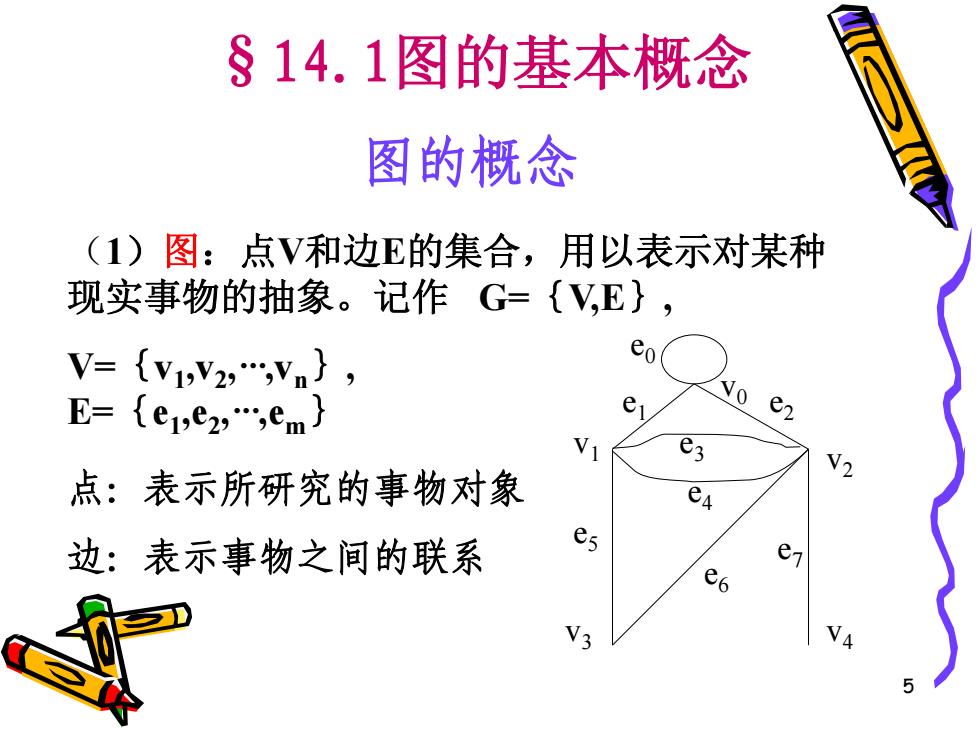
§14.1图的基本概念 图的概念 (1)图:点V和边E的集合,用以表示对某种 现实事物的抽象。记作G={V,E} V={vpV2",Vn}, E={e1e2,em】 e 0 e e3 点:表示所研究的事物对象 e4 边:表示事物之间的联系 es e6 V3
5 §14.1图的基本概念 图的概念 (1)图:点V和边E的集合,用以表示对某种 现实事物的抽象。记作 G={V,E}, V={v1 ,v2 ,···,vn}, E={e1 ,e2 ,···,em} 点:表示所研究的事物对象 边:表示事物之间的联系 v1 v2 v3 v4 v0 e1 e2 e3 e4 e5 e6 e7 e0

有向图— 题e,)有方向y为始点,Y为终个 图 此时(v,V)≠(vV) 无向图一边e=(,v,)无方向,此时(v,)=(v e6 e e 有向图 e e e e 4 向图 es es V4)V4’V3) e4(V3,V4)=(V4,V3) e5=(V3,V4)=(V43 有向图各边改为无向边后的无向图称为原来图的基图
6 有向图 无向图 ——边e=(vi, vj)有方向vi为始点,vj为终点 ——边e=(vi, vj)无方向,此时 (vi, vj)=(vj,vi) e e4=(v3,v4)=(v 4, v3) 4=(v3,v4)≠(v4,v3) e5=(v3,v4)=(v 4, v3) 此时(vi, vj)≠(vj,vi) 1 v 2 v 3 v 4 v e1 2 e e3 e4 5 e 6 e 1 v 2 v 3 v 4 v e1 2 e e3 e4 5 e 6 e e5=(v4,v3)≠(v3,v4 ) 图 有 向 图 无 向 图 有向图各边改为无向边后的无向图称为原来图的基图

常用名词 1、端点和关联边: 若ek={y,y,}∈E,则称点y,是边e的端点, ② 点y和v的关联边 2、相邻点和相邻边: 一条边的两个端点称湘邻点,简称邻点, 端点落在同一个顶点的称为相邻边,简称皴 3、多重边与环: e, 具有相同端点的边称寿重边或平行边 两个端点落在同一个痕的边称为环。 e, e6 4、多重图和简单图: V20 ey 含有多重边的图称为多重图; 无环也无多重边的图称为简单图
7 常用名词 1 v 2 v 3 v 4 v e1 2 e e3 e4 5 e 6 e 1、端点和关联边: 点 和 的关联边 若 则称点 、 是 边 的端点,边 是 i j k i j i j k k v v e {v ,v }E, v v e e 2、相邻点和相邻边: 端点落在同一个顶点的边称为相邻边,简称邻边 一条边的两个端点称为相邻点,简称邻点, 3、多重边与环: 两个端点落在同一个顶点的边称为环。 具有相同端点的边称为多重边或平行边; 4、多重图和简单图: 无环也无多重边的图称为简单图。 含有多重边的图称为多重图;

通常用G表示无向图,D表示有向图,也常用G泛揖 无向图和有向图,用e表示无向边或有向边. (G),E(G),V(D),E(D):G和D的顶点集,边集 n阶图:n个顶点的图 有限图:V,E都是有穷集合的图 零图:E=0 平凡图:1阶零图 空图:V=0,空图记为⑦ 8
8 通常用G表示无向图, D表示有向图, 也常用G泛指 无向图和有向图, 用ek表示无向边或有向边. V(G), E(G), V(D), E(D): G和D的顶点集, 边集. n 阶图: n个顶点的图 有限图: V, E都是有穷集合的图 零图: E= 平凡图: 1 阶零图 空图: V= ,空图记为

邻域和关联集 设无向图G,v∈V(G) v的邻域N(y)={ulu∈V(G)A(w,)∈E(G)Au≠ v的闭邻域N()=N(y)U{} v的关联集I(v)={ele∈E(G)Ae与v关联} 设有向图D,v∈V(D) v的后继元集T(vF{u∈/(D)A∈E(G)Au≠y v的先驱元集TD(y厂{uu∈VD)A∈E(GAu≠ v的邻域No()=T(y)UTD(v) 的闭邻域No()=No(y)U{以
9 邻域和关联集 N(v) (v) D N (v) N (v) {v} D D (v) D N (v) (v) (v) D D D 设无向图G, vV(G) v的邻域 N(v)={u|uV(G)(u,v)E(G)uv} v的闭邻域 = N(v)∪{v} v的关联集 I(v)={e|eE(G)e与v关联} 设有向图D, vV(D) v的后继元集 ={u|uV(D)E(G)uv} v的先驱元集 ={u|uV(D)E(G)uv} v的邻域 v的闭邻域
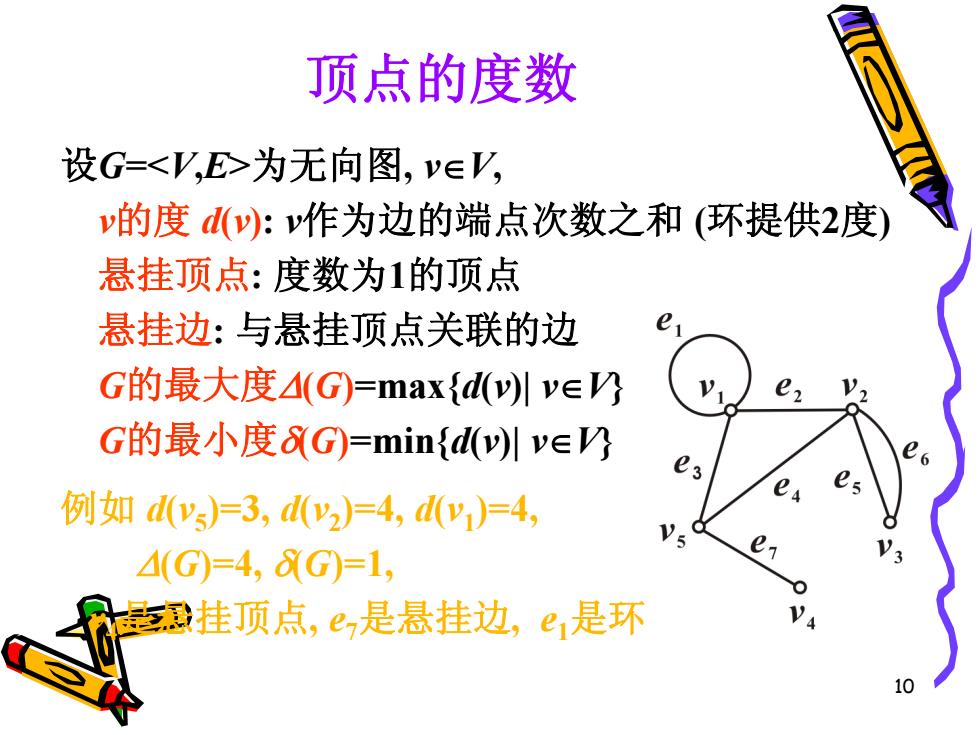
顶点的度数 设G=为无向图,v∈V, v的度d(v吵:作为边的端点次数之和(环提供2度) 悬挂顶点:度数为1的顶点 悬挂边:与悬挂顶点关联的边 G的最大度(G)=max{d(川v∈ e, V2 G的最小度&G)=min{d()川v∈ e e es 例如d(ys)=3,dy2)=4,y)=4, (G)=4,8G)=1, e 挂顶点,e,是悬挂边,e1是环 4 10
10 顶点的度数 设G=为无向图, vV, v的度 d(v): v作为边的端点次数之和 (环提供2度) 悬挂顶点: 度数为1的顶点 悬挂边: 与悬挂顶点关联的边 G的最大度(G)=max{d(v)| vV} G的最小度(G)=min{d(v)| vV} 例如 d(v5 )=3, d(v2 )=4, d(v1 )=4, (G)=4, (G)=1, v4是悬挂顶点, e7是悬挂边, e1是环