
第九章 集合的基数
第九章 集合的基数

定义9.1 设A,B是集合,如果存在着从A到B 的双射函数,就称A和B是等势的, 记作A≈B. 如果A不与B等势,则记作A光B·
定义9.1 设A,B 是集合,如果存在着从A到B 的双射函数,就称A和B是等势的, 记作A B . 如果A不与B等势,则记作A B .

例9.1 (1)Z≈N (2)NXN≈N (3)N≈Q (4)(0,1)≈R (5S)[0,1≈(0,1) (⑥对于任意a,b∈R,a≠b,0,1刂≈[a,b]
例9.1 (1) Z N (2) N×N N (3) N Q (4) (0,1) R (5) [0,1] (0,1) (6) 对于任意a,b R ,a ≠ b ,[0,1] [a,b]

构造从A到B的双射函数(续) A与自然数集合之间构造双射 方法:将A中元素排成有序图形,然后从第一个元素开始 按照次序与自然数对应 例7A=乙,B=N,构造双射f:A→B 将Z中元素以下列顺序排列并与N中元素对应: Z:0-11-22-33. ↓↓↓↓↓↓J N:0123456. 则这种对应所表示的函数是: fZ→N,f)=仁-2x-1 2x x≥0 x<0
构造从A到B的双射函数(续) A 与自然数集合之间构造双射 方法:将A中元素排成有序图形,然后从第一个元素开始 按照次序与自然数对应 例7 A=Z, B=N,构造双射 f:A→B 将Z中元素以下列顺序排列并与N中元素对应: Z:0 1 1 2 2 3 3 . ↓ ↓ ↓ ↓ ↓ ↓ ↓ N:0 1 2 3 4 5 6 . 2 1 0 2 0 Z , ( ) x x x x f: N f x

(4)(0,1)≈R 构造双射f:(0,1)→R 2x-1 f(x)=tanπ 2 易见f是单调上升的,且ranf=R
(4) (0,1) R 构造双射 f: (0,1) → R 易见 f 是单调上升的,且ran f =R 2 2 1 ( ) tan x f x

(5)[0,1山≈(0,1) 构造区间[0,1]与(0,1)之间1-1映射的 一个例子。我们知道全体有理数的集合是 可数的,于是(0,1)区间中的有理数是可数 的,不妨将它们排成a1,a2,an,的 形式。 而闭区间[0,1]比区间(0,1)多两个数0 和1,它们是有理数,于是可建立闭区间[0, 1]中的有理数到区间(0,1)中的有理数的1-1 映射o1:
(5) [0,1] (0,1) 构造区间[0,1]与(0,1)之间1-1映射的 一个例子。我们知道全体有理数的集合是 可数的,于是(0,1)区间中的有理数是可数 的,不妨将它们排成a1 , a2 , ., an , .的 形式。 而闭区间[0,1]比区间(0,1)多两个数0 和1,它们是有理数,于是可建立闭区间[0, 1]中的有理数到区间(0,1)中的有理数的1-1 映射1:

0,1,a1, a1,a2a3 a4’ .,ant2 令区间[0,1]中的无理数到区间(0,1)中的无理数 的1-1映射o,为自己对应自己。则映射0=01U02 为区间[0,1]到区间(0,1)的1-1映射。从而区间 [0,1]与(0,1)等势
令区间[0,1]中的无理数到区间(0,1)中的无理数 的1-1映射2为自己对应自己。则映射= 1∪2 为区间[0, 1]到区间(0,1)的1-1映射。从而区间 [0,1]与(0,1)等势。 0, 1, a1, a2,.,an,. . . a1,a2,a3, a4,., an+2,

定理9.1 (1)A≈A (2)若A≈B,则B≈A 3)若A≈B,B≈C,则A≈C
定理9.1 (1) A A (2) 若A B,则B A (3) 若A B, B C,则A C
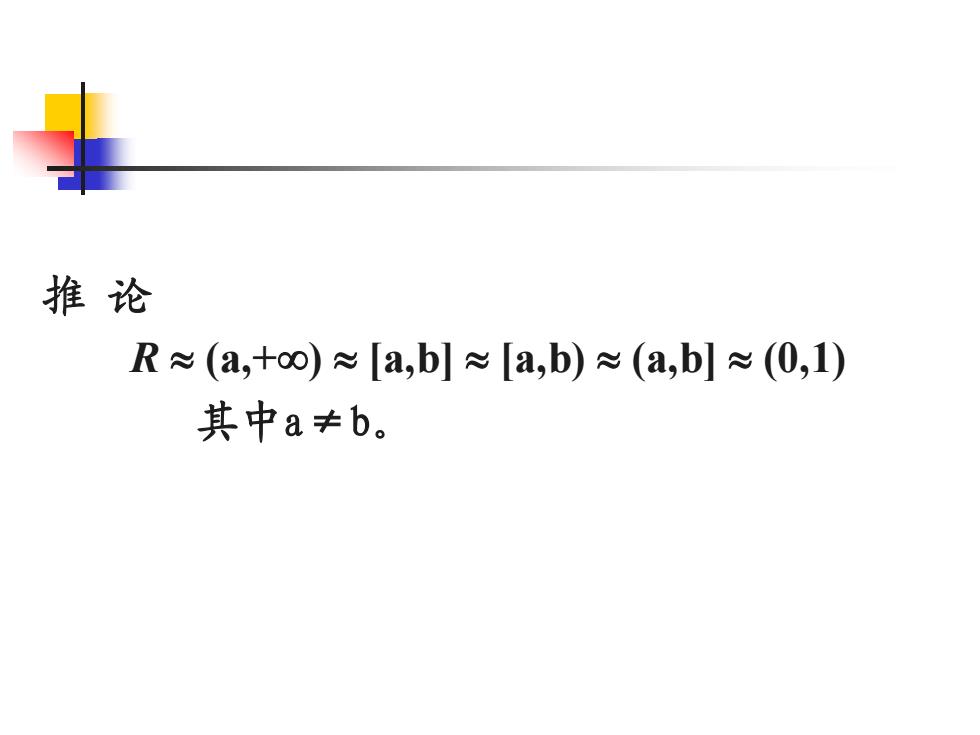
推论 R≈(a,+o∞)≈a,b]≈[a,b)≈(a,bl≈(0,1) 其中a≠b
推 论 R (a,+) [a,b] [a,b) (a,b] (0,1) 其中a≠b

定理9.2(康托尔定理) (1)N¥R (2)对任意集合A都有A*P(A)
定理9.2(康托尔定理) (1) N R (2) 对任意集合A都有 A P(A)