
第十三章格与布尔代数
第十三章 格与布尔代数

§13.1格的定义与性质 定义设是偏序集,如果Vx,yES, x,y}都有最小上界和最大下界,则称S关于 ≤构成一个格
定义 设是偏序集,如果 x,y∈S, {x,y}都有最小上界和最大下界, 则称S关于 ≼构成一个格. §13.1 格的定义与性质
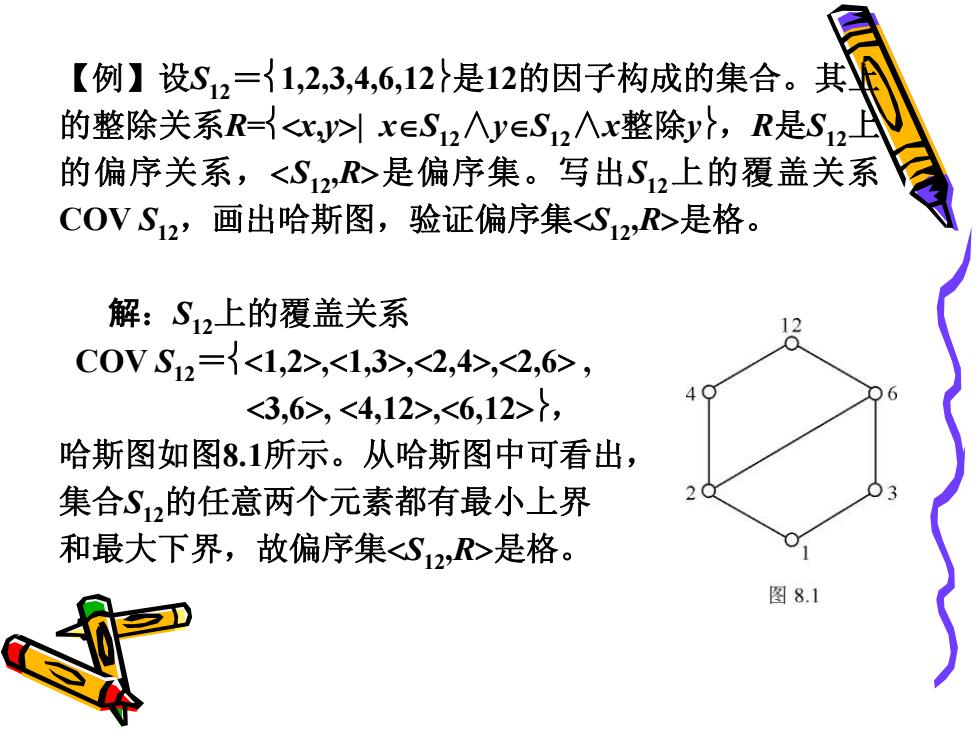
【例】设S12=了1,2,3,4,6,12是12的因子构成的集合。其 的整除关系R=lxES12个JyES12∧x整除y7,R是S12H 的偏序关系,,,,, ,,7, 哈斯图如图8.1所示。从哈斯图中可看出, 集合S2的任意两个元素都有最小上界 和最大下界,故偏序集<S12,R心是格。 图8.1
【例】设S12 =1,2,3,4,6,12是12的因子构成的集合。其上 的整除关系R=x,y| xS12∧yS12∧x整除y,R是S12上 的偏序关系,S12,R是偏序集。写出S12上的覆盖关系 COV S12,画出哈斯图,验证偏序集S12,R是格。 解:S12上的覆盖关系 COV S12 =1,2,1,3,2,4,2,6 , 3,6, 4,12,6,12, 哈斯图如图8.1所示。从哈斯图中可看出, 集合S12的任意两个元素都有最小上界 和最大下界,故偏序集S12,R是格

xVy表示x和y的最小上界 x∧y表示x和y的最大下界 V和∧在本章中只是格中的运算符,不表 示逻辑上的合取与析取
x∨y表示x和y的最小上界 x∧y表示x和y的最大下界. ∨和∧在本章中只是格中的运算符,不表 示逻辑上的合取与析取

例1设n为正整数,Sn为n的正因子的集合, D为整除关系,则构成格. Vx,yE Sn, xVy是x,y的最小公倍数[x,y],1cm(x,y) x∧y是x,y的最大公约数(x,y),gcd(x,y)
例1 设n为正整数,Sn为n的正因子的集合, D为整除关系,则构成格. x,y∈Sn, x∨y是x,y的最小公倍数[x,y],lcm(x,y) x∧y是x,y的最大公约数(x,y),gcd(x,y)
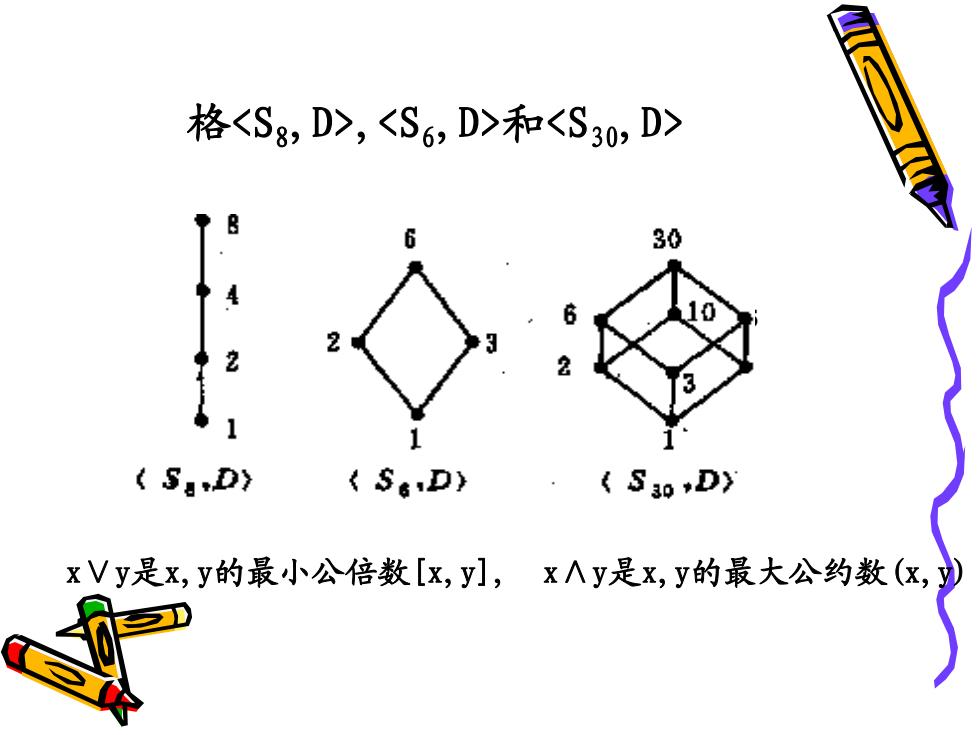
格,和 30 0 (SgD》 SD) 〈S30D〉 xVy是x,y的最小公倍数[x,y],x∧y是x,y的最大公约数(x,)
格,和 15 5 x∨y是x,y的最小公倍数[x,y], x∧y是x,y的最大公约数(x,y)
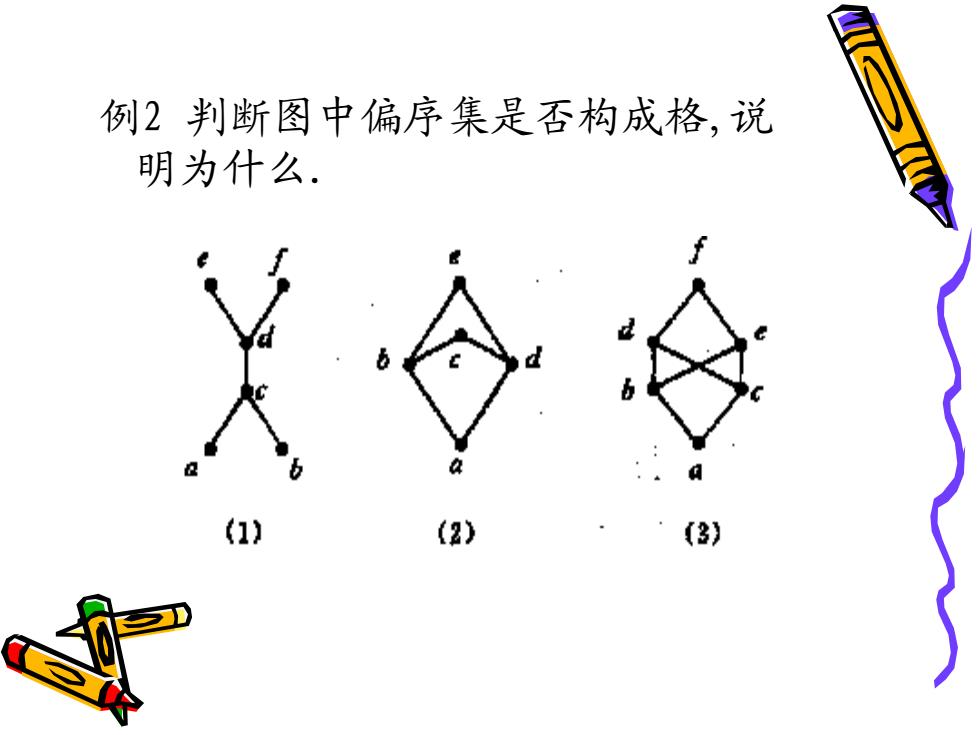
例2判断图中偏序集是否构成格,说 明为什么. 1ù (2)
例2 判断图中偏序集是否构成格,说 明为什么

定义设f是含有格中的元素以及符号,≤,君 V,∧的命题,令f*是将f中的≤改写成≥ 将≥改写成≤,V改写成∧,人改写成V 所得到的命题,称为的对偶命题. •格的对偶原理 若f对一切格为真,则f的对偶命题f*也对 一切格为真. 例3在格中有 (aVb)∧c≤c成立,则有 (a∧b)Vc≥c成立
•格的对偶原理 若f对一切格为真, 则f的对偶命题f*也对 一切格为真. 例3 在格中有 (a∨b)∧c≤c 成立,则有 (a∧b)∨c≥c 成立. 定义 设f是含有格中的元素以及符号=,≤,≥, ∨,∧的命题,令f *是将f中的≤改写成≥, 将≥改写成≤,∨改写成∧,∧改写成∨ 所得到的命题,称为f的对偶命题

定理设为格,则运算V和∧适合 交换律、结合律、幂等律和吸收律,即 (1)Va,b∈L有 aVb=bVa,a∧b=b∧a (2)Va,b,cEL有 (aVb)Vc=aV(bVc), (a∧b)∧c=a∧(b个c). (3)Va∈L有aVa=a,aΛa=a. 母a,bEL,有 aV(a∧b)=a,a∧(aVb)=a
定理 设为格,则运算∨和∧适合 交换律、结合律、幂等律和吸收律,即 (1)a,b∈L有 a∨b=b∨a, a∧b=b∧a (2) a,b,c∈L有 (a∨b)∨c=a∨(b∨c), (a∧b)∧c=a∧(b∧c). (3)a∈L 有 a∨a=a, a∧a=a. (4) a,b∈L,有 a∨(a∧b)=a, a∧(a∨b)=a

(2)Va,b,cEL有 (aVb)Vc=aV(bVc), (a∧b)∧c=a∧(b∧c). 证明 由最小上界的定义有 (aVb)Vc≥aVb≥a, (6.1) (aVb)Vc≥aVb≥b, (6.2) (aVb)Vc≥c. (6.3) 由式6.2和6.3得 (aVb)Vc≥bVc, (6.4) 再由式6.1和6.4得 (aVb)Vc≥aV(bVc), 同理可证 (aVb)Vc≤aV(bVc) 根据偏序的反对称性有 D(a Vb)Vc=aVbVc 似地可以证明 (a∧b)∧c=a∧(b∧c)
(2) a,b,c∈L有 (a∨b)∨c=a∨(b∨c), (a∧b)∧c=a∧(b∧c). 证明 由最小上界的定义有 (a∨b)∨c≥a∨b≥a, (6.1) (a∨b)∨c≥a∨b≥b, (6.2) (a∨b)∨c≥c. (6.3) 由式6.2和6.3得 (a∨b)∨c≥b∨c, (6.4) 再由式6.1和6.4得 (a∨b)∨c≥a∨(b∨c), 同理可证 (a∨b)∨c≤a∨(b∨c) 根据偏序的反对称性有 (a∨b)∨c=a∨b∨c 类似地可以证明 (a∧b)∧c=a∧(b∧c)