福州大学：《离散数学》课程教学资源（课件讲稿）第五章 阶逻辑等值演算与推理

第五章 一阶逻辑等值演算与推理 1

1 第五章 一阶逻辑等值演算与推理

§5.1一阶逻辑等值演算 ■等值式 ■基本等值式 ■量词否定等值式 ■量词辖域收缩与扩张等值式 ■量词分配等值式 2

2 §5.1一阶逻辑等值演算 等值式 基本等值式 量词否定等值式 量词辖域收缩与扩张等值式 量词分配等值式

等值式与基本等值式 在一阶逻辑中，有些命题可以有不同的符号化 形式。 例如：没有不呼吸的人。 取全总个体域时有下面两种不同的符号化形式： (1)3x(Fx)ΛGx) (2)x(Fx)→Gx) Fx):x是人，G(x):x要呼吸 3

3 等值式与基本等值式 在一阶逻辑中，有些命题可以有不同的符号化 形式。 例如：没有不呼吸的人。 取全总个体域时有下面两种不同的符号化形式： (1)   x (F(x) G(x)) (2) x (F(x)G(x)) F(x)：x是人， G(x)： x要呼吸

等值式与基本等值式 定义若A→B为逻辑有效式，则称A与B是等值的， 记作A一B,并称A一B为等值式. 基本等值式： 命题逻辑中16组基本等值式的代换实例 如，xFx)-→]yG0y)台一xFxV3yG0y) (xF)V3yGy)台xFx)A-yGy)等 消去量词等值式 设D={a1,42,0n} xA(x)台A(a1)A(a2)N.入A(an） xA(x)A(a )vA(a)v.VA(aj)

4 等值式与基本等值式 基本等值式: 命题逻辑中16组基本等值式的代换实例 如，xF(x)yG(y)  xF(x)yG(y) (xF(x)yG(y))  xF(x)yG(y) 等 消去量词等值式 设D={a1 ,a2 ,.,an } xA(x)A(a1 )A(a2 ).A(an ) xA(x)A(a1 )A(a2 ).A(an ) 定义 若AB为逻辑有效式，则称A与B是等值的， 记作 AB，并称AB为等值式

基本的等值式（续） 量词否定等值式 设Ax)是含x自由出现的公式 xA(x)台xA(c) 3xA(x)台VxA(x) 5

5 基本的等值式(续) 量词否定等值式 设A(x)是含x自由出现的公式  xA(x)  x  A(x)  xA(x)   x A(x)

基本等值式（续） 量词辖域收缩与扩张等值式 设A心)是含x自由出现的公式，B中不含x的出现 关于全称量词的： 关于存在量词的： x(AxVB)台xAx)vB 3x(Ax)VB)台3xA(x)vB x(AK)B)台xAx)AB 3x(Ax)ΛB)→3xA(x)AB x(A(x)>B)→3xA()→B 3x(Ax)→B)台xA(x)→B x(B→>A(x)→B→xA(x) 3x(B>A()台B→A(c) 6

6 基本等值式(续) 量词辖域收缩与扩张等值式 设A(x)是含x自由出现的公式，B中不含x的出现 关于全称量词的： x(A(x)B)xA(x)B x(A(x)B)xA(x)B x(A(x)B)xA(x)B x(BA(x))BxA(x) 关于存在量词的: x(A(x)B)xA(x)B x(A(x)B)xA(x)B x(A(x)B)xA(x)B x(BA(x))BxA(x)

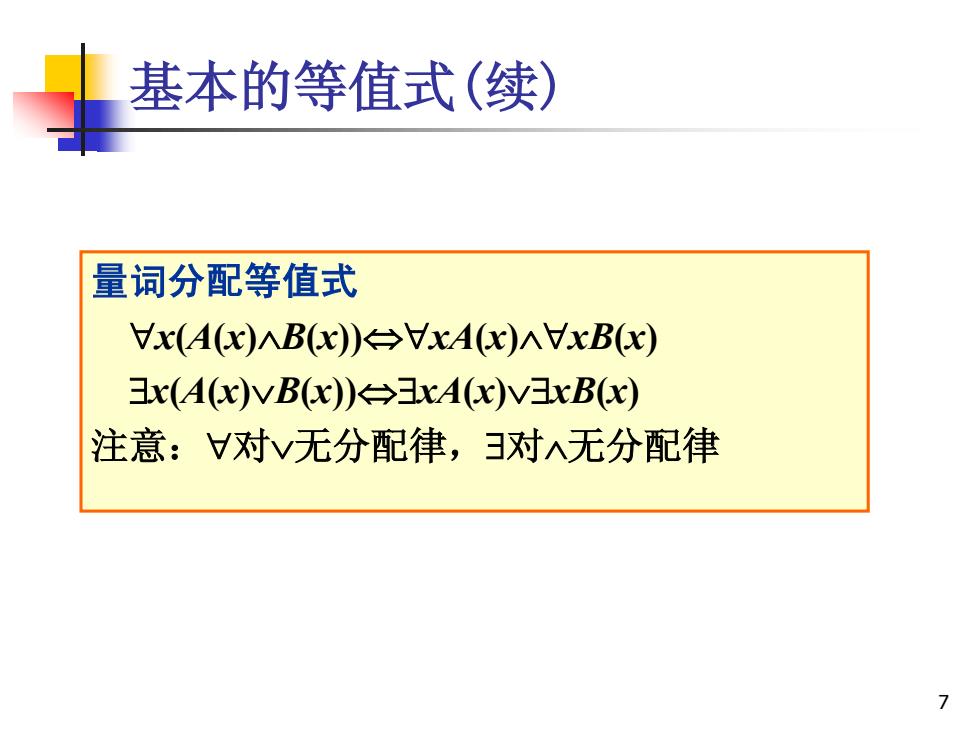
基本的等值式（续） 量词分配等值式 x(A(c)AB(x)台→xA(x)AxBx) x(A(x)vB(x))A(x)vB(x) 注意：V对无分配律，对入无分配律 7

7 基本的等值式(续) 量词分配等值式 x(A(x)B(x))xA(x)xB(x) x(A(x)B(x))xA(x)xB(x) 注意：对无分配律，对无分配律

基本的等值式（续） 例将下面命题用两种形式符号化 ()没有不犯错误的人 (2)不是所有的人都爱看电影 解()令Fx):x是人，Gc):x犯错误. x(F(x)-G(x)) 台x(Fx)→Gx) 请给出演算过程，并说明理由. (2)令Fx):是人，Gx):爱看电影 x(Fx)-→Gx) 台3x(Fx)Gx) 给出演算过程，并说明理由. 8

8 基本的等值式(续) 例 将下面命题用两种形式符号化 (1) 没有不犯错误的人 (2) 不是所有的人都爱看电影 解 (1) 令F(x)：x是人，G(x)：x犯错误. x(F(x)G(x)) x(F(x)G(x)) 请给出演算过程，并说明理由. (2) 令F(x)：x是人，G(x)：爱看电影. x(F(x)G(x)) x(F(x)G(x)) 给出演算过程，并说明理由

等值演算的三条原则 置换规则：若A一B,则(B)台A) 换名规则：将量词辖域中出现的某个约束变项的所 有出现及对应的指导变项，改成该量词辖域中未曾 出现过的个体变项符号，公式中其余部分不变，则 所得公式与原来的公式等值. 代替规则：对某自由出现的个体变项用与原公式 中所有个体变项符号不同的符号去代替，则所得公 式与原来的公式等值 9

9 等值演算的三条原则 置换规则：若AB, 则(B)(A) 换名规则: 将量词辖域中出现的某个约束变项的所 有出现及对应的指导变项，改成该量词辖域中未曾 出现过的个体变项符号，公式中其余部分不变，则 所得公式与原来的公式等值. 代替规则: 对某自由出现的个体变项用与原公式 中所有个体变项符号不同的符号去代替，则所得公 式与原来的公式等值

换名规则与代替规则 例 (1)VxF(x)>y(G(xy)-H(y)) →VzFz)-→3y(Gcy)Λ-H0y) (换名规则) (2)Vx(F(xy)>y(G(xy)H(x,))) 台x(Fx,)-→y(Gc,y)AHc,z)(代替规则) 10

10 换名规则与代替规则 例 (1) xF(x)y(G(x,y)H(y)) zF(z)y(G(x,y)H(y)) （换名规则） (2) x(F(x,y)y(G(x,y)H(x,z))) x(F(x,u)y(G(x,y)H(x,z))) ( 代替规则 )