
第十章 代数系统 10.1二元运算及其性质 10.2代数系统
10.1 二元运算及其性质 10.2 代数系统 第十章 代数系统

§10.1二元运算及其性质 定义设S是一个非空集合,称S×S到S的 函数f为S的一个二元(代数)运算. 问题 下面的映射是N×N到N上的二元运算吗? 1)f()=x+y 2)f()=x-y
§10.1 二元运算及其性质 定义 设S是一个非空集合,称S×S 到S的 函数f为S的一个二元(代数)运算. 问题 下面的映射是N×N到N上的二元运算吗? 1) f(x,y)= x+y 2) f(x,y)= x-y

验证一个运算是否为集合S上的二元 运算主要考虑两点: 1.S中任何两个元素都可以进行这 种运算,且运算结果惟一, 2.S中任何两个元素的运算结果都 属于S,即S对该运算是封闭的
验证一个运算是否为集合S上的二元 运算主要考虑两点: 1. S中任何两个元素都可以进行这 种运算,且运算结果惟一. 2. S中任何两个元素的运算结果都 属于S,即S对该运算是封闭的

例1非零实数集R*上的乘法、除法是R上的) 二元代数运算;加法和减法不是R*上的 二元代数运算,因为两个非零实数相加 或相减可能得出0 例2 设S是一个非空集合,p(S)是S的 幂集,则集合的交运算∩、并运算U是 (S)上的二元代数运算
例1 非零实数集R *上的乘法、除法是R *上的 二元代数运算;加法和减法不是R *上的 二元代数运算,因为两个非零实数相加 或相减可能得出0 例2 设S是一个非空集合,ρ(S) 是S的 幂集,则集合的交运算∩、并运算∪是 ρ(S)上的二元代数运算

例3判断下列集合上的关系是否为二元运算 ()N上的:加法、乘法 (2)Z上的:加法、减法、乘法 (3)设S={v2,·,an},:%=
例3 判断下列集合上的关系是否为二元运算 (1) N 上的:加法、乘法. (2) Z 上的:加法、减法、乘法. (3) 设 S = { a1 , a2 , . , an }, ai ∘aj = ai
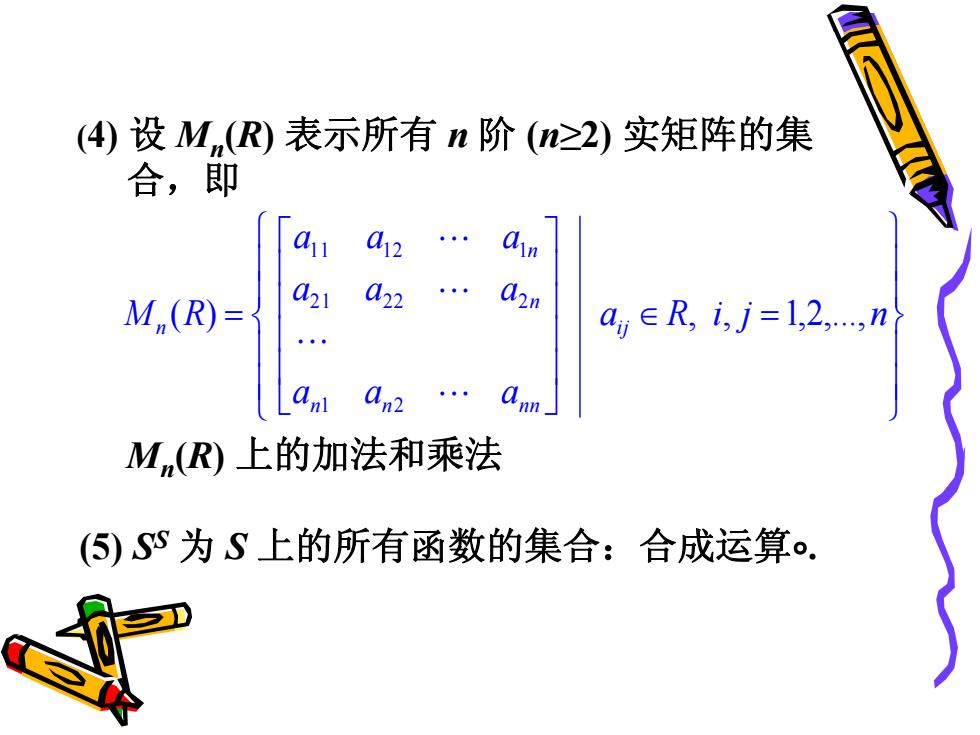
(4)设Mm(R)表示所有n阶(n≥2)实矩阵的集 合,即 a 12 Mn(R)=〈 d21 022 . a∈R,ij=1,2,n an2 Mn(R)上的加法和乘法 (⑤)Ss为S上的所有函数的集合:合成运算
(4) 设 Mn (R) 表示所有 n 阶 (n≥2) 实矩阵的集 合,即 Mn (R) 上的加法和乘法 (5) S S 为 S 上的所有函数的集合:合成运算∘. a R i j n a a a a a a a a a M R i j n n n n n n n ( ) , , 1,2,., 1 2 2 1 2 2 2 1 1 1 2 1

>代数运算是闭运算。 该运算具有很强的抽象性,不限于+,- *,/,意义很广泛。 类似地,可定义S的n元代数运算:Sn到S 的映射。 >S中元素任意性使a,b可以是同一个元素
代数运算是闭运算。 该运算具有很强的抽象性,不限于+,-, *,/,意义很广泛。 类似地,可定义S的n元代数运算: S n到S 的映射。 S中元素任意性使a,b可以是同一个元素

羽,.等东友示二完码 算,称为算符。 如f:S×S→S,f()=z 可利用算符简记为 Xoy=Z 表示二元或一元运算的方法: 公式、运算表 注意:在同一问题中不同的运算使用不同的算符
通常用,*,·, ‥‥等符号表示二元运 算,称为算符。 如 f:S×S→S, f(x,y)= z 可利用算符简记为 xy= z 表示二元或一元运算的方法: 公式、 运算表 注意:在同一问题中不同的运算使用不同的算符

公式表示 例3设R为实数集合,如下定义R上的二元运 算*: x,y∈R,X*y=X. 那么 3*4=3 0.5*(-3)=0.5 运算表(表示有穷集上的一元和二元运算)
公式表示 例3 设 R 为实数集合,如下定义 R 上的二元运 算 ∗: x, y∈R, x ∗ y = x. 那么 3 ∗ 4 = 3 0.5 ∗ (-3) = 0.5 运算表(表示有穷集上的一元和二元运算)

定义设S为集合,函数SS称为S上的 元运算,简称为一元运算。 例(1)Z,2和R上的一元运算:求相反数 (2)非零有理数集Q*,非零实数集R*上的一元 运算:求倒数 (3)复数集合C上的一元运算:求共轭复数 (④幂集P(S上,全集为S:求绝对补运算 (⑤)A为S上所有双射函数的集合,AcSS:求反 函数 在Mn(R)(n≥2)上,求转置矩阵
定义 设 S 为集合,函数 f:S→S 称为 S 上的一 元运算,简称为一元运算. 例 (1) Z, Q 和 R 上的一元运算: 求相反数 (2) 非零有理数集 Q*,非零实数集 R*上的一元 运算: 求倒数 (3) 复数集合 C 上的一元运算: 求共轭复数 (4) 幂集 P(S) 上, 全集为 S: 求绝对补运算~ (5) A 为 S 上所有双射函数的集合,AS S : 求反 函数 (6) 在 Mn (R) ( n≥2 )上,求转置矩阵