
第六章共形映射 历些毛子种枚大票 XIDIAN UNIVERSITY Conformal mapping 第六章 共形映射 本章从几何映射角度考察复变函数的性 质。在介绍共形映射概念的基础上,重点掌 握分式线性映射和几种初等解析函数的映射 性质。 第一节共形映射的概念 第二节分式线性映射 第三节 唯一决定分式线性映射的条件 第四节几个初等解析函数构成的映射 场论与复变函数Field Theory and Complex Variable Functions
场论与复变函数 Field Theory and Complex Variable Functions 2 第六章 共形映射 Conformal mapping 第六章 共形映射 本章从几何映射角度考察复变函数的性 质。在介绍共形映射概念的基础上,重点掌 握分式线性映射和几种初等解析函数的映射 性质。 第一节 共形映射的概念 第二节 分式线性映射 第三节 唯一决定分式线性映射的条件 第四节 几个初等解析函数构成的映射

第六章共形映射 历些毛子种技大” XIDIAN UNIVERSITY Conformal mapping 第一节 共形映射的概念 在几何意义下,复变函数将z平面中的曲线或者区域 映射到w平面中的曲线或者区域。转动角和伸缩率是两个重要 的概念。共形映射是一种具有保角性和伸缩率不变性的映射 。解析函数在导数不为0的点处都是共形映射。 场论与复变函数Field Theory and Complex Variable Functions
场论与复变函数 Field Theory and Complex Variable Functions 3 第六章 共形映射 Conformal mapping 第一节 共形映射的概念 在几何意义下,复变函数将z平面中的曲线或者区域 映射到w平面中的曲线或者区域。转动角和伸缩率是两个重要 的概念。共形映射是一种具有保角性和伸缩率不变性的映射 。解析函数在导数不为0的点处都是共形映射
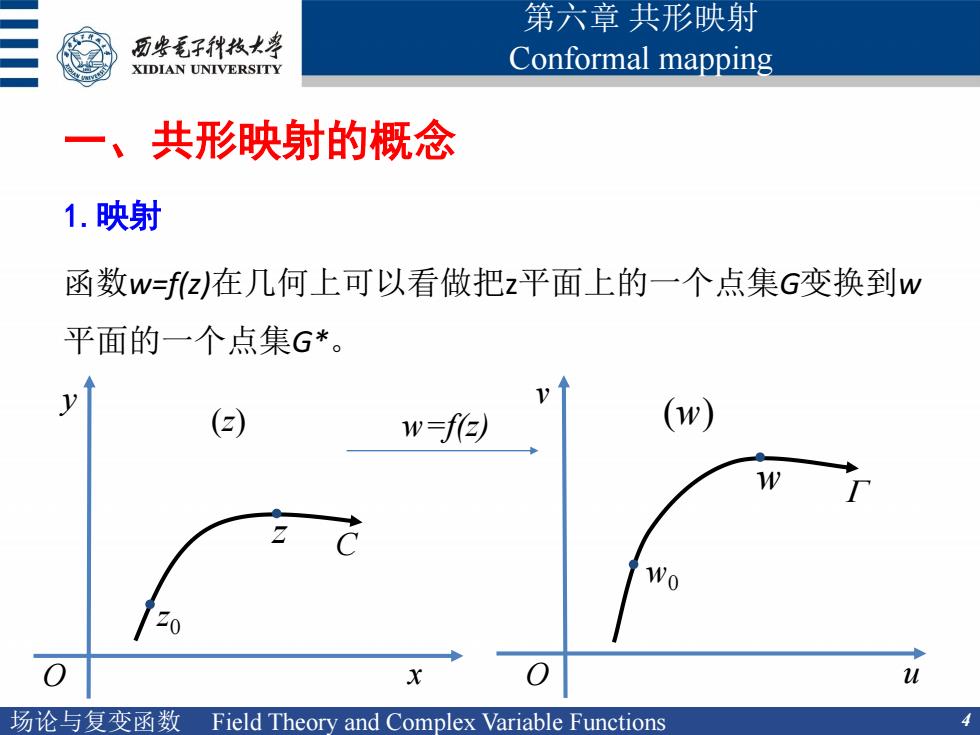
第六章共形映射 历些毛子代枚大票 XIDIAN UNIVERSITY Conformal mapping 共形映射的概念 1.映射 函数w=fz)在几何上可以看做把z平面上的一个点集G变换到w 平面的一个点集G*。 (2) w=f(z) (w) wo u 场论与复变函数Field Theory and Complex Variable Functions
场论与复变函数 Field Theory and Complex Variable Functions 4 第六章 共形映射 Conformal mapping 一、共形映射的概念 1.映射 函数w=f(z)在几何上可以看做把z平面上的一个点集G变换到w 平面的一个点集G* 。 x z0 z C (z) O O u G w0 w (w) y v w=f(z)

第六章共形映射 历安毛子代枚大学 XIDIAN UNIVERSITY Conformal mapping z平面内的一条有向连续曲线C可用参数方程 Z=z(t),a≤t≤b 表示,其正向取为t增大时点z移动的方向。 通过C上两点Po=z(ta)与P=zt。+△t)的做一条割线PP,其正向对 应于t增大的方向: C z(t+△t) Po z(to) 0 场论与复变函数Field Theory and Complex Variable Functions
场论与复变函数 Field Theory and Complex Variable Functions 5 第六章 共形映射 Conformal mapping z平面内的一条有向连续曲线C可用参数方程 z=z(t), a t b 表示, 其正向取为t增大时点z移动的方向。 通过C上两点P0=z(t0 )与P= z(t0+Dt)的做一条割线P0P,其正向对 应于t增大的方向: O x y z(t0) P0 P z(t0+Dt) C

第六章共形映射 历些毛子代枝大学 XIDIAN UNIVERSITY Conformal mapping 当点P沿C无限趋向于点P,割线PP的极限位置是C上P处的切 线。向量 z(to+△t)-z(to) z'(to)lim Λt0 △t 与割线PP的方向相同,与曲线C相切于点zo=zt),称为曲线C 在点P。=zt处的切向量 (B) (to z(0 场论与复变函数Field Theory and Complex Variable Functions
场论与复变函数 Field Theory and Complex Variable Functions 6 第六章 共形映射 Conformal mapping 当点P沿C无限趋向于点P0 , 割线P0P的极限位置是C上P0处的切 线。向量 与割线P0P的方向相同,与曲线C相切于点z0=z(t0 ),称为曲线C 在点P0=z(t0 )处的切向量. z(t0 ) z(a) z(b) z '(t0 ) C

第六章共形映射 历安毛子代枚大学 XIDIAN UNIVERSITY Conformal mapping 根据切向量的定义,可得: 1)Argz'(to)就是zo处C的切线正向与x轴正向间的夹角; 2) 相交于一点的两条曲线C与C2正向之间的夹角,就是它 们交点处两条切线正向间的夹角。 场论与复变函数Field Theory and Complex Variable Functions
场论与复变函数 Field Theory and Complex Variable Functions 7 第六章 共形映射 Conformal mapping 根据切向量的定义,可得: 1) Arg z '(t0 )就是z0处C的切线正向与x轴正向间的夹角; 2) 相交于一点的两条曲线C1与C2正向之间的夹角,就是它 们交点处两条切线正向间的夹角

第六章共形映射 历些毛子代枝大学 XIDIAN UNIVERSITY Conformal mapping 2.解析函数导数的几何意义 设函数w=fz)在区域D内解析,Z为D内的一点,且f(zo≠0.又设 C为z平面内通过点z的一条有向光滑曲线,其参数方程是: z=z(t),0≤t≤B, 它的正向相应于参数t增大的方向,且zo=z(to,z'(to≠0,toB, 则映射w=fz)将C映射成w平面内通过点w。fzo)的一条有向光 滑曲线)其参数方程是 w=f几z(t)],ost≤B 正向相应于参数t增大的方向. 场论与复变函数Field Theory and Complex Variable Functions 8
场论与复变函数 Field Theory and Complex Variable Functions 8 第六章 共形映射 Conformal mapping 2.解析函数导数的几何意义 设函数w=f(z)在区域D内解析, z0为D内的一点, 且f ‘(z0 )0. 又设 C为z平面内通过点z0的一条有向光滑曲线, 其参数方程是: z=z(t), atb, 它的正向相应于参数t增大的方向, 且z0=z(t0 ), z ’(t0 )0, a<t0<b. 则映射w=f(z)将C映射成w平面内通过点w0=f(z0 )的一条有向光 滑曲线G, 其参数方程是 w=f[z(t)], atb 正向相应于参数t增大的方向
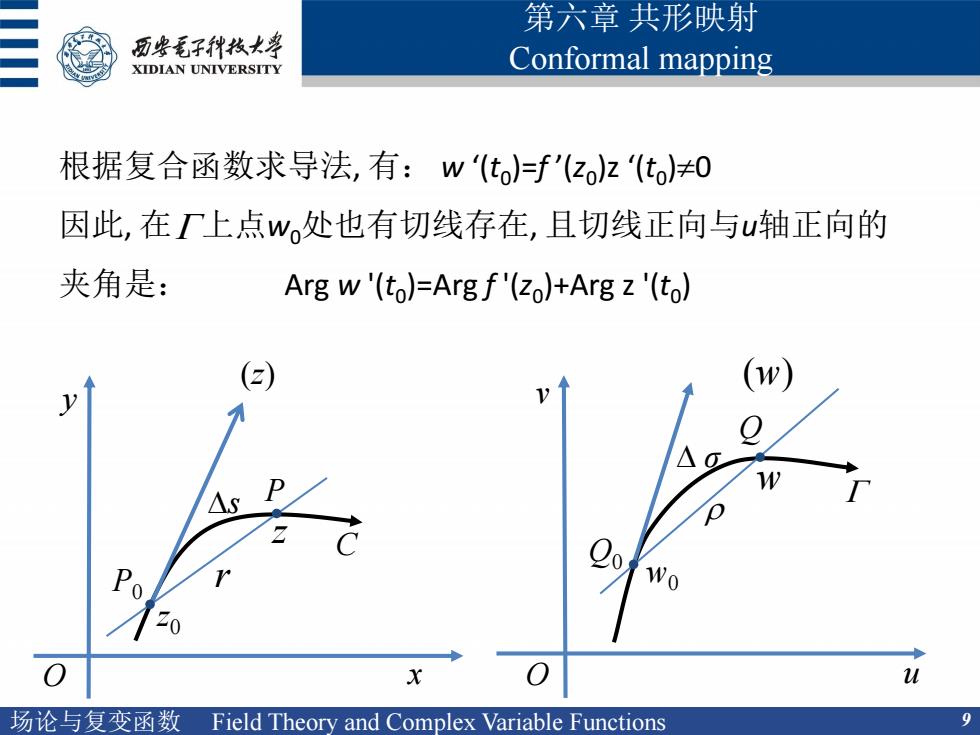
第六章共形映射 历安毛子代枚大等 XIDIAN UNIVERSITY Conformal mapping 根据复合函数求导法,有:w'(to)=f'(zoz《to≠0 因此,在T上点w处也有切线存在,且切线正向与u轴正向的 夹角是: Arg w'(to)=Arg f'(zo)+Arg z '(to) (z) y D u 场论与复变函数Field Theory and Complex Variable Functions
场论与复变函数 Field Theory and Complex Variable Functions 9 第六章 共形映射 Conformal mapping 根据复合函数求导法, 有: w ‘(t0 )=f ’(z0 )z ‘(t0 )0 因此, 在 上点w0处也有切线存在, 且切线正向与u轴正向的 夹角是: Arg w '(t0 )=Arg f '(z0 )+Arg z '(t0 ) x z0 P0 r z P Ds C (z) O G O u G w0 Q0 Q w r D σ (w) y v

第六章共形映射 历些毛子代找大学 XIDIAN UNIVERSITY Conformal mapping 或者有 Arg f'(Zo)=Arg w'(to)-Arg z'(to) (6.1.1) 如果将z点处的切线正向与w点处的切线正向之间的夹角理解 为曲线c经过w=f孔z)映射后在z处的转动角,则(6.1.1)式表明: 1)导数f'zo≠0的辐角Arg f '(z是曲线C经过w=fz映射后在z处 的转动角; 2)转动角的大小与方向跟曲线C的形状与方向无关,所以这种 映射具有转动角的不变性, 场论与复变函数Field Theory and Complex Variable Functions 10
场论与复变函数 Field Theory and Complex Variable Functions 10 第六章 共形映射 Conformal mapping 或者有 Arg f ‘(z0 ) =Arg w ’(t0 )-Arg z ‘(t0 ) (6.1.1) 如果将z0点处的切线正向与w0点处的切线正向之间的夹角理解 为曲线C经过w=f(z)映射后在z0处的转动角, 则(6.1.1)式表明: 1)导数f ’(z0 )0的辐角Arg f ‘(z0 )是曲线C经过w=f(z)映射后在z0处 的转动角; 2)转动角的大小与方向跟曲线C的形状与方向无关,所以这种 映射具有转动角的不变性
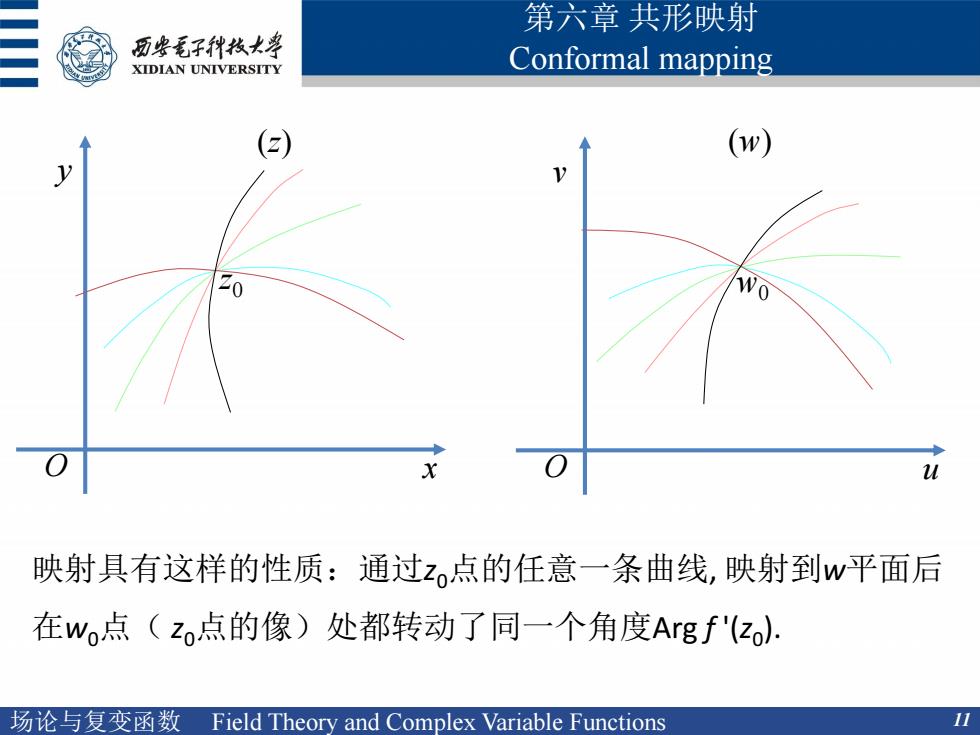
第六章共形映射 历安毛子代枚大学 XIDIAN UNIVERSITY Conformal mapping (w) y 映射具有这样的性质:通过z点的任意一条曲线,映射到w平面后 在w点(zo点的像)处都转动了同一个角度Argf'(zo). 场论与复变函数Field Theory and Complex Variable Functions 11
场论与复变函数 Field Theory and Complex Variable Functions 11 第六章 共形映射 Conformal mapping 映射具有这样的性质:通过z0点的任意一条曲线, 映射到w平面后 在w0点( z0点的像)处都转动了同一个角度Arg f '(z0 ). O x y O u v (z) (w) z0 w0