《随机矩阵》课程教学大纲 课程基本信息(Course Information) 学时 课程代码 MATH3707 48 学分 3 Hours) *课程名称 (中文)随机矩阵 (Course Name) (英文)Random matrix 课程类型 专业方向选修 (Course Type) 授课对象 (Target 本科生 Audience) 授课语言 (Language of 全中文 Instruction) 开课院系 数学科学学院 (School 先修课程 后续课程 (Prerequisite】 (post) “课程负贵人 课程网址 (Course (Instructor) Webpage) (中文300-500字,含课程性质、主要教学内容、课程教学日标等) 随机矩阵理论是研究随着维数趋向无穷时矩阵特征值统计规律的一门数学号 料,也是构造随机模型的基础理论之一。随机矩阵的发展可追溯到上世纪20 年代J.Wishart在多元统计分析中的工作以及上世纪50年代Wigner在量子力学 课程简介(中中的工作。在过去三十年中,随机矩阵理论的发展尤为迅速。目前,随机矩阵 理论不仅联系着许多重要的数学分支,包括概率统计、方程、代数表示论等, (Description) 并且广泛地应用于计算机和 程技术领域, 具有十分重要的数学和应用价值 本课程主要讲授几类重要的随机矩阵的历史发展和重要性质,包括Wigner矩卧 和样本协方差矩阵的半圆率,Marcenko-Pastur分布律,极值特征值,以及线性 谱统计量的中心极限定理等重要性质。课程旨在帮助学生了解随机矩阵的主要 数学结果和数学思想,提高学生的数学论证能力。 (英文300-500字) 课程简介(英 文) The central topic of random matrix theory is to study the statistical property of the values of random matrices when the imension tends to infinity.Random
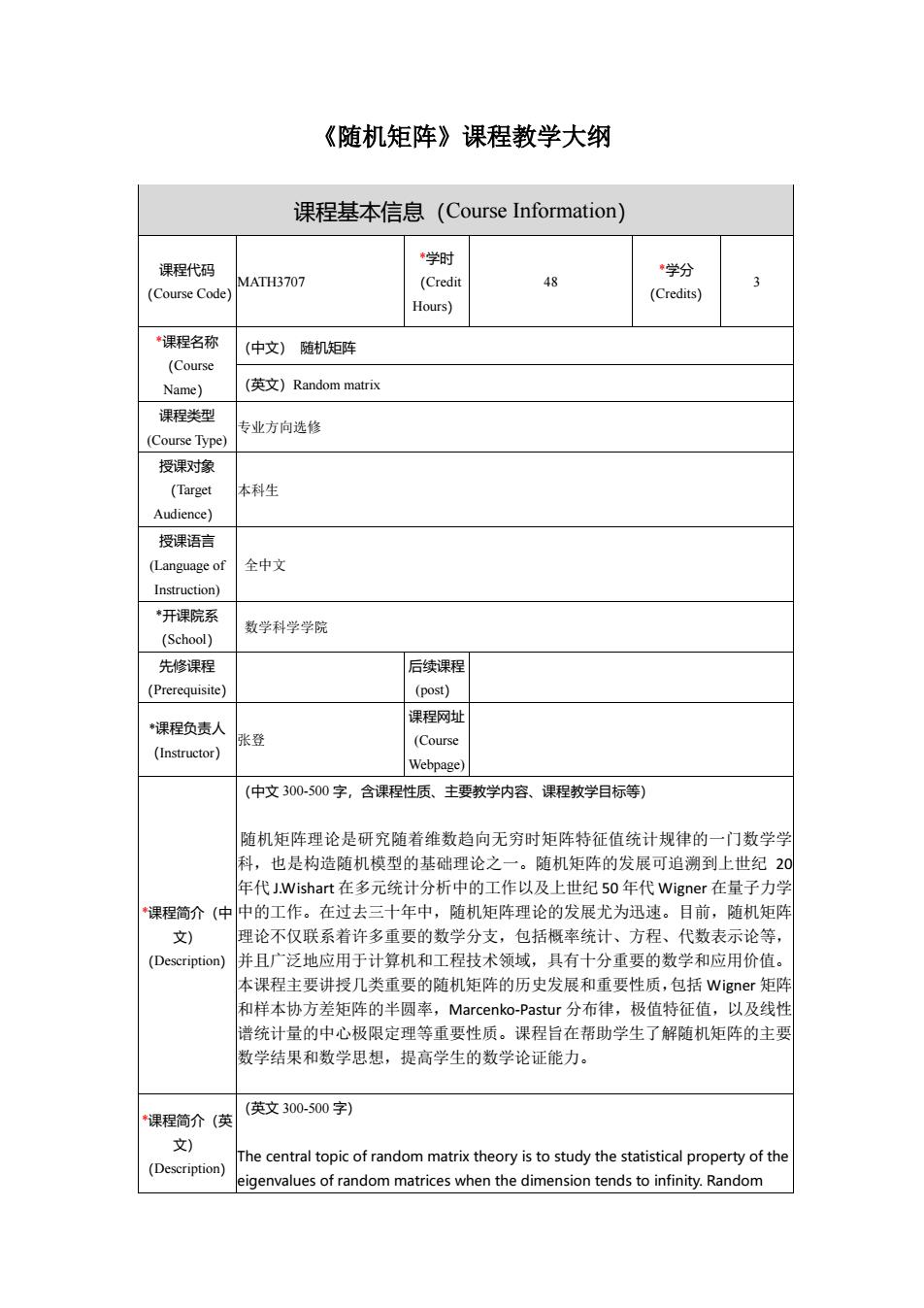
《随机矩阵》课程教学大纲 课程基本信息(Course Information) 课程代码 (Course Code) MATH3707 *学时 (Credit Hours) 48 *学分 (Credits) 3 *课程名称 (Course Name) (中文) 随机矩阵 (英文)Random matrix 课程类型 (Course Type) 专业方向选修 授课对象 (Target Audience) 本科生 授课语言 (Language of Instruction) 全中文 *开课院系 (School) 数学科学学院 先修课程 (Prerequisite) 后续课程 (post) *课程负责人 (Instructor) 张登 课程网址 (Course Webpage) *课程简介(中 文) (Description) (中文 300-500 字,含课程性质、主要教学内容、课程教学目标等) 随机矩阵理论是研究随着维数趋向无穷时矩阵特征值统计规律的一门数学学 科,也是构造随机模型的基础理论之一。随机矩阵的发展可追溯到上世纪 20 年代 J.Wishart 在多元统计分析中的工作以及上世纪 50 年代 Wigner 在量子力学 中的工作。在过去三十年中,随机矩阵理论的发展尤为迅速。目前,随机矩阵 理论不仅联系着许多重要的数学分支,包括概率统计、方程、代数表示论等, 并且广泛地应用于计算机和工程技术领域,具有十分重要的数学和应用价值。 本课程主要讲授几类重要的随机矩阵的历史发展和重要性质,包括 Wigner 矩阵 和样本协方差矩阵的半圆率,Marcenko-Pastur 分布律,极值特征值,以及线性 谱统计量的中心极限定理等重要性质。课程旨在帮助学生了解随机矩阵的主要 数学结果和数学思想,提高学生的数学论证能力。 *课程简介(英 文) (Description) (英文 300-500 字) The central topic of random matrix theory is to study the statistical property of the eigenvalues of random matrices when the dimension tends to infinity. Random

matrix theory is one of the basic theories in random models.It originates from the statistic works of Wishart and alsofrom the physical work of Wigner in ,the theory of random matrices developed rapidly in theast three decades.Nowadays,random matrix theory has deep connections with many important mathematical theories,including probability theory.statistics,differential equations and representation theory.Moreover,it also has wide applications in Thus,random matrix theo importance.This course ill present some important backgroundnd of random matrix theory.It will focus on the important properties of two random matrices,namely the Wigner matrix and the sample covariance matrix,including the semi-cirdle law,the Marcenko-Pastur law,extreme eigenvalues and the central limit theorems of linear spectral statistics.During this lecture,the students will learn ome main results and ideas in random matrix theory and receive therigorou nathematical training 课程目标与内容(Course objectives and contents) 结合本校办学定位、学生情况、专业人才培养要求,具体描述学习本课程后应该达到的知识 能力、素质、价值水平 “课程目标 (Course Object) 1,了解随机矩阵的历史发展和重要实际应用,了解随机矩阵的数学思想(A4) 2.掌握Wgr矩阵和样本协方差矩阵等重要随机矩阵的基本性质,提高抽象思维的能力, 培养深厚的基础理论和严谛的数学论证能力(B1) 章节教学内容(要点) 学时 教学形式 作业及考核要课程思玫酷对应课程目 求 入点 标 示例 教学内容进度 通过学习 安排及对应课 培养学生 计算经验盟 一丝不 程目标(Class 1 背景介绍 2 讲课 A4,B1 Schedule& 分布 苟、认真 Requirements 严速的门 作风 Course Objectives】 掌握Wigner 诵讨学习 矩阵、样本协 方差矩阵、 培养学生 极限谱分布 讲课 “丝不 A4,B1 24 积矩阵的极 限谱分布,以 苟、认真 及圆律 严谨的工 作风
matrix theory is one of the basic theories in random models. It originates from the statistic works of J. Wishart in 1920's and also from the physical work of Wigner in 1950's.In particular, the theory of random matrices developed rapidly in the last three decades. Nowadays, random matrix theory has deep connections with many important mathematical theories, including probability theory, statistics, differential equations and representation theory. Moreover, it also has wide applications in computation science and engineering. Thus, random matrix theory is of significant importance. This course will present some important background and applications of random matrix theory. It will focus on the important properties of two random matrices, namely the Wigner matrix and the sample covariance matrix, including the semi-circle law, the Marcenko-Pastur law, extreme eigenvalues and the central limit theorems of linear spectral statistics. During this lecture, the students will learn some main results and ideas in random matrix theory and receive the rigorous mathematical training. 课程目标与内容(Course objectives and contents) *课程目标 (Course Object) 结合本校办学定位、学生情况、专业人才培养要求,具体描述学习本课程后应该达到的知识、 能力、素质、价值水平。 1.了解随机矩阵的历史发展和重要实际应用,了解随机矩阵的数学思想(A4) 2.掌握 Wigner 矩阵和样本协方差矩阵等重要随机矩阵的基本性质,提高抽象思维的能力, 培养深厚的基础理论和严谨的数学论证能力(B1) *教学内容进度 安排及对应课 程目标 (Class Schedule & Requirements & Course Objectives) 章节 教学内容(要点) 学时 教学形式 作业及考核要 求 课程思政融 入点 对应课程目 标 示例: 1 背景介绍 2 讲课 计算经验谱 分布 通过学习 培养学生 一丝不 苟、认真 严谨的工 作风 A4,B1 2 极限谱分布 24 讲课 掌握 Wigner 矩阵、样本协 方差矩阵、乘 积矩阵的极 限谱分布,以 及圆律 通过学习 培养学生 一丝不 苟、认真 严谨的工 作风 A4,B1
了解Wigner 矩阵和样本 通过学习 协方差矩 培养学生 极值特征值 丝不 极值特征值 6 讲课 的基本概念苟、认真 A4,B1 和 亚苗的工 Tracy-Widom 作风 分布 掌捏Wigner通过学习 矩阵和样本培养学生 线性谱统计量的 协方差矩阵 丝不 4 中心极限定理 16 讲课 线性谱统计、认 A4,B1 量的中心极能谨的工 限定理 作风 注1:建议按照教学周周学时综排 注2:相应章节的课程思政融入点根据实际情况填写 考核方式 平时作业30%+期末考试70% (Grading) “教材或参考资 Bai,Zhidong;Fang,Zhaoben;Liang,Ying-Chang,Spectral theory of large ension. atrices ons to wirelessco finance statistics.Random matrix theory and its applications.World Scientifi Other Materials) Publishing Co.Pte.Ltd.,Hackensack,NJ;University of Science and Technology of China Press,Hefei,2014.xii+220 pp. 其它(More) 备注(Notes) 备注说明: 1.带*内容为必填项 2.课程简介字数为300-500字:课程大纲以表述清楚教学安排为宜,字数不限
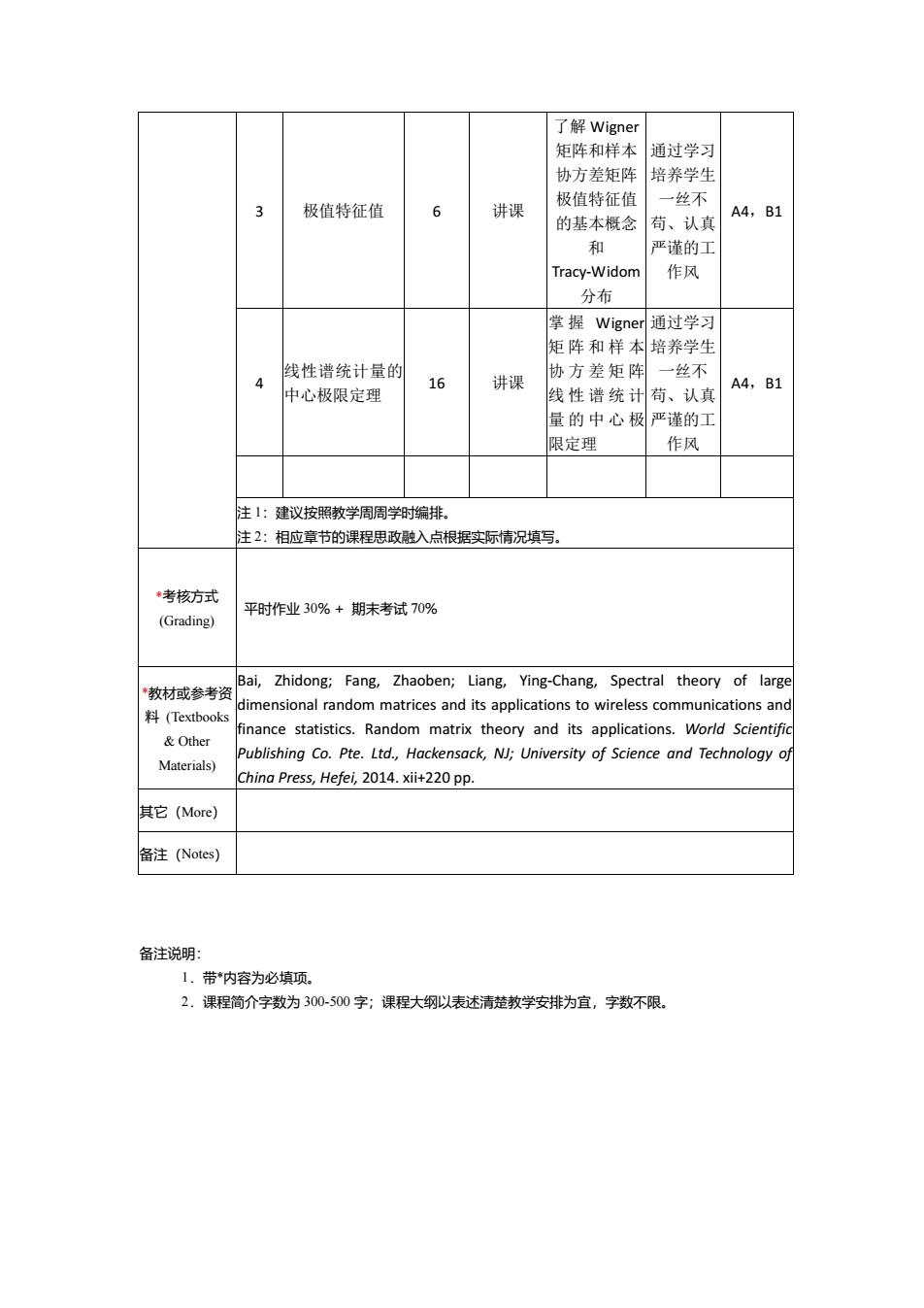
3 极值特征值 6 讲课 了解 Wigner 矩阵和样本 协方差矩阵 极值特征值 的基本概念 和 Tracy-Widom 分布 通过学习 培养学生 一丝不 苟、认真 严谨的工 作风 A4,B1 4 线性谱统计量的 中心极限定理 16 讲课 掌 握 Wigner 矩阵和样本 协方差矩阵 线性谱统计 量的中心极 限定理 通过学习 培养学生 一丝不 苟、认真 严谨的工 作风 A4,B1 注 1:建议按照教学周周学时编排。 注 2:相应章节的课程思政融入点根据实际情况填写。 *考核方式 (Grading) 平时作业 30% + 期末考试 70% *教材或参考资 料 (Textbooks & Other Materials) Bai, Zhidong; Fang, Zhaoben; Liang, Ying-Chang, Spectral theory of large dimensional random matrices and its applications to wireless communications and finance statistics. Random matrix theory and its applications. World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ; University of Science and Technology of China Press, Hefei, 2014. xii+220 pp. 其它(More) 备注(Notes) 备注说明: 1.带*内容为必填项。 2.课程简介字数为 300-500 字;课程大纲以表述清楚教学安排为宜,字数不限