《流形上的微积分》课程教学大纲 课程基本信息(Course Information) 学时 课程代码 MATH2450 (Course Cod ( Hours) *课程名称 (中文)流形上的徽积分 (Course Name) 课程类型 专业方向选修 (Course Type) 授课对橡 本科生 Audience) 授课语言 (Language of 双语 Instruction) “开课院系 数学科学学院、致远学院 (School) 先修课程 数学分析,高等代数 后续课程 (Prerequisite) (p0) *课程负责人 课程网 杨义虎 (Course (Instructor) Webpage) (中文300-500字,含课程性质、主要教学内容、课程教学日标等) 课程简介(中 本课程为夏季学期设计,四周,32课时。力图让学生掌握微分流形上的初步 (Description) 内容,如微分流形的定义,微分形式及其积分,Stokes定理及Poincare引理 等 (英文300-500字) This course is planned for summer school,totally 4 weeks and 32 hours.Its aim is e.B.defin tion,differential f forms and their integrals,Stokes theorem and Poincare (Description) lemma etc
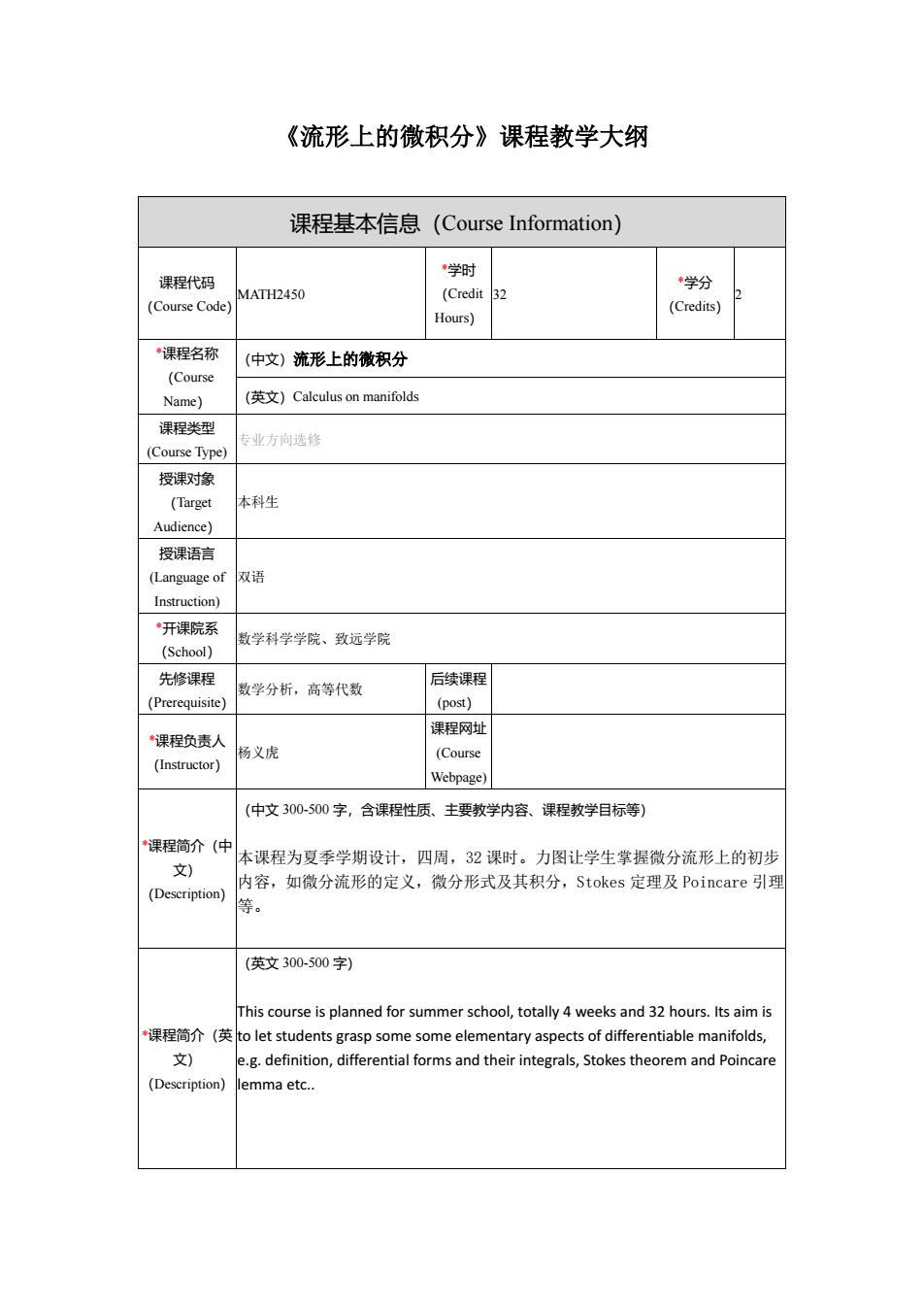
《流形上的微积分》课程教学大纲 课程基本信息(Course Information) 课程代码 (Course Code) MATH2450 *学时 (Credit Hours) 32 *学分 (Credits) 2 *课程名称 (Course Name) (中文)流形上的微积分 (英文)Calculus on manifolds 课程类型 (Course Type) 专业方向选修 授课对象 (Target Audience) 本科生 授课语言 (Language of Instruction) 双语 *开课院系 (School) 数学科学学院、致远学院 先修课程 (Prerequisite) 数学分析,高等代数 后续课程 (post) *课程负责人 (Instructor) 杨义虎 课程网址 (Course Webpage) *课程简介(中 文) (Description) (中文 300-500 字,含课程性质、主要教学内容、课程教学目标等) 本课程为夏季学期设计,四周,32 课时。力图让学生掌握微分流形上的初步 内容,如微分流形的定义,微分形式及其积分,Stokes 定理及 Poincare 引理 等。 *课程简介(英 文) (Description) (英文 300-500 字) This course is planned for summer school, totally 4 weeks and 32 hours. Its aim is to let students grasp some some elementary aspects of differentiable manifolds, e.g. definition, differential forms and their integrals, Stokes theorem and Poincare lemma etc
课程目标与内容(Course objectives and contents) 本课程的目标是力图让学生掌握微分流形上的初步内容,如微分流形的定义, 微分形式及其积分,Stokes定理及Poincare引理等。 *课程目标 1,培养学生加何伸用微积分作为工县来研究空间曲线曲面的几何问 Course Objec A4,A5,B2,B3 2 培养学生的几何直观,空间想象能力A4,A5 3, 同时为将来进一步学习更高深的几何内容打下坚实的基础,特别希望学生 脑子里有大量曲面方面的例子(A3引,. 章节 作业及考核要课程思政融对应课 教学内容(要点) 学时 教学形式 求 入点 程目标 第一章 .欧氏空间(区域》 课堂教学 上的微分形式 微分流形 2.1.微分流形、局剖 坐标系、微分结构、 课堂教学 ,2, 每次课堂 微分流形例子 教学后有课外 2.2.切(余切)空间、 通过课程学 作业。要求独 可尚函粉与可微时 习和平时作 安排及对应课 黑及它们的微分:切 果堂教学 立完成 程目标(Clas 有时布 业以及用老 向量场及李括号 综合性思考 题,培养号 Schedule& 2.3.流形上外微分 Requirements& 题,学生要经生一丝不 Course 式、外微分算子及比 简、认真折 一音 性质: de Rham上同 课堂教学 过认真思考 谨的工作作 Objectives 相互讨论或查 阅资料等方 风培养学 2.4.子流形,流形的 才能解 生刻苦务 浸入、嵌入:流形的 定向,带边流形,单 课堂教学 安排习题史意志 强的生活态 课,对作业中 位分解 度。 的问题集中进 .流形上的积分 行讲解 第三章3.1.微分形式的积 课堂教学 3.2.Stokes定理 课堂教学 .2 .3.Poincare引理 课常教学
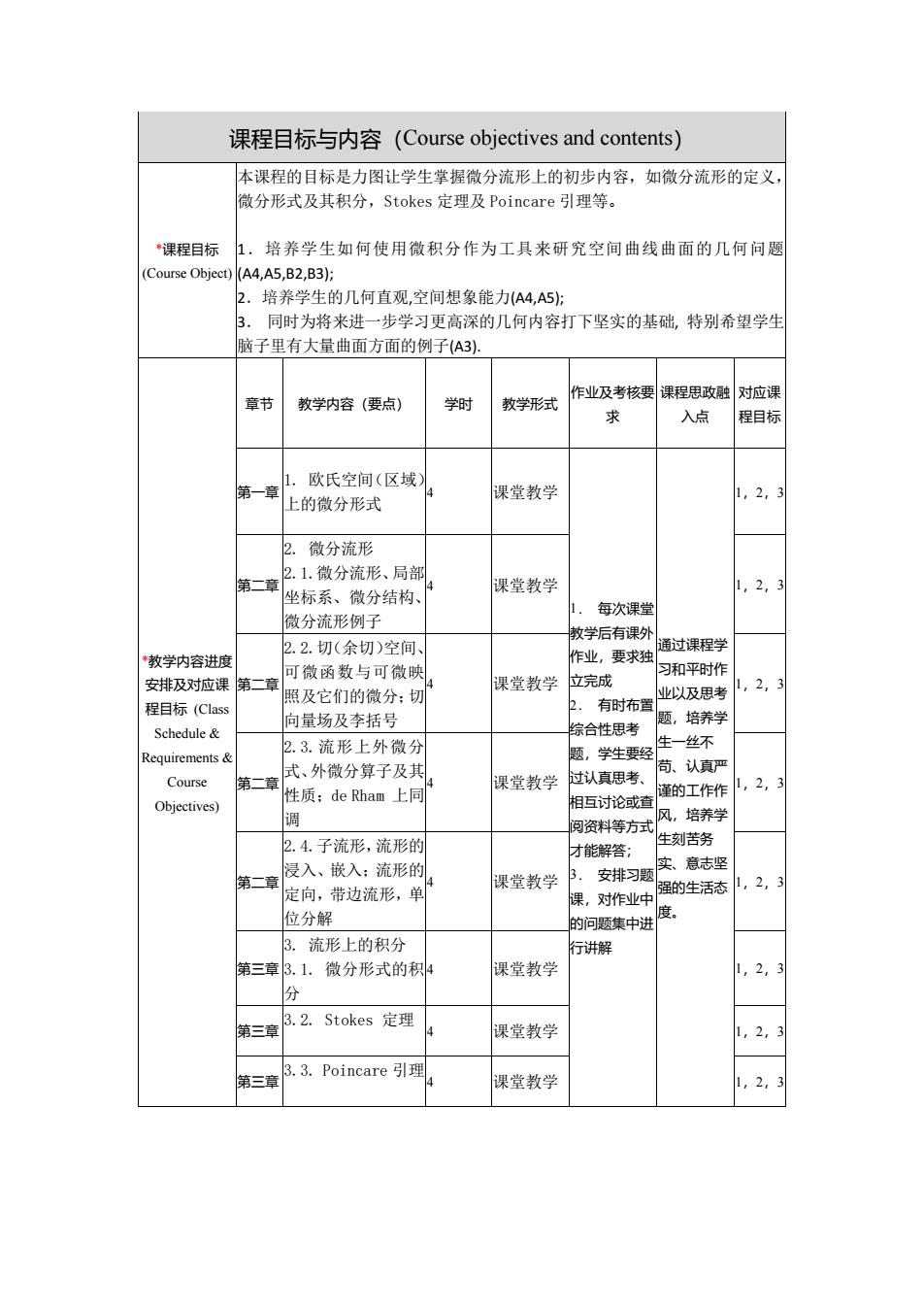
课程目标与内容(Course objectives and contents) *课程目标 (Course Object) 本课程的目标是力图让学生掌握微分流形上的初步内容,如微分流形的定义, 微分形式及其积分,Stokes 定理及 Poincare 引理等。 1.培养学生如何使用微积分作为工具来研究空间曲线曲面的几何问题 (A4,A5,B2,B3); 2.培养学生的几何直观,空间想象能力(A4,A5); 3. 同时为将来进一步学习更高深的几何内容打下坚实的基础, 特别希望学生 脑子里有大量曲面方面的例子(A3). *教学内容进度 安排及对应课 程目标 (Class Schedule & Requirements & Course Objectives) 章节 教学内容(要点) 学时 教学形式 作业及考核要 求 课程思政融 入点 对应课 程目标 第一章 1. 欧氏空间(区域) 上的微分形式 4 课堂教学 1. 每次课堂 教学后有课外 作业,要求独 立完成 2. 有时布置 综合性思考 题,学生要经 过认真思考、 相互讨论或查 阅资料等方式 才能解答; 3. 安排习题 课,对作业中 的问题集中进 行讲解 通过课程学 习和平时作 业以及思考 题,培养学 生一丝不 苟、认真严 谨的工作作 风,培养学 生刻苦务 实、意志坚 强的生活态 度。 1,2,3 第二章 2. 微分流形 2.1.微分流形、局部 坐标系、微分结构、 微分流形例子 4 课堂教学 1,2,3 第二章 2.2.切(余切)空间、 可微函数与可微映 照及它们的微分;切 向量场及李括号 4 课堂教学 1,2,3 第二章 2.3.流形上外微分 式、外微分算子及其 性质;de Rham 上同 调 4 课堂教学 1,2,3 第二章 2.4.子流形,流形的 浸入、嵌入;流形的 定向,带边流形,单 位分解 4 课堂教学 1,2,3 第三章 3. 流形上的积分 3.1. 微分形式的积 分 4 课堂教学 1,2,3 第三章 3.2. Stokes 定理 4 课堂教学 1,2,3 第三章 3.3. Poincare 引理 4 课堂教学 1,2,3

*考核方式 成绩构成)平时50%,期末509 (Grading) 参考书目: 教材域参考资[l】Manfredo P.do Carmo,Differential Forms and Application (TextbooksUniversitext,Springer &Other [2]陈省身、陈维桓,微分几何讲义,北京大学出版社,1983 Materials) [3]F.W.Warner,Foundations of Differentiable Manifolds and Lie Groups,GTM 94,Springer-Verlag 1983. 其它(More) 备注(Notes) 备注说明: 1.带内容为必填项。 2.课程简介字数为30-500字:课程大纲以表述清楚教学安排为宜,字数不限
*考核方式 (Grading) (成绩构成)平时 50%,期末 50% *教材或参考资 料 (Textbooks & Other Materials) 参考书目: [1] Manfredo P. do Carmo, Differential Forms and Application, Universitext, Springer [2] 陈省身、陈维桓,微分几何讲义,北京大学出版社, 1983 [3] F. W. Warner, Foundations of Differentiable Manifolds and Lie Groups, GTM 94, Springer-Verlag 1983. 其它(More) 备注(Notes) 备注说明: 1.带*内容为必填项。 2.课程简介字数为 300-500 字;课程大纲以表述清楚教学安排为宜,字数不限