
《代数拓扑》课程教学大纲 课程基本信息(Courselnformation) 课程代码 学时 MATH4406 (Credit 48 学分 (CourseCode Hours) (Credits) 课程名称 (中文)代数拓扑 (Course Name) (英文)AlgebraicTopology 课程类型 (CourseType) 专业方向选修 授课对橡 (Target 本科生 Audience) 授课语言 (Languag 中文或英文 Instruction) *开课院系 数学科学学院 (School) 先修课程 基础拓扑,抽象代数 后续课程 几何拓扑 (Prerequisite) (post) 课程网址 课程负责人 张光连 (Course无 (Instructor) Webpage) (中文300-500字,含课程性质、主要教学纳容、课程教学目标等) 文是为木科生准冬的一个学期的课程。在木课程中,我们系抽处理奇异园调、上园调 are对偶。我们的目标是给这些主塑 个常标准的经典方法。此外,我们还起向学生 绍范砖理论和单纯集的基本语言,它们在数学中非常有用,并且在代数拓扑中找到了它 的第一个真正的表现形式:出于类似的原因,我们还想强调同调代数的方法。为了证明 课程简介 (中废加莱对偶,我们系统地讨论了相对帽积和切赫上同调。 (Description)
《代数拓扑》课程教学大纲 课程基本信息(CourseInformation) 课程代码 (CourseCode) MATH4406 *学时 (Credit Hours) 48 *学分 (Credits) 3 *课程名称 (Course Name) (中文)代数拓扑 (英文)AlgebraicTopology 课程类型 (CourseType) 专业方向选修 授课对象 (Target Audience) 本科生 授课语言 (Languageof Instruction) 中文或英文 *开课院系 (School) 数学科学学院 先修课程 (Prerequisite) 基础拓扑,抽象代数 后续课程 (post) 几何拓扑 *课程负责人 (Instructor) 张光连 课程网址 (Course Webpage) 无 *课程简介(中 文) (Description) (中文300-500 字,含课程性质、主要教学内容、课程教学目标等) 这是为本科生准备的一个学期的课程。在本课程中,我们系统地处理奇异同调、上同调和 Poicare对偶。我们的目标是给这些主题一个非常标准的经典方法。此外,我们还想向学生介 绍范畴理论和单纯集的基本语言,它们在数学中非常有用,并且在代数拓扑中找到了它们 的第一个真正的表现形式;出于类似的原因,我们还想强调同调代数的方法。为了证明 庞加莱对偶,我们系统地讨论了相对帽积和切赫上同调
(英文300-500字) Theaimisto makethisatextthatcan beusedinonesemesteratundergraduatelevel In this course we systematically deals with singular homology and cobome Poicareduality.Our goal was to give a pretty standard classical approac to thes Moreover,we wanted tointroducestudentsto 文) usefulthroughoutmathematicsandfindingtheirfirstrealmanifestationsinalgebraictonology we als (Description) 课程目标与内容(Courseobjectivesandcontents) 要求学生堂握同调和上同调的概念、以及基本计算方法,(A3.B1) 课程目标 2要求学生理解范畴理论和单纯集的基本语言。(3,B1,) ,要求学生理解庞加菜对偶的证明,并且能够利用废加莱对偶处理一些问题。(3,2,C1 教学内 章节容(便 教学目标 学时 教学形式 作业及 课程思政融入对应课程 核要求 点 标 点) “敦学内容进度 h. 章提同 安排及对应课 程目标Class Schedule 问调的 后 概念、其 与课后作业培 周3 本理论.20 面授 习题 养学生一丝不A3,B1B2 ves) 态度」
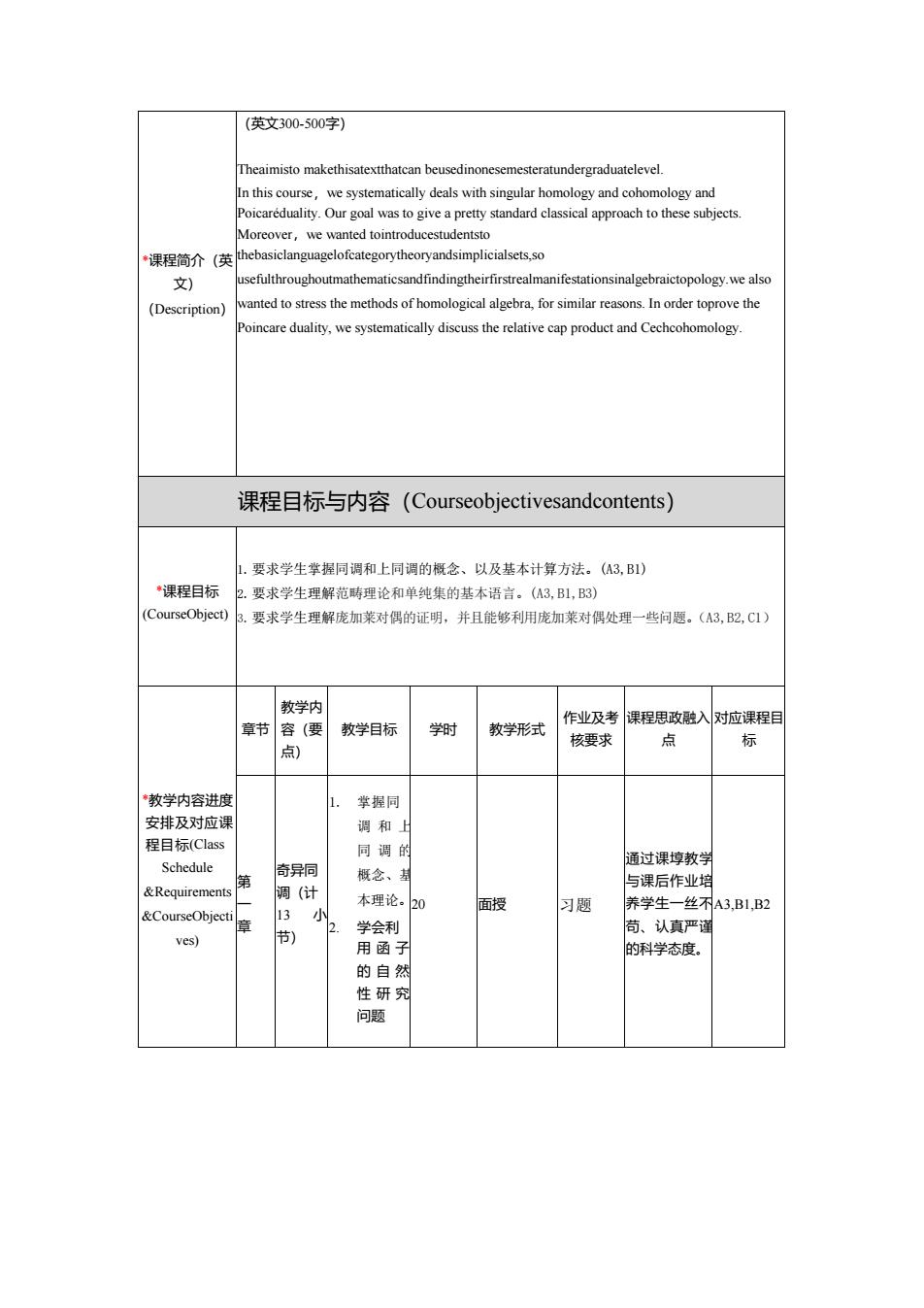
*课程简介(英 文) (Description) (英文300-500字) Theaimisto makethisatextthatcan beusedinonesemesteratundergraduatelevel. In this course,we systematically deals with singular homology and cohomology and Poicaréduality. Our goal was to give a pretty standard classical approach to these subjects. Moreover,we wanted tointroducestudentsto thebasiclanguagelofcategorytheoryandsimplicialsets,so usefulthroughoutmathematicsandfindingtheirfirstrealmanifestationsinalgebraictopology.we also wanted to stress the methods of homological algebra, for similar reasons. In order toprove the Poincare duality, we systematically discuss the relative cap product and Cechcohomology. 课程目标与内容(Courseobjectivesandcontents) *课程目标 (CourseObject) 1.要求学生掌握同调和上同调的概念、以及基本计算方法。(A3,B1) 2.要求学生理解范畴理论和单纯集的基本语言。(A3,B1,B3) 3.要求学生理解庞加莱对偶的证明,并且能够利用庞加莱对偶处理一些问题。(A3,B2,C1) *教学内容进度 安排及对应课 程目标(Class Schedule &Requirements &CourseObjecti ves) 章节 教学内 容(要 点) 教学目标 学时 教学形式 作业及考 核要求 课程思政融入 点 对应课程目 标 第 一 章 奇异同 调(计 13 小 节) 1. 掌握同 调和上 同调的 概念、基 本理论。 2. 学会利 用函子 的自然 性研究 问题 20 面授 习题 通过课埻教学 与课后作业培 养学生一丝不 苟、认真严谨 的科学态度。 A3,B1,B2
1. 常握利 用C复开 计算同 十算 和上同 调和」 通过课垃教学 同调的 的方法 与课后作培 章握万 16 习 东学生 的方法 丝不A3,B1,B2 、认真严谨 (计12 的科学态度 小节) 3 Kuneth 公式 理解庞加 偶定理的 第三章 (计证明,并且 3,B1,B3 够利用其处 6小节) 认 理一些习题 与问题 的科学态 考核方式 (1)平时作业50分 (Grading) (2)期末考试50分 必含信息:敕材名称作者,出板社,出版年份,板次。书号) LecturesonAlgebraicTopology.HaynesMiller(MIT).Fall2016 料(Te AllenHatcher. AlgebraicTopology CambridgeUniversityPress,2002 erials) 其它(More) 备注(Notes) 备注说明: 1.带内容为必填项 课程简介字数为30-500字;课程大纲以表述清楚教学安排为宜,字数不限
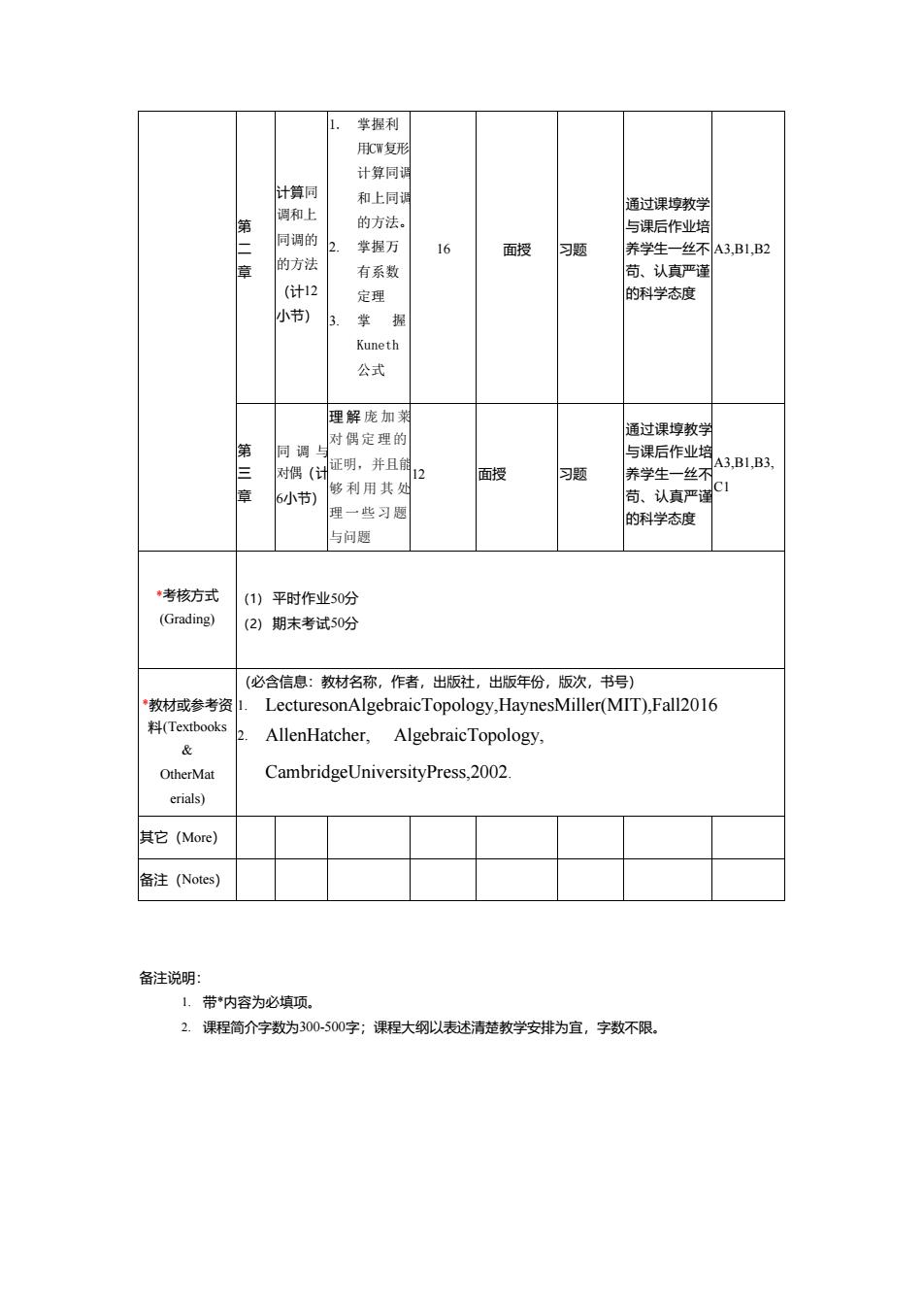
第 二 章 计算同 调和上 同调的 的方法 (计12 小节) 1. 掌握利 用CW复形 计算同调 和上同调 的方法。 2. 掌握万 有系数 定理 3. 掌 握 Kuneth 公式 16 面授 习题 通过课埻教学 与课后作业培 养学生一丝不 苟、认真严谨 的科学态度 A3,B1,B2 第 三 章 同调与 对偶(计 6小节) 理 解 庞加莱 对偶定理的 证明,并且能 够利用其处 理一些习题 与问题 12 面授 习题 通过课埻教学 与课后作业培 养学生一丝不 苟、认真严谨 的科学态度 A3,B1,B3, C1 *考核方式 (Grading) (1) 平时作业50分 (2) 期末考试50分 *教材或参考资 料(Textbooks & OtherMat erials) (必含信息:教材名称,作者,出版社,出版年份,版次,书号) 1. LecturesonAlgebraicTopology,HaynesMiller(MIT),Fall2016 2. AllenHatcher, AlgebraicTopology, CambridgeUniversityPress,2002. 其它(More) 备注(Notes) 备注说明: 1. 带*内容为必填项。 2. 课程简介字数为300-500字;课程大纲以表述清楚教学安排为宜,字数不限