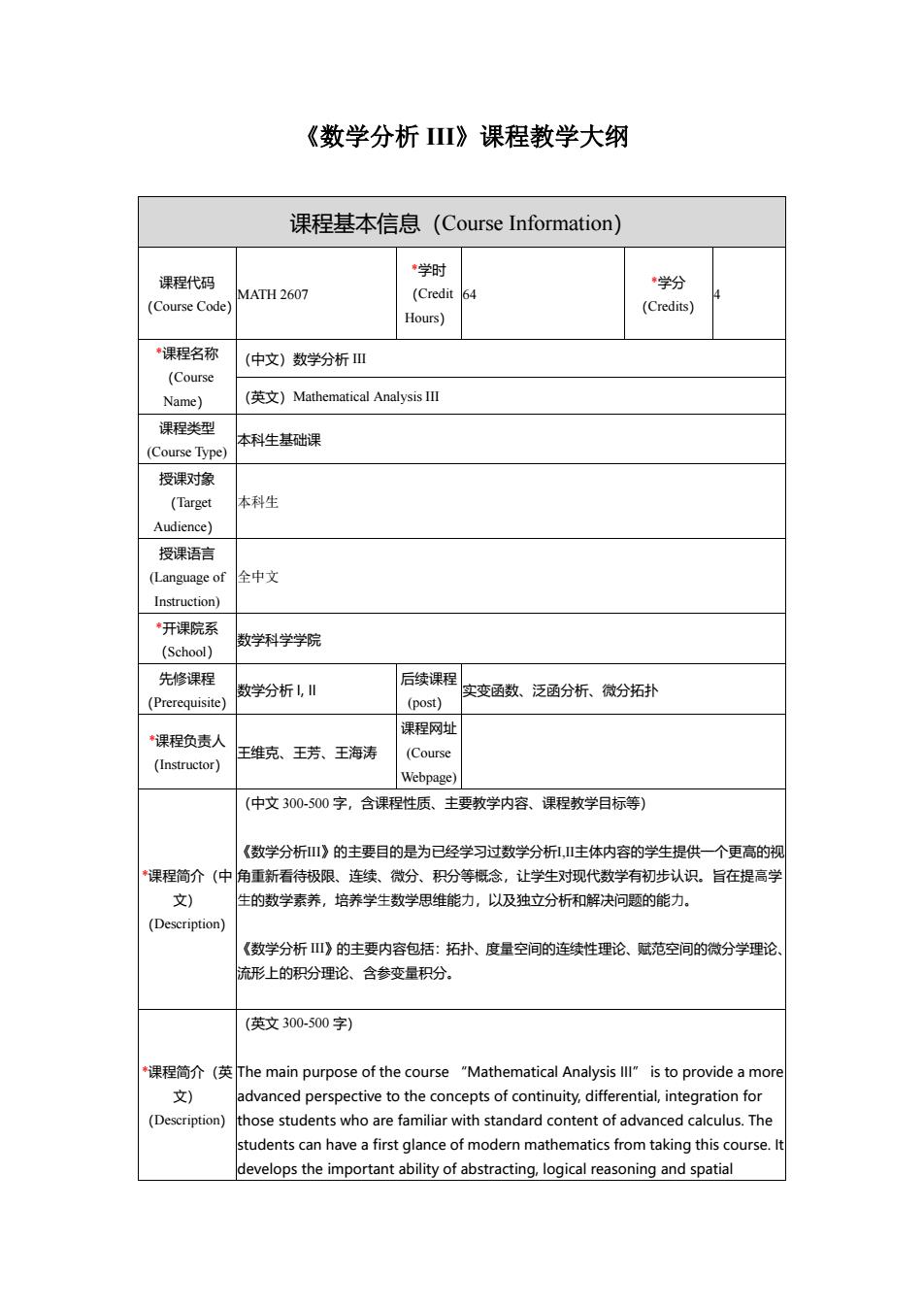
《数学分析Ⅲ》课程教学大纲 课程基本信息(Course Information) 课程代码 学时 MATH 2607 4 学纷 (CourseC Hours) (Credits) 课程名称 (中文)数学分析Ⅲ (Course Name) ('英文)Mathematical Analysis III 课程类型 本科生基础课 (Course Type 授课对家 (Target 本科生 Audience) 授课语言 ((Langunge of全中文 Instruction) “开课院系 数学科学学院 (School) 先修课程 (Prerequisite) 数学分析1,Ⅱ 后续课程实变函数泛通分折、微分拓扑 (nost) *课程负责人 课程网址 王维克、王芳、王海涛 (Course (Instructor) Webpage) (中文300-500字,含课程性质、主要教学内容、课程教学目标等) 《数学分析)的主要目的是为已经学习过数学分析,主体内容的学生提供一个更高的 *课程简介(中角重新看待极限、连续、微分、积分等概念,让学生对现代数学有初步认识。旨在提高学 文) 生的数学素养,培养学生数学思维能力,以及独立分析和解决问题的能力。 (Description) 《数学分析)的主要内容包括:拓扑、度量空间的连续性理论、赋范空间的微分学理论 形上的积分理论、含参变量积盼。 (英文300-500字) 课程简介(英The main purpose of the course"Mathematical Anaysis is to provide amo 文) advanced perspective to the concepts of continuity,differential,integration for (Description)those students who are familiar with standard content of advanced calculus.The students can have a first glance of modern mathematics from taking this course.I develops the important ability of abstracting,logical reasoning and spatial
《数学分析 III》课程教学大纲 课程基本信息(Course Information) 课程代码 (Course Code) MATH 2607 *学时 (Credit Hours) 64 *学分 (Credits) 4 *课程名称 (Course Name) (中文)数学分析 III (英文)Mathematical Analysis III 课程类型 (Course Type) 本科生基础课 授课对象 (Target Audience) 本科生 授课语言 (Language of Instruction) 全中文 *开课院系 (School) 数学科学学院 先修课程 (Prerequisite) 数学分析 I, II 后续课程 (post) 实变函数、泛函分析、微分拓扑 *课程负责人 (Instructor) 王维克、王芳、王海涛 课程网址 (Course Webpage) *课程简介(中 文) (Description) (中文 300-500 字,含课程性质、主要教学内容、课程教学目标等) 《数学分析III》的主要目的是为已经学习过数学分析I,II主体内容的学生提供一个更高的视 角重新看待极限、连续、微分、积分等概念,让学生对现代数学有初步认识。旨在提⾼学 ⽣的数学素养,培养学⽣数学思维能⼒,以及独立分析和解决问题的能⼒。 《数学分析 III》的主要内容包括:拓扑、度量空间的连续性理论、赋范空间的微分学理论、 流形上的积分理论、含参变量积分。 *课程简介(英 文) (Description) (英文 300-500 字) The main purpose of the course “Mathematical Analysis III” is to provide a more advanced perspective to the concepts of continuity, differential, integration for those students who are familiar with standard content of advanced calculus. The students can have a first glance of modern mathematics from taking this course. It develops the important ability of abstracting, logical reasoning and spatial
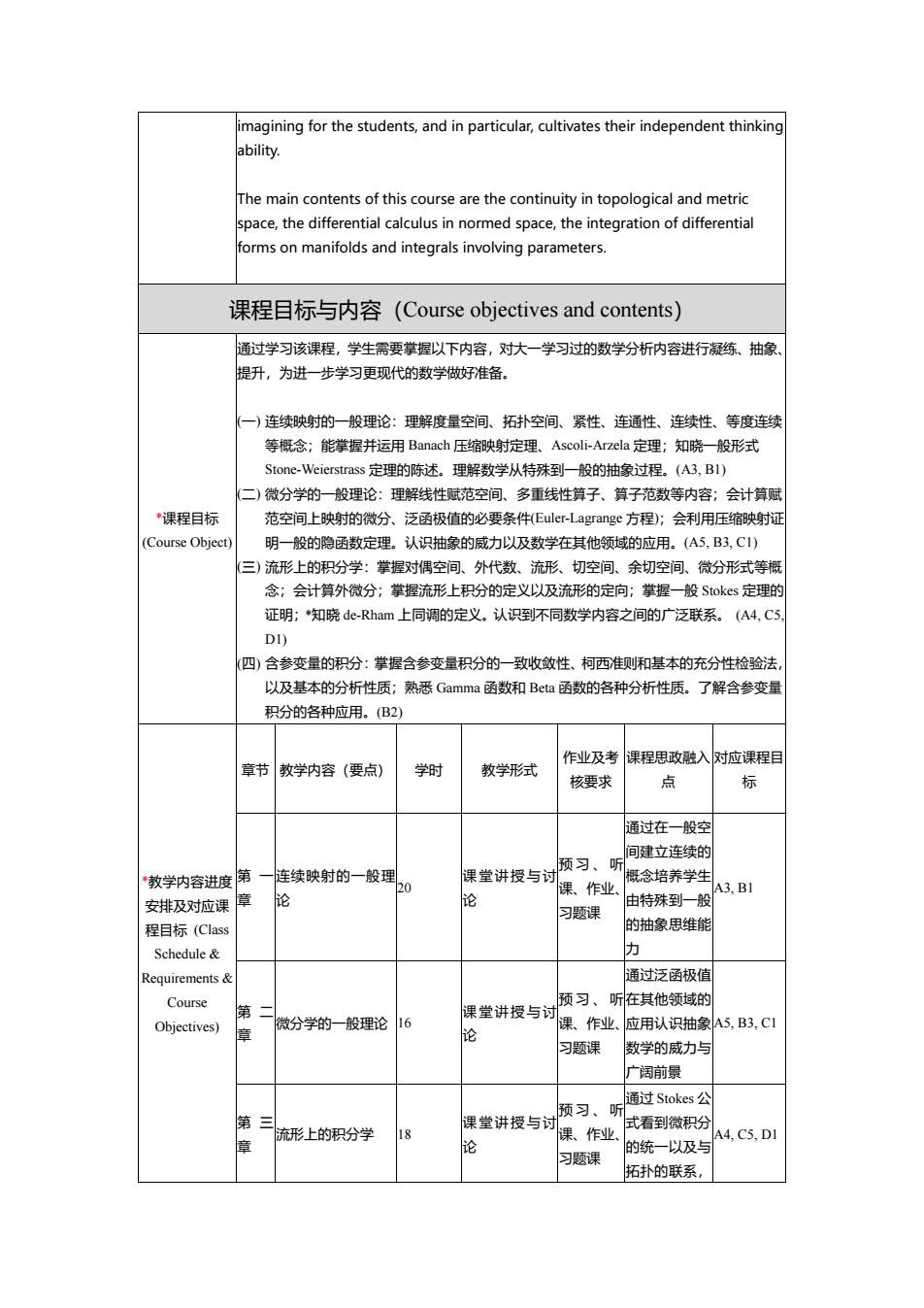
imagining for the students,and in particular,cultivates their independent thinking The main contents of this course are the continuity in topological and metric space,the differential calculus in normed space.the integration of differential forms on manifolds and integrals involving parameters. 课程目标与内容(Course objectives and contents) 通过学习该课程,学生需要掌握以下内容,对大一学习过的数学分析内容进行凝练、抽象, 提升,为进一步学习更现代的数学做好准备 一)连续映射的一般理论:理解度量空间、拓扑空间、紧性、连通性、连续性、等度连续 等概念:能掌据并运用Banach压缩映射定理、Ascoli-Arzela定理:知晓一般形式 tone-Weierstrass定理的陈沫。理银款学从特殊到一铅的抽象寸程.(A3.B1) 微分学的一般理论:理解线性范空间多重线性算子、算子范数等内容 :会计算 *课程目标 范空间上映射的微分.泛函极值的必要条件Euler,-Lagrange方程:会利用压缩映射远 (Course Object) 明一般的隐函数定理。认识抽象的威力以及数学在其他领域的应用。(A5,B3,C1) 三)流形上的积分学:掌握对偶空间、外代数、流形、切空间、余切空间、微分形式等概 念:会计算外微分:掌握流形上积分的定义以及流形的定向:掌握一般Soks定理的 证明:知晓dc-Ram上同调的定义.认识到不同数学内容之间的广泛联系,(4,C D (四)含参变量的积分:掌握含参变量积分的一致收敛性、柯西准则和基本的充分性检验法 以及基本的分析性质:熟悉Gamma函数和Beta函数的各种分析性质.。了解含参变量 积分的名种应用.(B2) 章节教学内容(要点) 学时 作业及考课程思政融入对应课程目 教学形式 核要求 通过在一般空 间建立连续 教学内容进度第 一连续映射的一般理 课堂讲授与讨顾习、听 慑念培养学丝 棵作业 A3,BI 安排及对应课 章 论 由结殊到一船 习题课 程目标(Cas 的抽象思维能 Schedule& Requirements 通过泛函极 Course 预习、听在其他领域的 第 课堂讲授与 微分学的一般理论 16 时课、作业,应用认识抽象A5B3,C1 习题课 广阔前 话过Stokes公 预习、 筑三 式看到微积 流形上的积分学 课堂讲授与讨 课、作业 A4.C5.D1 习题课 拓扑的联系
imagining for the students, and in particular, cultivates their independent thinking ability. The main contents of this course are the continuity in topological and metric space, the differential calculus in normed space, the integration of differential forms on manifolds and integrals involving parameters. 课程目标与内容(Course objectives and contents) *课程目标 (Course Object) 通过学习该课程,学生需要掌握以下内容,对大一学习过的数学分析内容进行凝练、抽象、 提升,为进一步学习更现代的数学做好准备。 (一) 连续映射的一般理论:理解度量空间、拓扑空间、紧性、连通性、连续性、等度连续 等概念;能掌握并运用 Banach 压缩映射定理、Ascoli-Arzela 定理;知晓一般形式 Stone-Weierstrass 定理的陈述。理解数学从特殊到一般的抽象过程。(A3, B1) (二) 微分学的一般理论:理解线性赋范空间、多重线性算子、算子范数等内容;会计算赋 范空间上映射的微分、泛函极值的必要条件(Euler-Lagrange 方程);会利用压缩映射证 明一般的隐函数定理。认识抽象的威力以及数学在其他领域的应用。(A5, B3, C1) (三) 流形上的积分学:掌握对偶空间、外代数、流形、切空间、余切空间、微分形式等概 念;会计算外微分;掌握流形上积分的定义以及流形的定向;掌握一般 Stokes 定理的 证明;*知晓 de-Rham 上同调的定义。认识到不同数学内容之间的广泛联系。 (A4, C5, D1) (四) 含参变量的积分:掌握含参变量积分的一致收敛性、柯西准则和基本的充分性检验法, 以及基本的分析性质;熟悉 Gamma 函数和 Beta 函数的各种分析性质。了解含参变量 积分的各种应用。(B2) *教学内容进度 安排及对应课 程目标 (Class Schedule & Requirements & Course Objectives) 章节 教学内容(要点) 学时 教学形式 作业及考 核要求 课程思政融入 点 对应课程目 标 第 一 章 连续映射的一般理 论 20 课堂讲授与讨 论 预习、听 课、作业、 习题课 通过在一般空 间建立连续的 概念培养学生 由特殊到一般 的抽象思维能 力 A3, B1 第 二 章 微分学的一般理论 16 课堂讲授与讨 论 预习、听 课、作业、 习题课 通过泛函极值 在其他领域的 应用认识抽象 数学的威力与 广阔前景 A5, B3, C1 第 三 章 流形上的积分学 18 课堂讲授与讨 论 预习、听 课、作业、 习题课 通过 Stokes 公 式看到微积分 的统一以及与 拓扑的联系, A4, C5, D1

认识到数学的 统性 在工程、物理 预习、听问题中通过驻 第四 课堂讲授与讨 含参变量的积分 10 课、作业、点法求渐近行B2,B3 习理 为。理论联系 实际 注1:建议按照教学周周学时编排. 注2:相应章节的课程思政融入点根据实际情况填写。 (11平时作业20分 考核方式 (2)期中考试30分 (Grading) (3)期末考试30分 (4)课程小论文10分 教材:数学分析(第二卷)(第7版),BA卓里奇著,李植译,高等教育出版社 敏材成参考格 Other 1)数学分析讲义,陈天权,北凉大学出版社 Materials) 2)数学分析原理,Walter Rudin,机械工业出版社 高等微积分,Lynn H.Loomis,Shlomo Stemberg,高等教育出版社 其它(More) 备注(Notes) 备注说明: 1.带*内容为必填项。 2.课程简介字数为300500字:课程大纲以表述清菀教学安排为宜,字数不限
认识到数学的 统一性 第 四 章 含参变量的积分 10 课堂讲授与讨 论 预习、听 课、作业、 习题课 在工程、物理 问题中通过驻 点法求渐近行 为,理论联系 实际 B2, B3 注 1:建议按照教学周周学时编排。 注 2:相应章节的课程思政融入点根据实际情况填写。 *考核方式 (Grading) (1)平时作业 20 分 (2)期中考试 30 分 (3)期末考试 30 分 (4)课程小论文 10 分 *教材或参考资 料 (Textbooks & Other Materials) 教材:数学分析(第二卷)(第 7 版),B.A. 卓里奇 著,李植 译, 高等教育出版社 参考书: 1)数学分析讲义,陈天权,北京大学出版社 2)数学分析原理,Walter Rudin,机械工业出版社 高等微积分,Lynn H.Loomis, Shlomo Sternberg,高等教育出版社 其它(More) 备注(Notes) 备注说明: 1.带*内容为必填项。 2.课程简介字数为 300-500 字;课程大纲以表述清楚教学安排为宜,字数不限