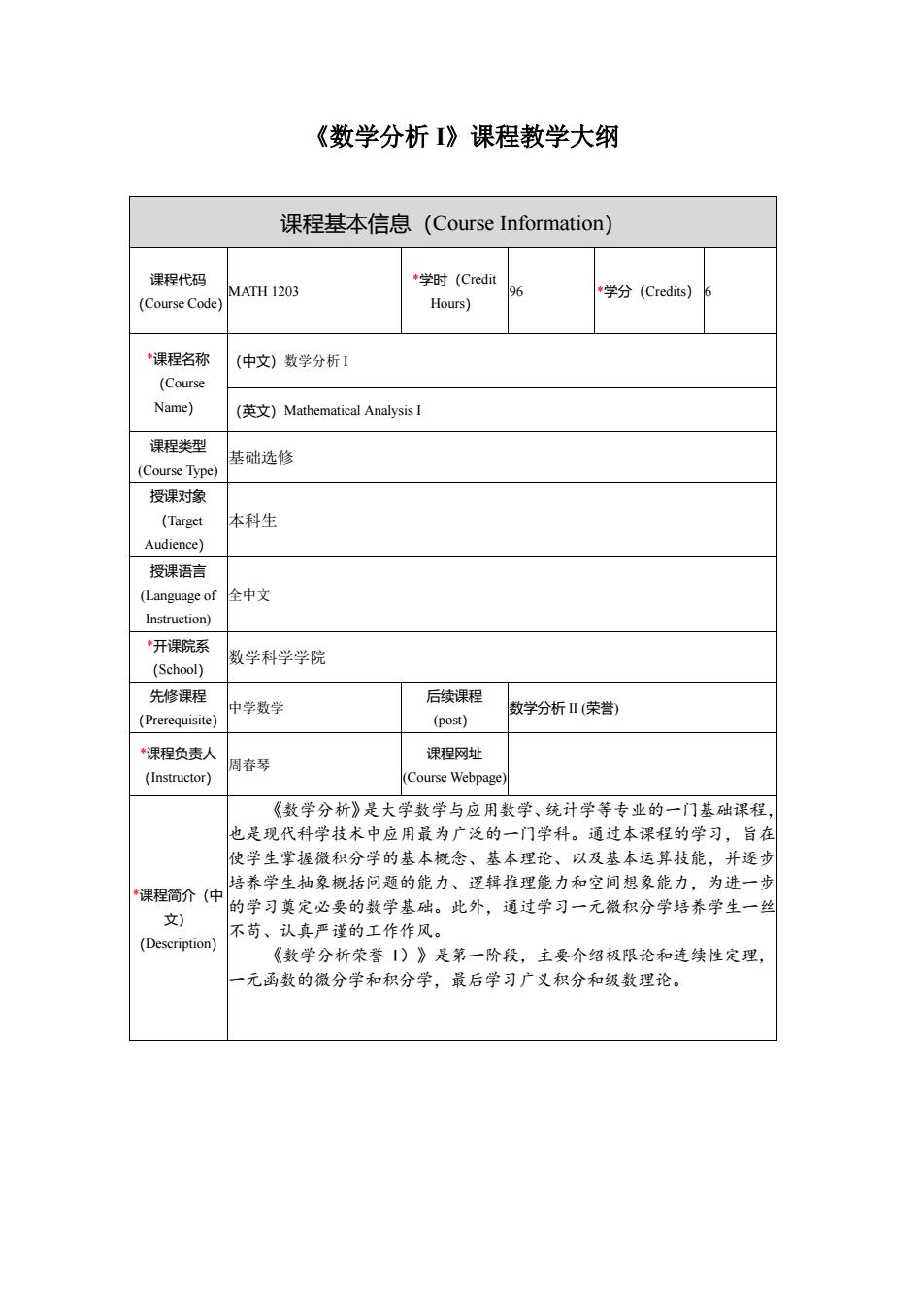
《数学分析I》课程教学大纲 课程基本信息(Course Information) 课程代码 MATH 1203 *学时(Credit 96 学分(Credits)6 Course Code) Hours) 课程名称 (中文)数学分析】 (Co Name) (英文)Mathematical AnalysisI 课程类型 (Course Type) 基础选修 授课对象 (Target 本体科生 Audience) 授课语言 (Language of 全中文 Instruction) 开课院系 数学科学学院 先修课程 中学数学 后续课程 学分析Ⅱ(荣誉) (Prerequisite) (post) “课程负责人 周春琴 课程网址 (Instructor) (Course Webpage 《数学分析》是大学数学与应用数学、统计学等专业的一门基础课程 也是现代科学技术中应用最为广泛的一门学科。通过本课程的学习,旨在 使堂生堂据微积分学的基本都余、基本理论、以及基本运算技能、并源出 培养学生抽象概括问题的能力、逻辑推理能力和空间想象能力, 为进 课程简介(仲的学习莫定必要的数学基础。此外,通过学习一无微积分学培养学生一丝 文) (Description) 不苟、认真严谨的工作作风。 《数学分析荣誉)》是第一阶段,主要介绍极限论和连续性定理, 一元函数的微分学和积分学,最后学习广义积分和级数理论
《数学分析 I》课程教学大纲 课程基本信息(Course Information) 课程代码 (Course Code) MATH 1203 *学时(Credit Hours) 96 *学分(Credits) 6 *课程名称 (Course Name) (中文)数学分析 I (英文)Mathematical Analysis I 课程类型 (Course Type) 基础选修 授课对象 (Target Audience) 本科生 授课语言 (Language of Instruction) 全中文 *开课院系 (School) 数学科学学院 先修课程 (Prerequisite) 中学数学 后续课程 (post) 数学分析 II (荣誉) *课程负责人 (Instructor) 周春琴 课程网址 (Course Webpage) *课程简介(中 文) (Description) 《数学分析》是大学数学与应用数学、统计学等专业的一门基础课程, 也是现代科学技术中应用最为广泛的一门学科。通过本课程的学习,旨在 使学生掌握微积分学的基本概念、基本理论、以及基本运算技能,并逐步 培养学生抽象概括问题的能力、逻辑推理能力和空间想象能力,为进一步 的学习奠定必要的数学基础。此外,通过学习一元微积分学培养学生一丝 不苟、认真严谨的工作作风。 《数学分析荣誉 I)》是第一阶段,主要介绍极限论和连续性定理, 一元函数的微分学和积分学,最后学习广义积分和级数理论
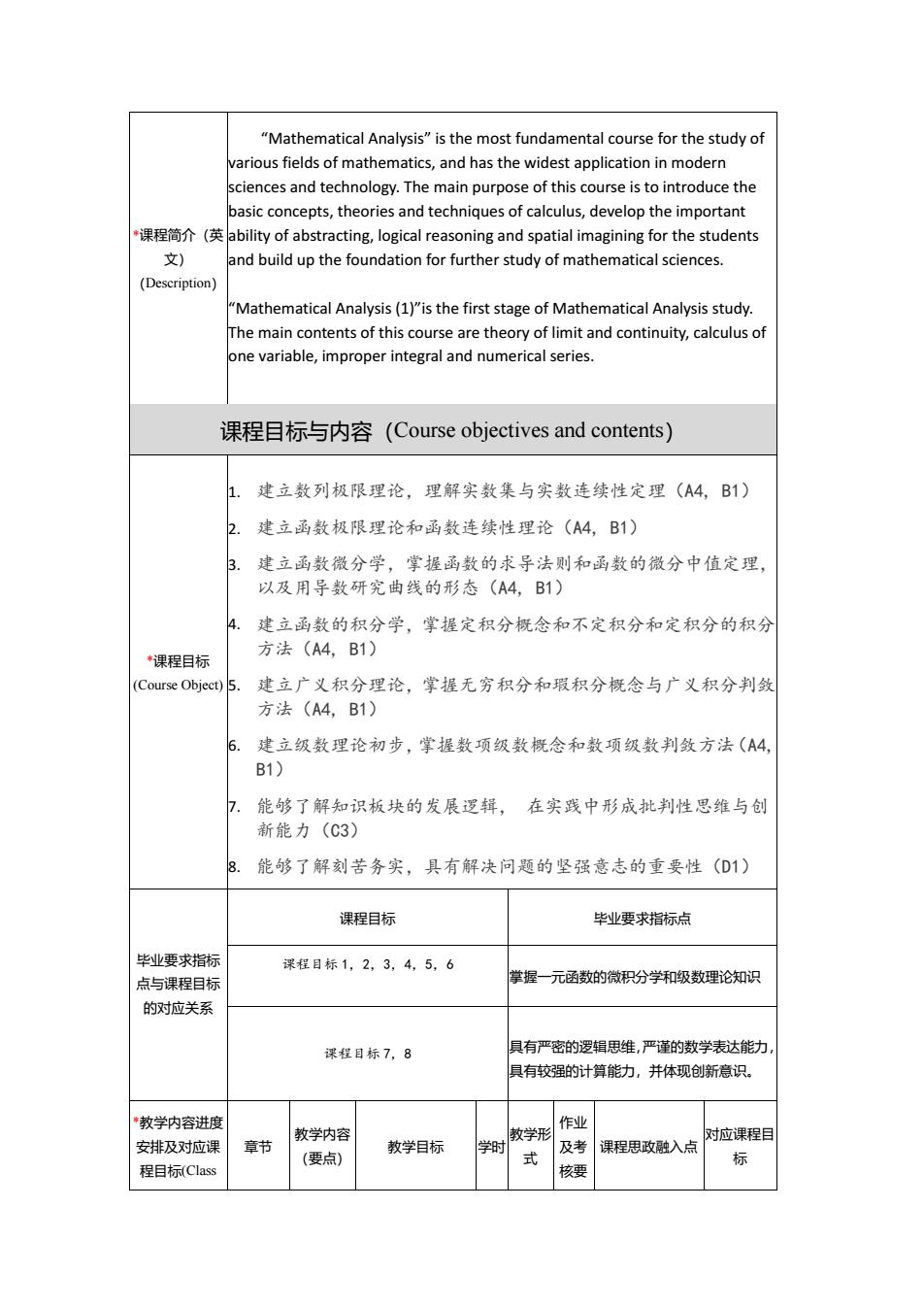
"Mathematical Analysis"is the most fundamental course for the study of arious fields of mathematics,and has the widest application in mode sciences and technology.The main purpose of this course is to introduce the basic concepts,theories and techniques of calculus.develop the important “课程简介(英ability of abstracting,logical reasoning and spatial imagining for the students 文) and build up the foundation for further study of mathematical sciences. cription) "Mathematical Analysis(1)"is the first stage of Mathematical Analysis study. The main contents of this course are theory of limit and continuity,calculus of one variable,improper integral and numerical series. 课程目标与内容(Course objectives and contents) 1 建立数列极限理论,理解实数集与实数连续性定理(A4,B1) 2.建立函数极限理论和函数连续性理论(A4,B1) 3. 建立函数微分学,掌握函数的求导法则和函数的微分中值定理, 以及用导数研究曲线的形态(A4,B1) 4. 建立函数的积分学,掌握定积分概念和不定积分和定积分的积分 课程目标 方法(A4,B1) Course Object)5. 建立广义积分理论,掌握无穷积分和瑕积分概念与广义积分判敛 方法(A4,B1) 6. 建立级数理论初步,掌提数项级数概念和数项级数判敛方法(4 B1) 能够了解知识板块的发展逻辑, 在实践中形成批判性思维与创 新能力(C3) 8.能够了解刻苦务实,具有解决问题的坚强意志的重要性(D1) 课程目标 毕业要求指标点 毕业要求指标 课往目标1,2,3,4,5,6 点与课程目板 学握一元函数的微积分学和级数理论知识 的对应关系 课程目标7,8 具有严的逻辑思维,严谨的数学表达能力 有较强的计号 能力,并体现创新意识 教学内容讲度 作业 安排及对应课 章节 教学内容 对应课程目 (要点) 教学目标 及考课程思改融入点} 标 程目标Clas 核瘦
*课程简介(英 文) (Description) “Mathematical Analysis” is the most fundamental course for the study of various fields of mathematics, and has the widest application in modern sciences and technology. The main purpose of this course is to introduce the basic concepts, theories and techniques of calculus, develop the important ability of abstracting, logical reasoning and spatial imagining for the students and build up the foundation for further study of mathematical sciences. “Mathematical Analysis (1)”is the first stage of Mathematical Analysis study. The main contents of this course are theory of limit and continuity, calculus of one variable, improper integral and numerical series. 课程目标与内容(Course objectives and contents) *课程目标 (Course Object) 1. 建立数列极限理论,理解实数集与实数连续性定理(A4, B1) 2. 建立函数极限理论和函数连续性理论(A4, B1) 3. 建立函数微分学,掌握函数的求导法则和函数的微分中值定理, 以及用导数研究曲线的形态(A4, B1) 4. 建立函数的积分学,掌握定积分概念和不定积分和定积分的积分 方法(A4, B1) 5. 建立广义积分理论,掌握无穷积分和瑕积分概念与广义积分判敛 方法(A4, B1) 6. 建立级数理论初步,掌握数项级数概念和数项级数判敛方法(A4, B1) 7. 能够了解知识板块的发展逻辑, 在实践中形成批判性思维与创 新能力(C3) 8. 能够了解刻苦务实,具有解决问题的坚强意志的重要性(D1) 毕业要求指标 点与课程目标 的对应关系 课程目标 毕业要求指标点 课程目标 1,2,3,4,5,6 掌握一元函数的微积分学和级数理论知识 课程目标 7,8 具有严密的逻辑思维,严谨的数学表达能力, 具有较强的计算能力,并体现创新意识。 *教学内容进度 安排及对应课 程目标(Class 章节 教学内容 (要点) 教学目标 学时 教学形 式 作业 及考 核要 课程思政融入点 对应课程目 标

Schedule& 求 Course Objectives) 微积分的其 本思想和内容 通过学习实数 第一章 装合的基本 堂深后1培养学生 1,B1, 堵论 念,实数的引进 讲解作业 -丝不苟、认真63,D1 映好射的宝义妇 严谨的工作作 一对应撒金 数列极限概念 性质,子列概念 单调有界收敛京 数列机 理.Cauchv收 第二章 限与实 学科知识 A1,B1 *闲区间套定 讲解作业 理,*有界数列有 收敛子列定理, 确累与骆界原理 函数的概念与性 禹数极限 念,函数极限妆 敛定理,函数树 限计算,无穷 数 第三章 限与 函数连续 讲解 作业 学科知识 与 函数的 连续性。闭区间 上连续函数的: 第四草 元 分学 作业 解决问题 微分中值定理 导数的应用 不定积分概念 第一换元积分 第二换元积 第五章 ·元积 分法,分部积分 2 课堂保后引 A1,B1, 分学 讲授作业 解决问题 C3,D1 无理数的积
Schedule & Requirements & Course Objectives) 求 第一章 绪论 介绍微积分的基 本思想和内容, 集 合 的 基 本 概 念,实数的引进, 映射的定义和一 一对应概念 4 课 堂 讲解 课 后 作业 通过学习实数 引进培养学生 一丝不苟、认真 严谨的工作作 风 A1,B1, C3,D1 第二章 数 列 极 限 与 实 数 基 本 定理 数列极限概念与 性质,子列概念, 单调有界收敛定 理,Cauchy 收敛 准则,Stolz 定 理,*闭区间套定 理,*有界数列有 收敛子列定理,* 确界与确界原理 12 课 堂 讲解 课 后 作业 学科知识 A1,B1, C3,D1 第三章 函 数 极 限 与 连 续 函数的概念与性 质,函数极限概 念,函数极限收 敛定理,函数极 限计算,无穷小 量与无穷大量, 函 数 连 续 与 间 断,函数的一致 连续性,闭区间 上连续函数的性 质 18 课 堂 讲解 课 后 作业 学科知识 A1,B1, C3,D1 第四章 一 元 微 分学 导 数 与 微 分 概 念,求导法则与 导数计算,微分 和导数的简单应 用,高阶导数, 微分中值定理; 导数的应用 20 课 堂 讲授 课 后 作业 解决问题 A1,B1, C3,D1 第五章 一 元 积 分学 不定积分概念, 第 一 换 元 积 分 法,第二换元积 分法,分部积分 法,三角函数、 有理函数和简单 无 理 函 数 的 积 22 课 堂 讲授 课 后 作业 解决问题 A1,B1, C3,D1

分,定积分概念」 可积性理论,常 见可可积函数美 应用 义积分收敛与 发散概念 auchy收经f 则,绝对收敛与 广义积 课误后 A1 B1 第六章 生 讲授作业 创新思维 积分与環积分 c3,1 敛法,广义积分 的计算 级数的收与发 收概念 数的性质,上 极限,Cauch 收敛准则,正项 七章 数项 讲授 系统思维 作亚 敛法,任意项 散的判敛法,绝 对收敛与条件是 数级数的性质 Cauchy来 (1)平时作业20分 考核方式 (2)三次测验共45分 (Grading) (3)期末考试35分 《数学分析》陈纪修等编, 高等教有出版社 参考书: 《数学分析教程》常庚哲等编,中国科学技术大学出版科 教材或参考泾 《数学分析》徐森林等编,清华大学出版社 《微积分学教程》菲赫金哥尔茨等编,高等教育出版社 料HTexthooks& ther Materials)) 《数学分析》卓里奇编,蒋锋等译,高等教有出版社 《数学分析原理》Wal Rudin 机械工业出版社 《数学分析学习指导书》吴良森等编, 高等教有出版社 《数学分析学习指导》表兆泰等编,科学出版社
分,定积分概念, 可积性理论,常 见可积函数类, 定 积 分 基 本 性 质,变上限函数, Newton-Leibniz 公式,积分第二 中值定理,定积 分的几何与物理 应用 第六章 广 义 积 分 广义积分收敛与 发散概念, Cauchy 收 敛 准 则,绝对收敛与 条件收敛,无穷 积分与瑕积分判 敛法,广义积分 的计算 8 课 堂 讲授 课 后 作业 创新思维 A1,B1, C3,D1 第七章 数 项 级 数 级数的收敛与发 散概念,收敛级 数的性质,上下 极限, Cauchy 收敛准则, 正项 级 数 的 判 敛 方 法,交错级数判 敛法,任意项级 数的判敛法,绝 对收敛与条件收 敛级数的性质, Cauchy 乘积 12 课 堂 讲授 课 后 作业 系统思维 A1,B1, C3,D1 *考核方式 (Grading) (1)平时作业 20 分 (2)三次测验共 45 分 (3)期末考试 35 分 *教材或参考资 料(Textbooks & Other Materials) 教材: 《数学分析》陈纪修等编,高等教育出版社 参考书:《数学分析教程》常庚哲等编,中国科学技术大学出版社 《数学分析》徐森林等编,清华大学出版社 《微积分学教程》菲赫金哥尔茨等编,高等教育出版社 《数学分析》卓里奇编,蒋铎等译,高等教育出版社 《数学分析原理》Walter Rudin 编,机械工业出版社 《数学分析学习指导书》吴良森等编,高等教育出版社 《数学分析学习指导》裘兆泰等编,科学出版社

其它(More) 备注(Nofes) 备注说明: 1.带内容为必填项。 2.课程简介字数为300-500字:课程大纲以表述清楚牧学安排为宜,字数不限
其它(More) 备注(Notes) 备注说明: 1.带*内容为必填项。 2.课程简介字数为 300-500 字;课程大纲以表述清楚教学安排为宜,字数不限