《高等数学》课程教学大纲 课程基本信息(Course Information) 课程代码 *学时 MATHI201 学分 Hours) *课程名称 (中文)高等数学1 (Course Name】 (英文)Calculus 课程类型 (Course Type) 必修课 授课对象 (Target 本科生 Audience) 授课语言 (Language of 全中文 Instruction) 数学学院 先修课程 无 (Prerequisite) 后续课程高等数学山 (nost) *课程负责人 课程网址 (Course http://math.sjtu.edu.cn/course/gskc/ (Instructor) Webpage) (中文300500字含里程性质丰要学内容里程学目标等) 《高等数学》课程是在现代科学技术、经济管理和人文科学等学科中应用最广泛的 门课程,是理工类高等院校非数学专业学生必修的一门重要基础理论课,也是培养造 层次专门人才所需数学知识与数学素养的基本课程,对于树立良好的学习习惯和学习动力 提高创新能力与综合素质起着极为重要的作用。课程不但为学生学习后续数学课程和其他 理工专业课程莫定必要的数学基础,而且对学生在数学的抽象性、逻辑性与严密性方面进 课程简介(中 行一定的训练和熏陶,使他们具有理解和运用逻辑关系、研究和领会抽象事物、认识和不 用数形规律的初步能力, 文) (Description) 通过本课程的学习,使学生获得有关连续变量的数学基本概念、基本理论和基本运算 方法,从而为各种后继课程的学习莫定必要的数学基础:另一方面培养学生抽象思维、远 辑推理、空间想象的能力,张化学生合理运用数学知识分析并解决实际问思的能力。 本门课程主要包括以下内容,函数、极限与连续、导数与微分、微分中值定理与导到 用 不定积分与定积分、常微分方程、向量代数与空间解析几何等几大板块
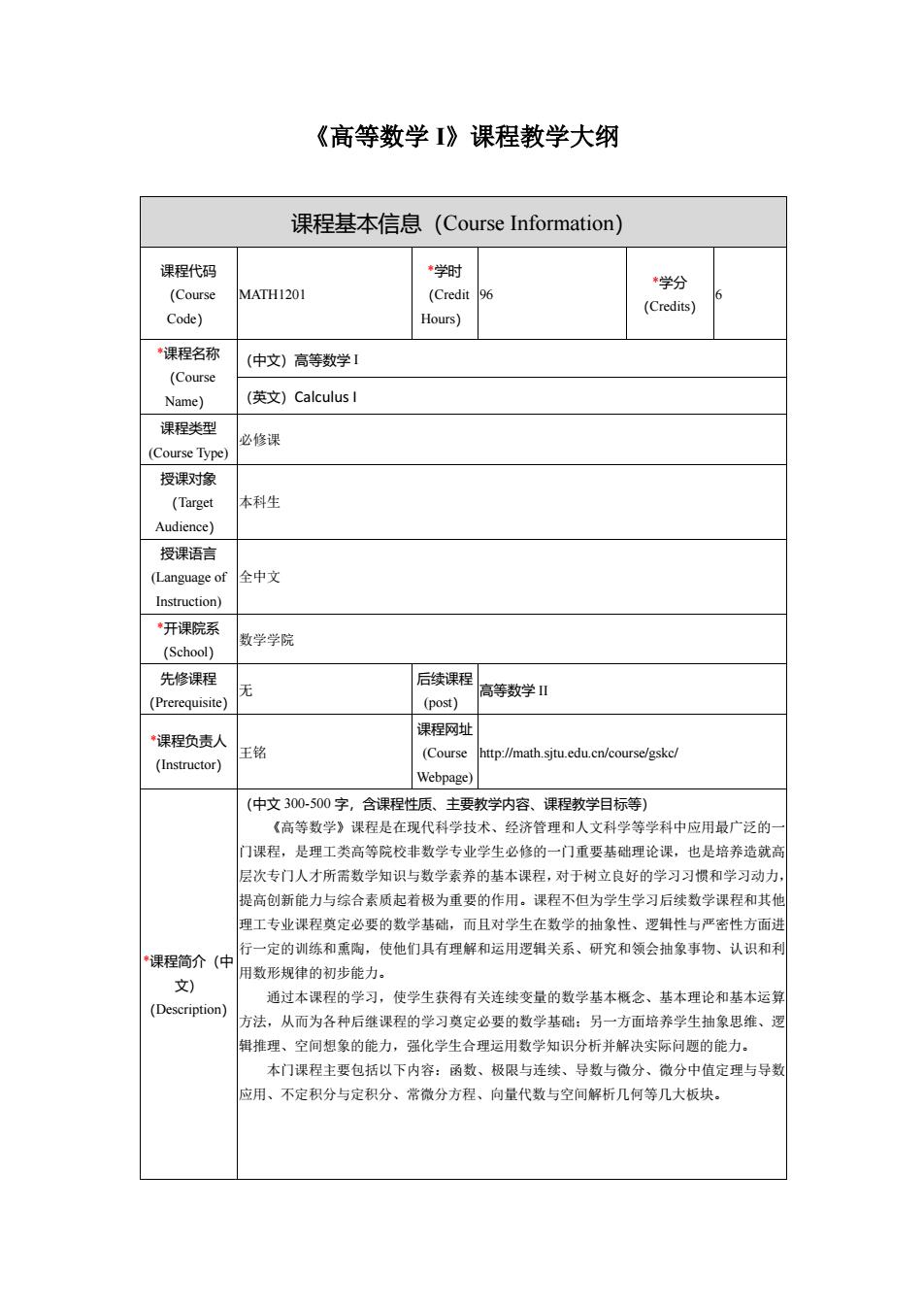
《高等数学 I》课程教学大纲 课程基本信息(Course Information) 课程代码 (Course Code) MATH1201 *学时 (Credit Hours) 96 *学分 (Credits) 6 *课程名称 (Course Name) (中文)高等数学 I (英文)Calculus I 课程类型 (Course Type) 必修课 授课对象 (Target Audience) 本科生 授课语言 (Language of Instruction) 全中文 *开课院系 (School) 数学学院 先修课程 (Prerequisite) 无 后续课程 (post) 高等数学 II *课程负责人 (Instructor) 王铭 课程网址 (Course Webpage) http://math.sjtu.edu.cn/course/gskc/ *课程简介(中 文) (Description) (中文 300-500 字,含课程性质、主要教学内容、课程教学目标等) 《高等数学》课程是在现代科学技术、经济管理和人文科学等学科中应用最广泛的一 门课程,是理工类高等院校非数学专业学生必修的一门重要基础理论课,也是培养造就高 层次专门人才所需数学知识与数学素养的基本课程,对于树立良好的学习习惯和学习动力, 提高创新能力与综合素质起着极为重要的作用。课程不但为学生学习后续数学课程和其他 理工专业课程奠定必要的数学基础,而且对学生在数学的抽象性、逻辑性与严密性方面进 行一定的训练和熏陶,使他们具有理解和运用逻辑关系、研究和领会抽象事物、认识和利 用数形规律的初步能力。 通过本课程的学习,使学生获得有关连续变量的数学基本概念、基本理论和基本运算 方法,从而为各种后继课程的学习奠定必要的数学基础;另一方面培养学生抽象思维、逻 辑推理、空间想象的能力,强化学生合理运用数学知识分析并解决实际问题的能力。 本门课程主要包括以下内容:函数、极限与连续、导数与微分、微分中值定理与导数 应用、不定积分与定积分、常微分方程、向量代数与空间解析几何等几大板块

Calculus is one of the most widely used theory in modern science and technology. majors in Colleges and universities of science and engineering.Also it is a basic cours for cultivating high-level professionals with mathematical knowledge and accomplishment. Calculus studying isone of the most efective ways for students to build up the go eaing habits and eing motivation Its plays a 文) This course provides not only necessary mathematical knowledge to follow-u (Description)Science and Engineering courses,but also proper training in mathematical abstractness logic and tightness.so as to foster students the preliminary ability to understand and apply the logic relationship,study and grasp the abstract recognize and use relationship between number and shape. The contents include Functions,Limits and Continuity,the Derivative,Integration. Differential equation,Vectors and Analytic Geometry. 课程目标与内容(Course objectives and contents) 结合本校办学定位、学生情况、专业人才培养要求,具体描述学习本课程后应该达到的知 识能九质价值水平 课程目标 ,获得有关连续变量的数学基本概念、基本理论和基本运算方法,从而为各种后继课程 的学习莫定必要的数学基础(A5): (Course Object) 2.培养抽象思堆、逻辑推理,空间想象的能力,强化合理运用数学知识分析并解决实际 问题的能力(B1,B2,C1,C2,C4)。 敏学内 章节 要 教学目标 学时 教学形式 作业及考课程思政融入对应课程 点) 核要求 点 标 教学内容进度 陪养学生具有 安排及对应课 扎实的基础理 程目标(Cas 论知识,具名 Schedule 了解数集,确 学习和应用知 课 Requirements Course 先修 函数性质, 6 课堂面授 Objectives) 参数方程不 思维与创新能 极坐标方程 力、终身学习 和自主学习能
*课程简介(英 文) (Description) Calculus is one of the most widely used theory in modern science and technology, economic management and humanities. It is a fundamental course for non mathematics majors in Colleges and universities of science and engineering. Also it is a basic course for cultivating high-level professionals with mathematical knowledge and accomplishment. Calculus studying is one of the most effective ways for students to build up the good learning habits and learning motivation. It also plays a critical role in training and improving students' innovation ability and integrated quality. This course provides not only necessary mathematical knowledge to follow-up Science and Engineering courses, but also proper training in mathematical abstractness, logic and tightness, so as to foster students the preliminary ability to understand and apply the logic relationship, study and grasp the abstract objects, recognize and use the relationship between number and shape. The contents include Functions, Limits and Continuity, the Derivative , Integration, Differential equation, Vectors and Analytic Geometry. 课程目标与内容(Course objectives and contents) *课程目标 (Course Object) 结合本校办学定位、学生情况、专业人才培养要求,具体描述学习本课程后应该达到的知 识、能力、素质、价值水平。 1. 获得有关连续变量的数学基本概念、基本理论和基本运算方法,从而为各种后继课程 的学习奠定必要的数学基础(A5); 2. 培养抽象思维、逻辑推理、空间想象的能力,强化合理运用数学知识分析并解决实际 问题的能力(B1,B2,C1,C2,C4)。 *教学内容进度 安排及对应课 程目标 (Class Schedule & Requirements & Course Objectives) 章节 教学内 容(要 点) 教学目标 学时 教学形式 作业及考 核要求 课程思政融入 点 对应课程目 标 第一 章 本课程 先修内 容 了解数集,确 界等概念,掌 握函数性质, 参数方程和 极坐标方程。 6 课堂面授 教材对应 习题 培养学生具有 扎实的基础理 论知识,具备 学习和应用知 识能力、适应 能力、批判性 思维与创新能 力、终身学习 和自主学习能 力 课程目标 1
培养学生具有 握极限 实的基础理 线的 论知识,具备 数列极 念,学捏 学习和应用: 穷小阶的传 识能力、话应 教材对应 课程目标 章 并用于计 14 课堂而授 能力、批判性 算极限。 维与创新能 0,2 解闭区间上 、终身学习 续函数的 和自主学习能 质 陪养学生具有 解导数 实的基础 义、可导性 论知识,具备 连续性的关 学习和应用知 导数, 分,高 系,熟练掌捏 识能力、适应 教材对应能力、批判性 课程目析 种函数 10 导数, 课堂面授 数应 形式的 习 思维与创新能 方法 了年 力、终身学习 常见导数 和自主学习能 用。 理解并热 掌握中值分 理:掌挥泰粉 培养学生具有 公式:熟练等 执实的基础现 握罗必塔》 论知识,具备 雨数极值和 学习和应用知 值定 识能力、适应 第四 导数 最值的计算 教材对因 课程目标 18 课堂面授 修力、批判性 音 去。孰线堂板 习题 1,2 究函马 思维与创新能 性态 数的单记 性和数图 力、终身学习 和自主学习能 形凹凸性 力 判别法:能角 快最值的成 用题:堂握不 等式的证明。 理解定积分 培养学生具有 的概念和基 扎实的基础理 定积分 第不定彩 本性质,掌损 教材对应论知识,具备课程目标 24 课堂面授 习题 学习和应用知,2 识能力、适应 能力九、批判性
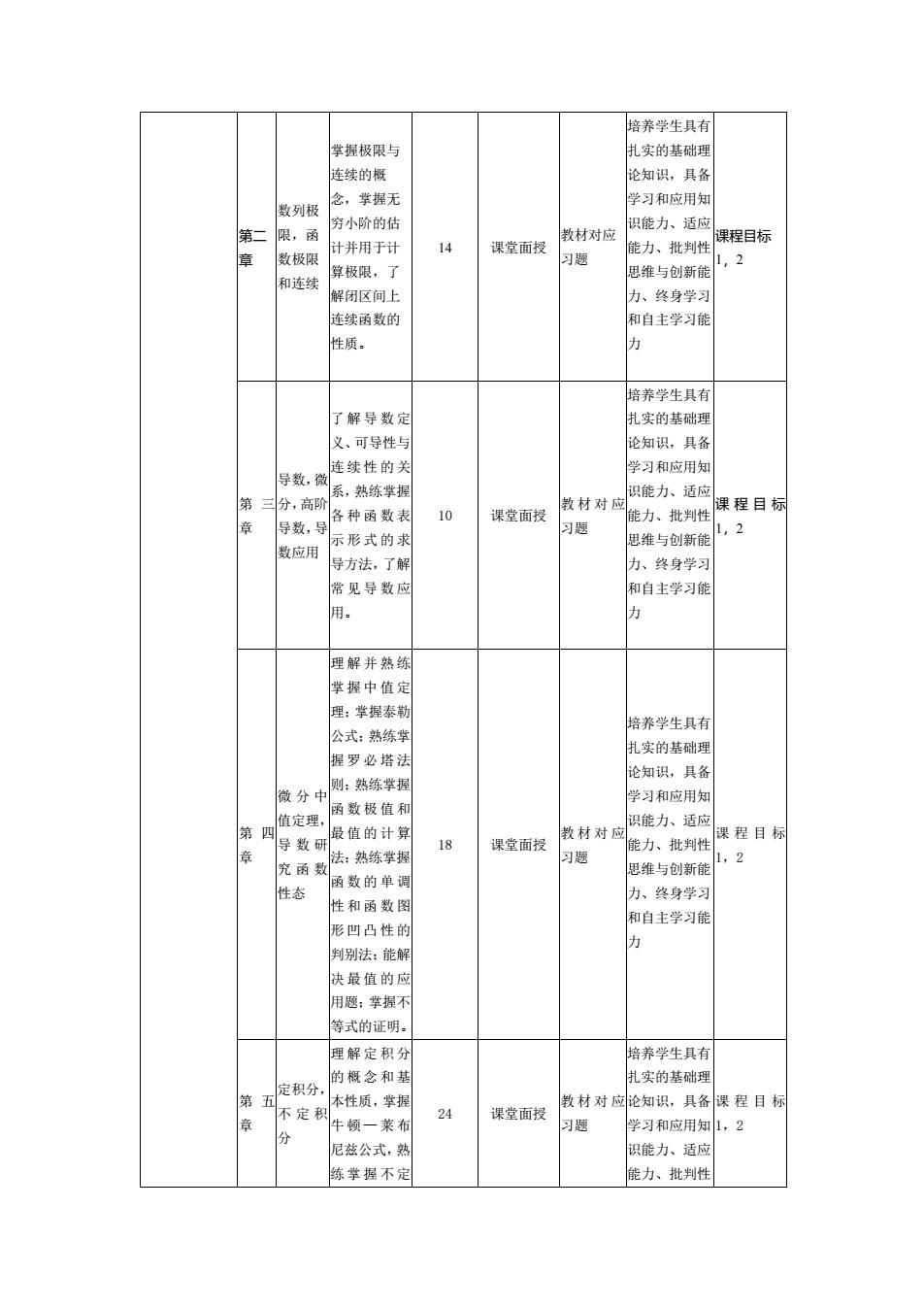
第二 章 数列极 限,函 数极限 和连续 掌握极限与 连续的概 念,掌握无 穷小阶的估 计并用于计 算极限,了 解闭区间上 连续函数的 性质。 14 课堂面授 教材对应 习题 培养学生具有 扎实的基础理 论知识,具备 学习和应用知 识能力、适应 能力、批判性 思维与创新能 力、终身学习 和自主学习能 力 课程目标 1,2 第 三 章 导数,微 分,高阶 导数,导 数应用 了解导数定 义、可导性与 连续性的关 系,熟练掌握 各种函数表 示形式的求 导方法,了解 常见导数应 用。 10 课堂面授 教材对应 习题 培养学生具有 扎实的基础理 论知识,具备 学习和应用知 识能力、适应 能力、批判性 思维与创新能 力、终身学习 和自主学习能 力 课程目标 1,2 第 四 章 微分中 值定理, 导数研 究函数 性态 理解并熟练 掌 握 中 值 定 理;掌握泰勒 公式;熟练掌 握罗必塔法 则;熟练掌握 函数极值和 最值的计算 法;熟练掌握 函数的单调 性和函数图 形凹凸性的 判别法;能解 决最值的应 用题;掌握不 等式的证明。 18 课堂面授 教材对应 习题 培养学生具有 扎实的基础理 论知识,具备 学习和应用知 识能力、适应 能力、批判性 思维与创新能 力、终身学习 和自主学习能 力 课程目标 1,2 第 五 章 定积分, 不定积 分 理解定积分 的概念和基 本性质,掌握 牛 顿 — 莱 布 尼兹公式,熟 练掌握不定 24 课堂面授 教材对应 习题 培养学生具有 扎实的基础理 论知识,具备 学习和应用知 识能力、适应 能力、批判性 课程目标 1,2

积分的换可 维与剑新能 法和分部积 九、锋身学 分法,定积 和自主学习能 的换元法利 分部积分法 堂据微元 积分应用。 了解微分方 程的相关概 培养学生具有 念,掌握常见 扎实的基础理 阶方程 法 理解 论知识。具名 学习和应用 常微 性方程解日 识能力、适应 结构理论:考 教材对园 课程目 方程或 12 握二阶线性 课堂而授 能力、批判性 习避 1,2 解简介 思维与创新能 程的 解法:握某 力、终身学习 特殊菲 和自主学习能 力 饮项的二 常系数线竹 方程的解法」 迎解向量日 定义,握 量运算性 及几何意义 培养学生具右 热练草可 用实的基础理 和直线的 论知识 具备 量行 冬型方程,熟 学习和应用: 识能力、适应 第七数,空间 解析厂 练掌握点、直 教材对因 课程目标 12 课堂而授 能力、批性 音 1,2 、平面之 思维与创新能 、终身学 立置关系的 和自主学习能 力 到断法:知道 标准二次曲 了解投 柱面和投是 曲线
积分的换元 法和分部积 分法,定积分 的换元法和 分部积分法, 掌握微元法 与积分应用。 思维与创新能 力、终身学习 和自主学习能 力 第 六 章 常微分 方程求 解简介 了解微分方 程 的 相 关 概 念,掌握常见 一阶方程的 解法;理解线 性方程解的 结构理论;掌 握二阶线性 方程的一般 解法;掌握某 些特殊非齐 次项的二阶 常系数线性 方程的解法。 12 课堂面授 教材对应 习题 培养学生具有 扎实的基础理 论知识,具备 学习和应用知 识能力、适应 能力、批判性 思维与创新能 力、终身学习 和自主学习能 力 课程目标 1,2 第 七 章 向量代 数,空间 解析几 何 理解向量的 定义,掌握向 量 运算性质 及几何意义。 熟练掌握平 面和直线的 各型方程,熟 练掌握点、直 线、平面之间 位置关系的 判断法;知道 标准二次曲 面;了解投影 柱面和投影 曲线。 12 课堂面授 教材对应 习题 培养学生具有 扎实的基础理 论知识,具备 学习和应用知 识能力、适应 能力、批判性 思维与创新能 力、终身学习 和自主学习能 力 课程目标 1,2

注1上:建议按照教学周周学时编排,以便自动生成教学日历。 注2:相应章节的课程思政融入点根据实际清况填写。 考核方式 ()平时作业10分 (2)期中考试30分 (Grading) (3)期末考试60分 ·教材成参考资 抖Textbooks 《大学数学一微积分》第二版(上册),2016年,上海交通大学数学系微积分课程组编 &Other 高等教育出版社,1SN978-7-04-045987-6 Materials) 其它(More) 备注(Noles) 备注说明: 带内容为必填项 2.课程简介字数为300-500字:课程大纲以表述清楚教学安排为宜,字数不限
注 1:建议按照教学周周学时编排,以便自动生成教学日历。 注 2:相应章节的课程思政融入点根据实际情况填写。 *考核方式 (Grading) (1)平时作业 10 分 (2)期中考试 30 分 (3)期末考试 60 分 *教材或参考资 料 (Textbooks & Other Materials) 《大学数学--微积分》第二版(上册),2016 年,上海交通大学数学系微积分课程组编, 高等教育出版社,ISBN 978-7-04-045987-6 其它(More) 备注(Notes) 备注说明: 1.带*内容为必填项。 2.课程简介字数为 300-500 字;课程大纲以表述清楚教学安排为宜,字数不限