
《偏微分方程》课程教学大纲 课程基本信息(Course Information) 津程代码 学时 学分 (Course Code MATH 3503 Credit Hour +课程名称 (中文)偏微分方程 (Course Name 英文)Partial Differential Equations 果程类型(Cou 专业核心选修课/Coreelective course Type) 授课对象(Tg 数学与应用数学专业本科生/ Audience) undergraduate students majoringin Mathematics and Applied Mathematics 授课语言 全中文/Chinese Instruction) 开课院系 数学科学学院/School of Mathematical Sciences (School) 先修课程 微积分,线性代数,常微分方程/Calculus 后续课程 偏微分方程续论 (Prerequisite) Linear Algebra,Ordinary Differential Equations (post) 课程网 址 *课程负责人 李亚纯Yachun Li (Instructor) Webpag “偏微分方程”是数学学科中分析类课程的重要基础课程,它在数学的其 课程简介(中文 支和自然科学与工程技术中的广泛应用是众所周知的。本课程将尽可能 (Description) 结合物理背景,系统地对几类典型偏微分方程数学结构、求解方法、解的性 质以及物理意义进行详细闸述,为学生日后的学习和工作打下坚实的基础, 提供强有力的工具。 his course is an important basic course among the analysis courses in mathematics.It as wide applications in other branches of mathematics and natural sciencesas well as 课积简介(英文 engineering technology.In this course,combining with physical background as much as (Description) severaltypical typesof oout mathematical stru ures sol ing metho
《偏微分方程》课程教学大纲 课程基本信息(Course Information) 课程代码 (Course Code) MATH 3503 *学时 (Credit Hours) 48 *学分 (Credits) 3 *课程名称 (Course Name) (中文)偏微分方程 (英文)Partial Differential Equations 课程类型 (Course Type) 专业核心选修课/Coreelective course 授课对象(Target Audience) 数学与应用数学专业本科生/ undergraduate students majoring in Mathematics and Applied Mathematics 授课语言 (Language of Instruction) 全中文/Chinese *开课院系 (School) 数学科学学院/School of Mathematical Sciences 先修课程 (Prerequisite) 微积分,线性代数,常微分方程/Calculus, Linear Algebra, Ordinary Differential Equations 后续课程 (post) 偏微分方程续论 *课程负责人 (Instructor) 李亚纯/Yachun Li 课程网 址 (Course Webpage ) *课程简介(中文) (Description) “偏微分方程”是数学学科中分析类课程的重要基础课程,它在数学的其它 分支和自然科学与工程技术中的广泛应用是众所周知的。本课程将尽可能地 结合物理背景,系统地对几类典型偏微分方程数学结构、求解方法、解的性 质以及物理意义进行详细阐述,为学生日后的学习和工作打下坚实的基础, 提供强有力的工具。 *课程简介(英文) (Description) This course is an important basic course among the analysis courses in mathematics. It has wide applications in other branches of mathematics and natural sciencesas well as engineering technology. In this course,combining with physical background as much as possible, we introducesystematically several typical types of partial differential equations about mathematical structures,solving methods, properties of solutions, and physical meaningsin details
课程目标与内容(Course objectives and contents) 在为学生日后的学习和工作打下坚实的基础,提供强有力的工具,更好地服务于国 家建设.(A,C1,D1) 理程目标 学生能掌握偏微分方程的基本原理和基本方法,初步了解偏微分方程的理论体系。 (Course Objeet) 思维方式和研究方法。 (B1,B2 为学生进一步了解和应用现代偏微分方程的有关内容提供重要帮助提高学生的丝 合学习能力.(B4,C3,C5) 培养学生用分析的方法建模和解决实际问题的能力(B3,D2) 章节 教学内容(要点) 学时 敦学作业及考课程思政对应课 形式 核腰求 融入点 程日 3引论: 第、偏微分方程简介 课 每 典型方程的数学横型 10 果堂教学 2 二阶线性偏微分方程简介 后有课 作业,要求 波动方程: 通过课理 电立完成 弦振动方程Cauchv问题 课堂 学习和平 有时 弦振动方程初边值问题 时作业心 *敦学内容进度 2 高雄波动方程 教学 排及对应课程 及思考题 解的唯一性与稳定性 生思考 培养学生 标(Clas 学生要经 价双曲型方程组: 一丝不苟 Schedule 过认真思 课堂 认直严谨 Requirements 一阶线性偏微分方程组简介 8 考、相互 两个白变量的一阶线性双曲型方 Course obiective 教学 的工作作 等方 风,培养 热传导方程: 式才能解 生刻苦务 初边值问题 课堂 实、意志坚 6 初值问题 教学 牌的生活 解的唯一性与稳定性 3.安排 态度, 调和方程: 作业中的 调和函数的基本性质 12 课堂 可题集中 2。 Green函数 3.调和函数的进一步性质 进行讲解 考核方式 ()平时成绩50分(上课参与程度、作业、综合性思考题、小测验、大作业等) (Grading) (2)期末考试50分 教材或参考资米 牧材:《数学物理方程》(第三版),谷超豪、李大潜、陈恕行、郑宋穆、谭永基,高 (Textbooks 等教育出板社,2012年 Other Materials 其它(Morc) 备注(Notes)
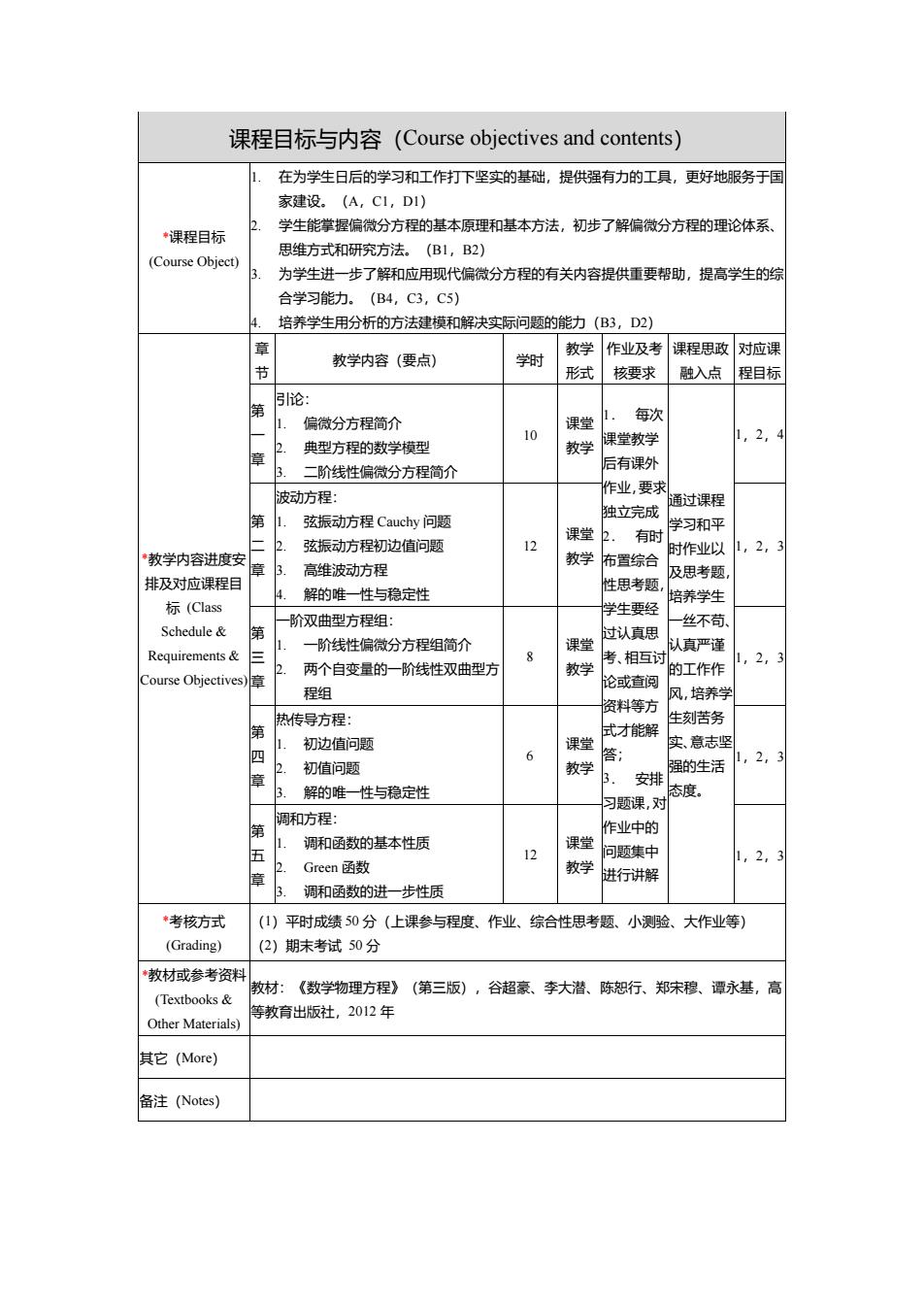
课程目标与内容(Course objectives and contents) *课程目标 (Course Object) 1. 在为学生日后的学习和工作打下坚实的基础,提供强有力的工具,更好地服务于国 家建设。(A,C1,D1) 2. 学生能掌握偏微分方程的基本原理和基本方法,初步了解偏微分方程的理论体系、 思维方式和研究方法。(B1,B2) 3. 为学生进一步了解和应用现代偏微分方程的有关内容提供重要帮助,提高学生的综 合学习能力。(B4,C3,C5) 4. 培养学生用分析的方法建模和解决实际问题的能力(B3,D2) *教学内容进度安 排及对应课程目 标 (Class Schedule & Requirements & Course Objectives) 章 节 教学内容(要点) 学时 教学 形式 作业及考 核要求 课程思政 融入点 对应课 程目标 第 一 章 引论: 1. 偏微分方程简介 2. 典型方程的数学模型 3. 二阶线性偏微分方程简介 10 课堂 教学 1. 每次 课堂教学 后有课外 作业,要求 独立完成 2. 有时 布置综合 性思考题, 学生要经 过认真思 考、相互讨 论或查阅 资料等方 式才能解 答; 3. 安排 习题课,对 作业中的 问题集中 进行讲解 通过课程 学习和平 时作业以 及思考题, 培养学生 一丝不苟、 认真严谨 的工作作 风,培养学 生刻苦务 实、意志坚 强的生活 态度。 1,2,4 第 二 章 波动方程: 1. 弦振动方程 Cauchy 问题 2. 弦振动方程初边值问题 3. 高维波动方程 4. 解的唯一性与稳定性 12 课堂 教学 1,2,3 第 三 章 一阶双曲型方程组: 1. 一阶线性偏微分方程组简介 2. 两个自变量的一阶线性双曲型方 程组 8 课堂 教学 1,2,3 第 四 章 热传导方程: 1. 初边值问题 2. 初值问题 3. 解的唯一性与稳定性 6 课堂 教学 1,2,3 第 五 章 调和方程: 1. 调和函数的基本性质 2. Green 函数 3. 调和函数的进一步性质 12 课堂 教学 1,2,3 *考核方式 (Grading) (1)平时成绩 50 分(上课参与程度、作业、综合性思考题、小测验、大作业等) (2)期末考试 50 分 *教材或参考资料 (Textbooks & Other Materials) 教材:《数学物理方程》(第三版),谷超豪、李大潜、陈恕行、郑宋穆、谭永基,高 等教育出版社,2012 年 其它(More) 备注(Notes)