《实变函数》课程教学大纲 课程基本信息(Course Information) 学时 课程代码 (Cr 学分 MATH 3605 3 (Course Code dit Hours (Credits) ·课程名称 (中文)实变函数 (Course Name) 英文)Real Analysis 课程类型 专业必修课 (Course Type) 授课对象 (Target 本科生 Audicnce) 授课语言 (Language of 双语(中文授课,英文教材) Instruction) 开课院系 数学科学学院 (School) 先修课程 后续 《数学分析》 课程《泛函分析》,《随机分析》等 (Prerequisite) (post) 网址 课程负责人 徐永忠 (Cou (Instructor) e Webpa ge) 《实变函数》是一门数学系重要的专业基础课程,这是一门以证明为主的 课程。它的主要任务是通过各教学环节,使学生掌握Lebesgue测度,Lebesgue 课程简个(中积分及收敛性定理,Fub定理,有界变差函数和绝对连续函数的基本性质。 ) (Description) 和抽象测度理论和Radon-Nikodvn导数。本课程不仅对数学专业的学生很重要 对学习应用数学,机器学习的理论基础,概率统计和金融等专业也很重要,为 学生进一步学习泛函分析,偏微分方程,机器学习理论,概率统计和随机过程 等方向打下坚实的基础
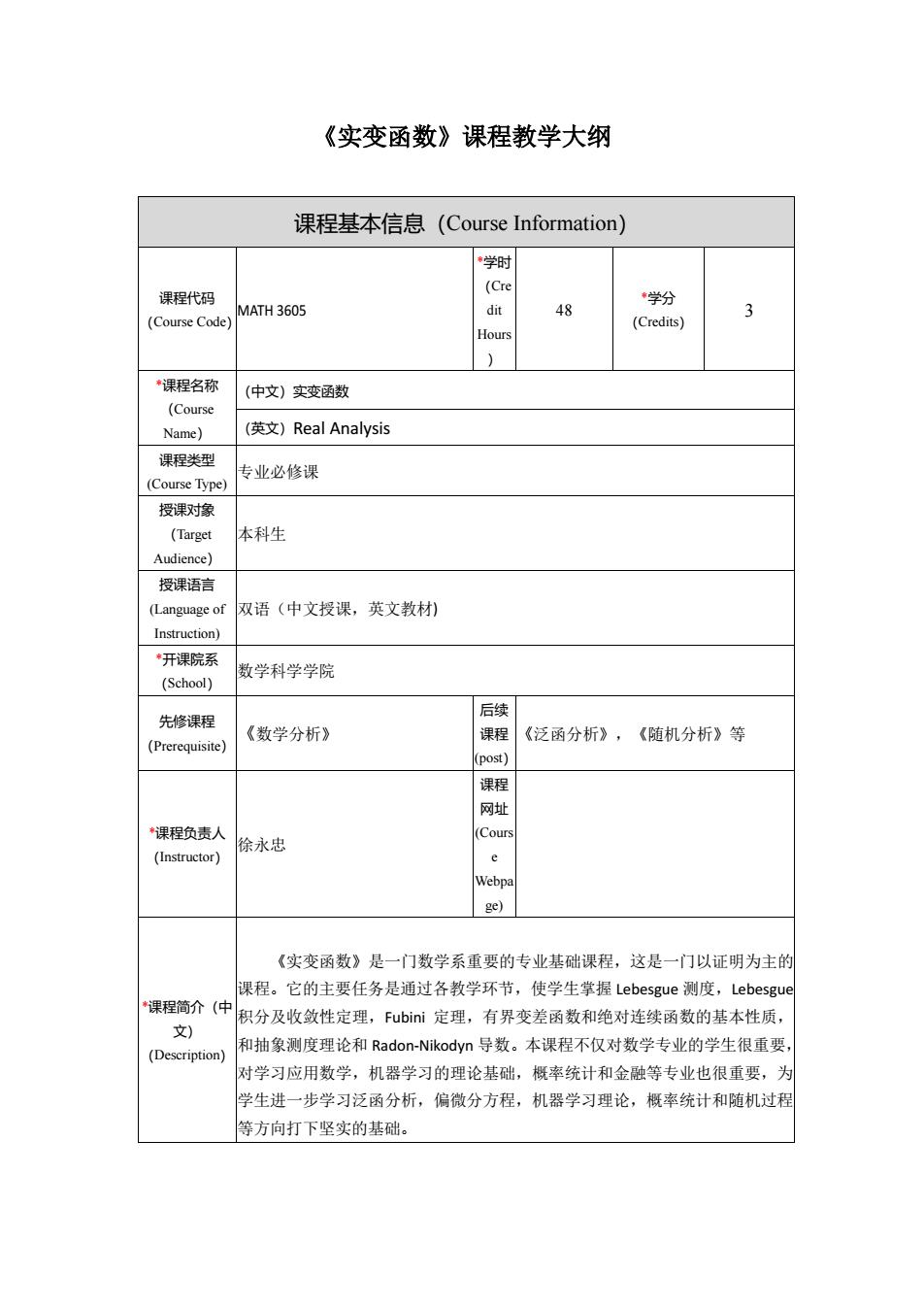
《实变函数》课程教学大纲 课程基本信息(Course Information) 课程代码 (Course Code) MATH 3605 *学时 (Cre dit Hours ) 48 *学分 (Credits) 3 *课程名称 (Course Name) (中文)实变函数 (英文)Real Analysis 课程类型 (Course Type) 专业必修课 授课对象 (Target Audience) 本科生 授课语言 (Language of Instruction) 双语(中文授课,英文教材) *开课院系 (School) 数学科学学院 先修课程 (Prerequisite) 《数学分析》 后续 课程 (post) 《泛函分析》,《随机分析》等 *课程负责人 (Instructor) 徐永忠 课程 网址 (Cours e Webpa ge) *课程简介(中 文) (Description) 《实变函数》是一门数学系重要的专业基础课程,这是一门以证明为主的 课程。它的主要任务是通过各教学环节,使学生掌握 Lebesgue 测度,Lebesgue 积分及收敛性定理,Fubini 定理,有界变差函数和绝对连续函数的基本性质, 和抽象测度理论和 Radon-Nikodyn 导数。本课程不仅对数学专业的学生很重要, 对学习应用数学,机器学习的理论基础,概率统计和金融等专业也很重要,为 学生进一步学习泛函分析,偏微分方程,机器学习理论,概率统计和随机过程 等方向打下坚实的基础

The Course is one of the core courses for the above majors.The following topic ered in thisou measure and measurable functions:exterior measure,Lebesgu measure and properties of measurable sets,measurable functions and thei properties,Egorov theorem. 2)Lebesgue integral,convergence theorems and Fubini theorem:How to define Lebesgue integral starting from simple functions,Riemann integral and Lebesgue integr ab 课程简介(英Lebesgue integrable functions,the proof and applications of Fubini theorem 文) the space of Lebesgue integral functions and its properties. (Description)3)Differentiability of functions of bounded variations,absolutely continuous functions:definitions and properties. 4)Abstract measure spaces and Radon-Nikodyn derivatives:definitions and several important examples. This course is an important prerequisite not only for math major,but also field such as theoretical foundation of machine learning,financial engineering, tochastic. 课程目标与内容(Course objectives and contents) 通过这门课程的学习,学生要掌握如下的知识点,掌握测度空间及其上的积分 理论。这是数学,概率统计,经济学,金融学和数据科学的重要理论基础和描 述工具。 通过这门课程的学习,学生要学会如何做严格的证明推理,学习认真求实,慎 密推理的思维习惯和工作态度。 ()Lebesgue测度和可测函数:外测度,Lebesgue测度的定义及Lebesgue可测 集的基本性质,可测函数的定义和基本性质,Egorov定理,可测函数与连续函 “课程目标 数的关系。(A3,A4,B1,B2,C1,C3) (Course Object)(2)Lebesgue积分及收敛性定理,Fubini定理:如何从简单函数出发定义Lebesgue 积分,Lebesgue积分与Riemann积分的关系,几个重要的积分收敛性定理 Lebesgue可积函数的绝对连续性,Fubini定理的证明与应用.(A3,A4,B1,B2,C1,C3) 3)有界变差函数的定义及主要性质,绝对连续函数的定义及性质。 A3,A4,B1,B2,C1,C3) (4)抽象测度空间的定义,及其上的可测函数,积分的定义,Radon--Nikodyn号 数:定义和几个重要的例子。(A3,A4,B1,B2,B3,C1,C3,C5)
*课程简介(英 文) (Description) The Course is one of the core courses for the above majors. The following topics are covered in this course: 1) Lebesgue measure and measurable functions: exterior measure, Lebesgue measure and properties of measurable sets, measurable functions and their properties, Egorov theorem . 2) Lebesgue integral, convergence theorems and Fubini theorem: How to define Lebesgue integral starting from simple functions, Riemann integral and Lebesgue integral, important convergence theorems, absolute continuity of Lebesgue integrable functions, the proof and applications of Fubini theorem, the space of Lebesgue integral functions and its properties. 3) Differentiability of functions of bounded variations, absolutely continuous functions: definitions and properties. 4) Abstract measure spaces and Radon-Nikodyn derivatives: definitions and several important examples. This course is an important prerequisite not only for math major, but also fields such as theoretical foundation of machine learning, financial engineering, stochastic control etc. 课程目标与内容(Course objectives and contents) *课程目标 (Course Object) 通过这门课程的学习,学生要掌握如下的知识点,掌握测度空间及其上的积分 理论。这是数学,概率统计,经济学,金融学和数据科学的重要理论基础和描 述工具。 通过这门课程的学习,学生要学会如何做严格的证明推理,学习认真求实,慎 密推理的思维习惯和工作态度。 (1) Lebesgue 测度和可测函数:外测度,Lebesgue 测度的定义及 Lebesgue 可测 集的基本性质,可测函数的定义和基本性质,Egorov 定理,可测函数与连续函 数的关系。(A3,A4,B1,B2,C1,C3) (2) Lebesgue 积分及收敛性定理,Fubini 定理:如何从简单函数出发定义 Lebesgue 积分,Lebesgue 积分与 Riemann 积分的关系,几个重要的积分收敛性定理, Lebesgue 可积函数的绝对连续性,Fubini 定理的证明与应用。(A3,A4,B1,B2,C1,C3) (3) 有 界 变 差 函 数 的 定 义 及 主 要 性 质 , 绝 对 连 续 函 数 的 定 义 及 性 质 。 (A3,A4,B1,B2,C1,C3) (4) 抽象测度空间的定义,及其上的可测函数,积分的定义,Radon-Nikodyn 导 数:定义和几个重要的例子。(A3,A4,B1,B2,B3,C1,C3,C5)
作业及 章节 教学内容(要 教学目标 学时 教学 课程思政融入 形式 考核要 对应课程目标 点) 求 集合运算 让同学们养 热练掌握有 课堂习题 成认真求实 可数集合 第一节 关基本概念 基本点集邦 教学小测验 慎密严谨的A3,A4,B1,82, 定理 扑 思维习惯和C1,C3 工作态度 让同学们 Lebesgue 熟练掌有 成认真求实 第一章 度和可测函 数 关基本概念, 12同上同上 24节 慎密严谨的A3,A4,B1,82 思维习惯和 1.C3,C5 定理 工作态度 ebesgue积 让同学们养 熟练掌握有 成认真求实 第一章 份及收敛性 关基本概12同上同上 植素避谨 A3,A4,B1,B2 12节 定理 念,定理 @维习横和C1,G 教学内容讲度 工作态度 安排及对应课 让同学们养 程目标C 成认直求实, 第一高 Schedule& Fubini定理同上 4同上同上 A3.A4.B1.B2 慎密严谨的 第三书 C1C3 Requirements 思维习惯 Course 工作态度 Objectives) 让同学们养 成认真求实,A3,A4,B1,B2 第三章局部可积函 第一节数均值定理 2同上同上 慎密严谨的C1.C3 思维习惯和 作态度 让回学们养 成认直求实, 第三音 有界变差函 A3.A4.B1.B2 第三节 同上同上 工作态度 让同学们养 成认直求空」 第三章绝对连续 2 同上同上 慎密严谨的A3,A4,B1,B2 第三节 思维习惯和C1,C3 工作态度 让同学们养A3,A4,B1,B2 3节向,其上的 2 同上同上 成认真求实,C1,C3
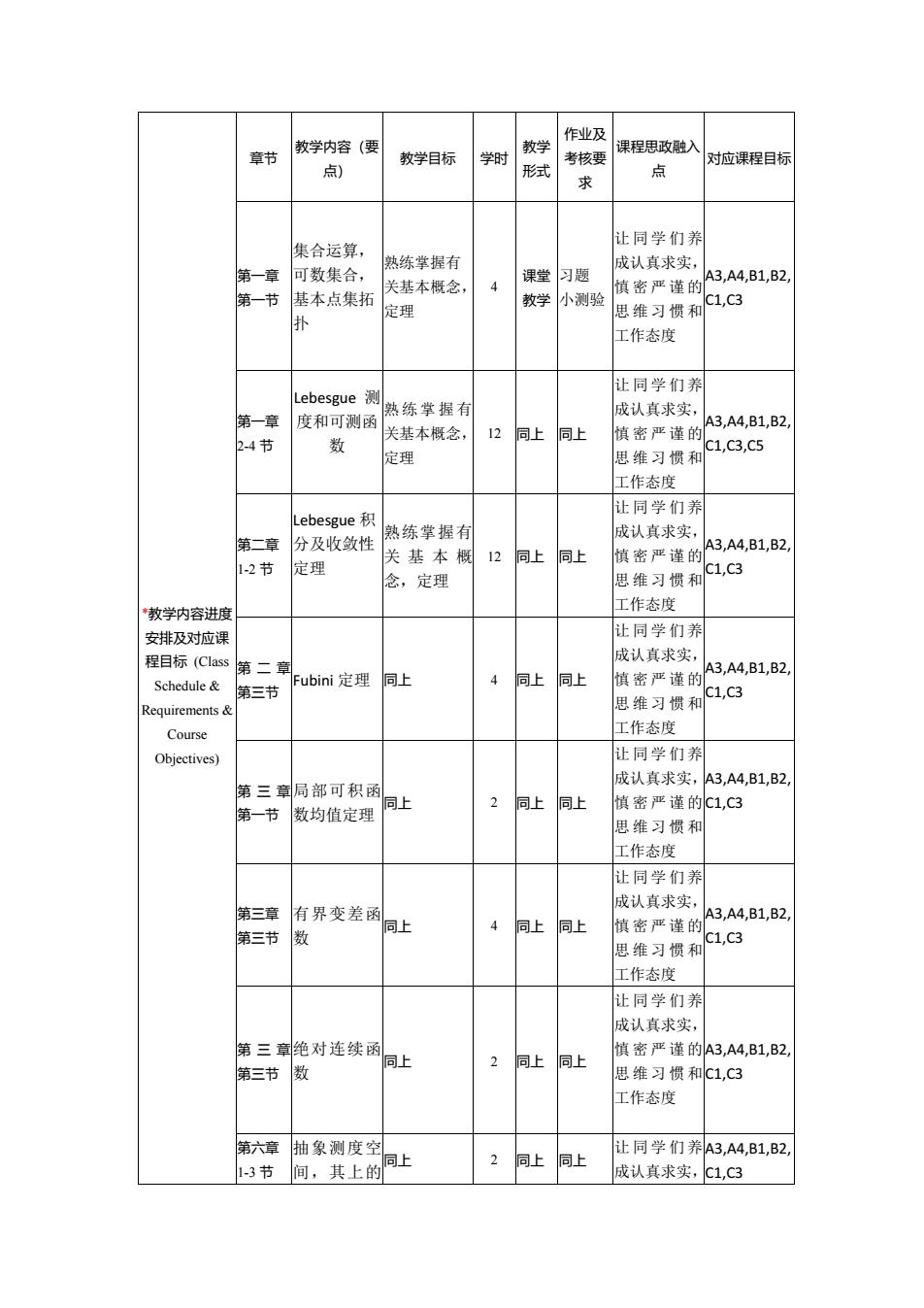
*教学内容进度 安排及对应课 程目标 (Class Schedule & Requirements & Course Objectives) 章节 教学内容(要 点) 教学目标 学时 教学 形式 作业及 考核要 求 课程思政融入 点 对应课程目标 第一章 第一节 集合运算, 可数集合, 基本点集拓 扑 熟练掌握有 关基本概念, 定理 4 课堂 教学 习题 小测验 让同学们养 成认真求实, 慎密严谨的 思维习惯和 工作态度 A3,A4,B1,B2, C1,C3 第一章 2-4 节 Lebesgue 测 度和可测函 数 熟练掌握有 关基本概念, 定理 12 同上 同上 让同学们养 成认真求实, 慎密严谨的 思维习惯和 工作态度 A3,A4,B1,B2, C1,C3,C5 第二章 1-2 节 Lebesgue 积 分及收敛性 定理 熟练掌握有 关 基 本 概 念,定理 12 同上 同上 让同学们养 成认真求实, 慎密严谨的 思维习惯和 工作态度 A3,A4,B1,B2, C1,C3 第二章 第三节 Fubini 定理 同上 4 同上 同上 让同学们养 成认真求实, 慎密严谨的 思维习惯和 工作态度 A3,A4,B1,B2, C1,C3 第三章 第一节 局部可积函 数均值定理 同上 2 同上 同上 让同学们养 成认真求实, 慎密严谨的 思维习惯和 工作态度 A3,A4,B1,B2, C1,C3 第三章 第三节 有界变差函 数 同上 4 同上 同上 让同学们养 成认真求实, 慎密严谨的 思维习惯和 工作态度 A3,A4,B1,B2, C1,C3 第三章 第三节 绝对连续函 数 同上 2 同上 同上 让同学们养 成认真求实, 慎密严谨的 思维习惯和 工作态度 A3,A4,B1,B2, C1,C3 第六章 1-3 节 抽象测度空 间,其上的同上 2 同上 同上 让同学们养 成认真求实, A3,A4,B1,B2, C1,C3

积分和收敛 慎密严谨的 性定理, 思维习惯利 型例子 工作态度 让同学们养 成认真求实, 第六Radon-Nikad 2同上同上 A3.A4.B1.B2 同 植案避谨的 第四节N导数 维习横和C1,,G5 工作态度 让同学们养 D空间 成认真求实, 卧充 Holder不 a 同上同上 慎密严谨的A3,A4,B1,B2 思维习惯和C1,C,c5 工作态度 课堂 让同学们养 成认直求宽 复习 2 程目标 小组 慎密严谨 讨 思维习惯 R-a 工作态度 注1:津议按照款学周周学时 以便自动生成教学日历。 注2:相应章节的课程思政融入 根 (1)平时作业20分 考核方式 (2)小测验15分 (Grading) (3)期末小论文15分 (4)期未考试50分 l.主要教材:EliasStein和Rami Shakarchi著,Real Analysis,,世界图书出 教材或参考洛 版公司.2010版,ISBN:9787506282383 料(Textbooks &Other ials) 2.辅助教材:实变函数与泛函分析,郭懋正著,北京大学出版社,2005版, 5BN:9787301078570 其它(More) 备注Notes)
积分和收敛 性定理,典 型例子 慎密严谨的 思维习惯和 工作态度 第六章 第四节 Radon-Nikod y 导数 同上 2 同上 同上 让同学们养 成认真求实, 慎密严谨的 思维习惯和 工作态度 A3,A4,B1,B2, C1,C3,C5 补充内 容 L^p 空间, Holder 不等 式 同上 2 同上 同上 让同学们养 成认真求实, 慎密严谨的 思维习惯和 工作态度 A3,A4,B1,B2, C1,C3,C5 复习 2 课堂 答疑 小组 讨论 让同学们养 成认真求实, 慎密严谨的 思维习惯和 工作态度 课 程 目 标 1-4 注 1:建议按照教学周周学时编排,以便自动生成教学日历。 注 2:相应章节的课程思政融入点根据实际情况填写。 *考核方式 (Grading) (1)平时作业 20 分 (2)小测验 15 分 (3)期末小论文 15 分 (4)期末考试 50 分 *教材或参考资 料 (Textbooks & Other Materials) 1.主要教材: EliasStein 和 Rami Shakarchi 著,Real Analysis,世界图书出 版公司,2010 版,ISBN:9787506282383 2.辅助教材:实变函数与泛函分析,郭懋正著,北京⼤学出版社,2005 版, ISBN:9787301078570 其它(More) 备注(Notes)