
《泛函分析》课程教学大纲 课程基本信息(Course Information) 课程代码 *学时 (Cours MATH3611 Code) Hours) *课程名称 (仲文】泛函分析 (Course Name) (英文)Functional Analysis 课程类型 专业核心选修 (Course Type) 授课对象 (Target B年级本科生 Audience) 授课语言 (Language of双语 Instruction) “开课院系 数学科学学院 (School) 先修课程 数学分析、线性代数、 后续课程 (Prerequisite 实变函数 (post) ·课程负责人 课程网址 谢春景 (Course ttps://oc situ.edu.cn/courses/31126 (Instructor) (仲文30-500字,含课程性质 主要教学内容、课程救学目标等)】 本课程为数学专业的本科生高年级选修课,是泛函分析的入门课程。主要教学内容包括度量空间,线性空间 *课程简介(中及线性映射,Hahn-Banach定理及其应用,赋范线性空间,Hilbert空间及其应用,威范线性空间的对偶,弱 文) 收敛与弱·收敛,有界线性算子,谱理论简介,紧算子理论等。课程的教学目标是使学生能够了解泛函分析 (Description)的基本思想及其在偏微分方程及其他现代数学分支中的广泛的应用,如压缩陕射原理,无穷维线性空间的是 本性质,R表示定理,一致有界定理,开映射定理,闭图像定理等.同时为学生进一步深入学习泛函 析的相关内容如自伴算子、半群理论以及快速进入数学研究的前沿领域等奠定坚实的基础。 (英文300-500字) This is an introductory course for functional analysis and it is a selective course for senor students.The maior topi 课程简介(英 nclude spacesand maps Hahn-Banach Theoremand Nomed linear paces,Hilbert spac ces and its application convergence,bounded linear operators,elementary spectral theory,compact maps,et.The objective of the course (Description tolet the students understand the basic ideas of functioalysis and its brod applications in partial different equations and other branches of modern mathematics.such as contraction map theorem.basic properties of infinite
《泛函分析》课程教学大纲 课程基本信息(Course Information) 课程代码 (Course Code) MATH3611 *学时 (Credit Hours) 48 *学分 (Credits) 3 *课程名称 (Course Name) (中文)泛函分析 (英文)Functional Analysis 课程类型 (Course Type) 专业核心选修 授课对象 (Target Audience) 3 年级本科生 授课语言 (Language of Instruction) 双语 *开课院系 (School) 数学科学学院 先修课程 (Prerequisite ) 数学分析、线性代数、 实变函数 后续课程 (post) *课程负责人 (Instructor) 谢春景 课程网址 (Course Webpage) https://oc.sjtu.edu.cn/courses/31126 *课程简介(中 文) (Description) (中文 300-500 字,含课程性质、主要教学内容、课程教学目标等) 本课程为数学专业的本科生高年级选修课,是泛函分析的入门课程。主要教学内容包括度量空间,线性空间 及线性映射,Hahn-Banach 定理及其应用,赋范线性空间,Hilbert 空间及其应用,赋范线性空间的对偶,弱 收敛与弱*收敛,有界线性算子,谱理论简介,紧算子理论等。课程的教学目标是使学生能够了解泛函分析 的基本思想及其在偏微分方程及其他现代数学分支中的广泛的应用,如压缩映射原理,无穷维线性空间的基 本性质,Riesz 表示定理,一致有界定理,开映射定理,闭图像定理等。同时为学生进一步深入学习泛函分 析的相关内容如自伴算子、半群理论以及快速进入数学研究的前沿领域等奠定坚实的基础。 *课程简介(英 文) (Description) (英文 300-500 字) This is an introductory course for functional analysis and it is a selective course for senior students. The major topics include metric spaces, linear spaces and linear maps, Hahn-Banach Theorem and its applications, Normed linear spaces, Hilbert spaces and its applications, dual for normed linear spaces, weak convergence and weak* convergence, bounded linear operators, elementary spectral theory, compact maps, etc. The objective of the course is to let the students understand the basic ideas of functional analysis and its broad applications in partial differential equations and other branches of modern mathematics, such as contraction map theorem, basic properties of infinite dimensional linear spaces, Riesz representation theorem, principle of uniform boundedness, open mapping theorem
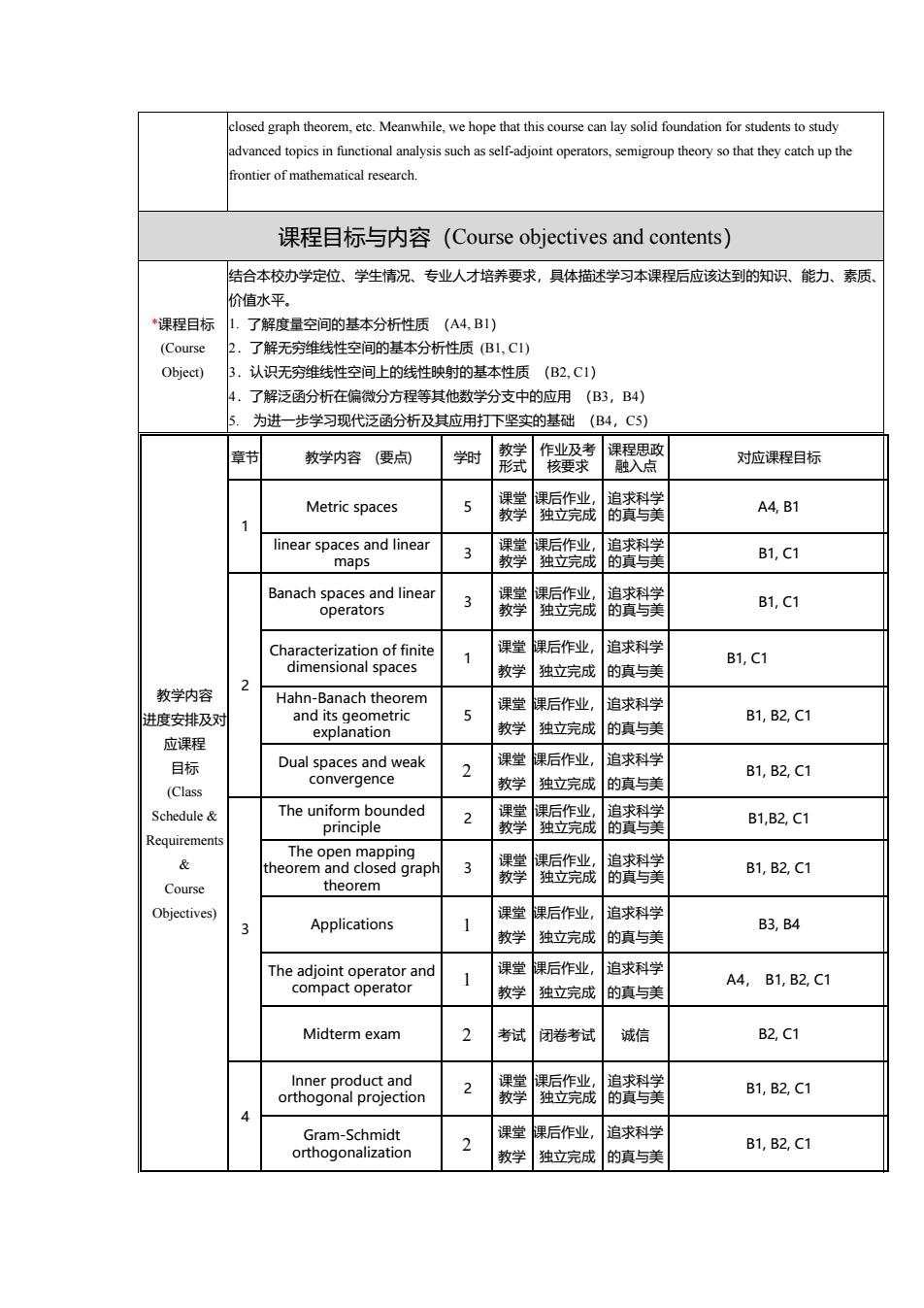
closed graph theorem.etc.Meanwhile.we hope that this course can lay solid foundation for students to studv advanced topics in functional nalysis sefadjoint operators,semigroup frontier of mathematical research 课程目标与内容(Course objectives and contents)) 结合本校办学定位、学生情况、专业人才培养要求,具体描述学习本课程后应该达到的知识、能力、素质、 价值水平. “课程目标1.了解度量空间的基本分析性质(A4,B1) (Course 上.了解无穷维线性空间的基本分析性质(B1,C1) Object) 3认识无维线性空间上的线性钟时的其本性质B2C1} 了解泛函 分方程等其 数学分支 中的应用 (B3,B4 为进一步学习现代泛函分析及其应用打下坚实的基础(4,C5】 章节 教学内容(要点 学时 对应课程目标 Metric spaces 5 A4,B1 earpndhaT7 3 B1,C1 Banach spa and linear operator 3 B1,C1 课堂课后作业, 追求科学 1 的真与美 B1,C1 教学内容 2 教学独立完成 Hahn-Banach theorem 5 课堂课后作业 追求科学 进度安排及风 B1,B2,C1 教学 独立完成 的真与美 应课程 explanation 目标 2 课堂课后作业 追求科学 B1,B2,C1 (Class 教学独立完成 的直与美 Schedule The untoouned 2 B1,B2,C1 Requirement 3 高 B1,B2,C1 Course theorem Obiectives 课堂课后作业 追求科学 Applications 1 教学独立完成 的真与美 B3,B4 Compact The adjoint opera 堂课后作业, 追求科学 1 学 独立完成 的真与美 A4,B1,B2,C1 Midterm exam 考试 闭卷考记 诚信 B2,C1 2 B1.B2.C1 Gram-Schmidt 2 课堂 课后作业 追求科学 orthogonalization 教学独立完成的真与美 B1.B2.C1
closed graph theorem, etc. Meanwhile, we hope that this course can lay solid foundation for students to study advanced topics in functional analysis such as self-adjoint operators, semigroup theory so that they catch up the frontier of mathematical research. 课程目标与内容(Course objectives and contents) *课程目标 (Course Object) 结合本校办学定位、学生情况、专业人才培养要求,具体描述学习本课程后应该达到的知识、能力、素质、 价值水平。 1. 了解度量空间的基本分析性质 (A4, B1) 2.了解无穷维线性空间的基本分析性质 (B1, C1) 3.认识无穷维线性空间上的线性映射的基本性质 (B2, C1) 4.了解泛函分析在偏微分方程等其他数学分支中的应用 (B3,B4) 5. 为进一步学习现代泛函分析及其应用打下坚实的基础 (B4,C5) 教学内容 进度安排及对 应课程 目标 (Class Schedule & Requirements & Course Objectives) 章节 教学内容 (要点) 学时 教学 形式 作业及考 核要求 课程思政 融入点 对应课程目标 1 Metric spaces 5 课堂 教学 课后作业, 独立完成 追求科学 的真与美 A4, B1 linear spaces and linear maps 3 课堂 教学 课后作业, 独立完成 追求科学 的真与美 B1, C1 2 Banach spaces and linear operators 3 课堂 教学 课后作业, 独立完成 追求科学 的真与美 B1, C1 Characterization of finite dimensional spaces 1 课堂 教学 课后作业, 独立完成 追求科学 的真与美 B1, C1 Hahn-Banach theorem and its geometric explanation 5 课堂 教学 课后作业, 独立完成 追求科学 的真与美 B1, B2, C1 Dual spaces and weak convergence 2 课堂 教学 课后作业, 独立完成 追求科学 的真与美 B1, B2, C1 3 The uniform bounded principle 2 课堂 教学 课后作业, 独立完成 追求科学 的真与美 B1,B2, C1 The open mapping theorem and closed graph theorem 3 课堂 教学 课后作业, 独立完成 追求科学 的真与美 B1, B2, C1 Applications 1 课堂 教学 课后作业, 独立完成 追求科学 的真与美 B3, B4 The adjoint operator and compact operator 1 课堂 教学 课后作业, 独立完成 追求科学 的真与美 A4, B1, B2, C1 Midterm exam 2 考试 闭卷考试 诚信 B2, C1 4 Inner product and orthogonal projection 2 课堂 教学 课后作业, 独立完成 追求科学 的真与美 B1, B2, C1 Gram-Schmidt orthogonalization 2 课堂 教学 课后作业, 独立完成 追求科学 的真与美 B1, B2, C1
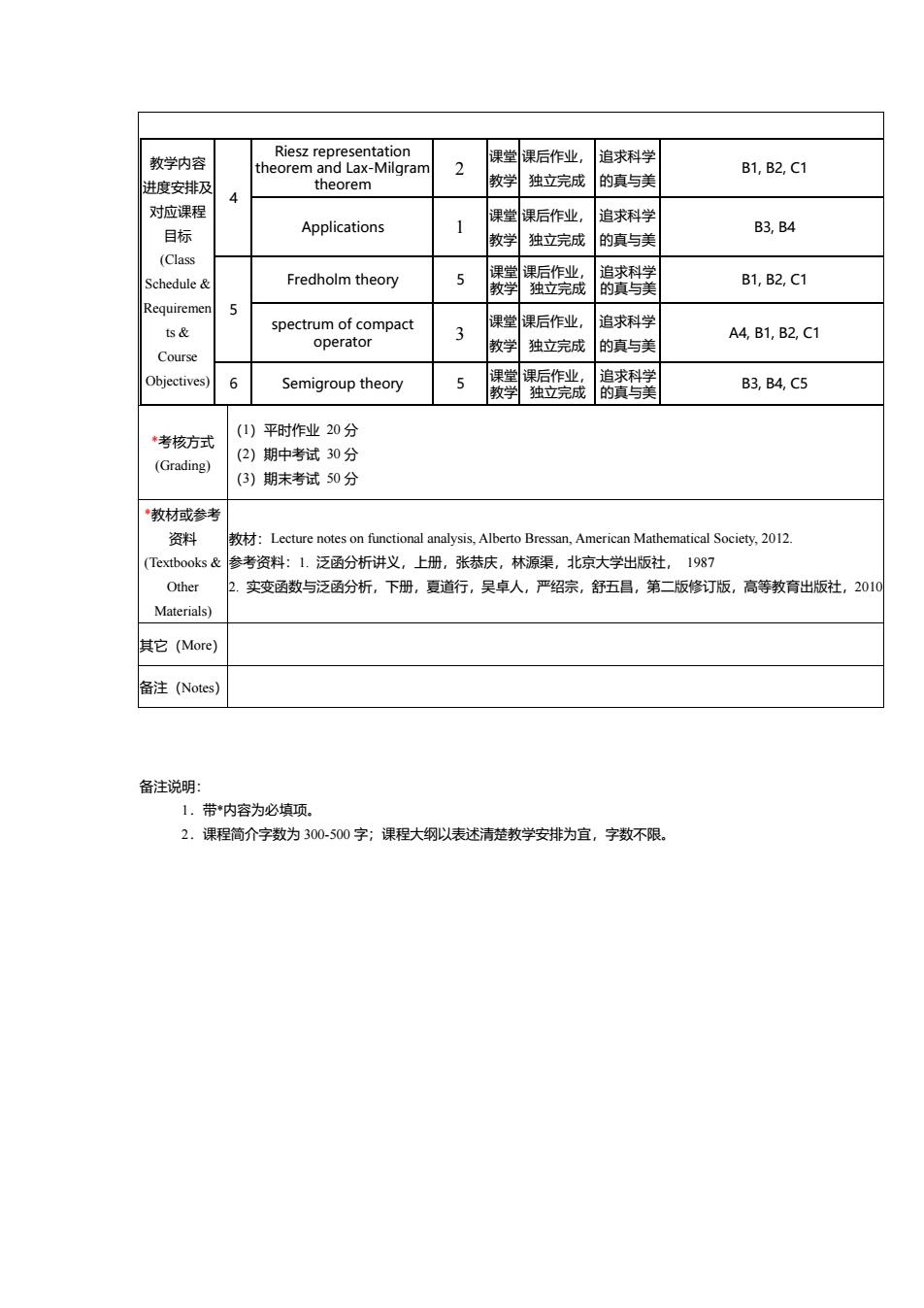
教学内容 课堂课后作业,追求科学 B1,B2,C1 进度安排) theorem 教学独立完成的真与美 对应课理 Applications 课学课后作业, 追求科学 目标 B3,B4 教学 独立完成 的真与美 Fredholm theory B1,B2,C1 Requireme ts& spectrum of compact 课堂课后作业, 追求科学 A4.B1.B2.C1 operator Course 教学独立完成 的真与美 6 Semigroup theory 5 科 B3,B4,C5 *考核方式 ()平时作业20分 (2)期中考试30分 (Grading) (3)期末考试50分 教材或参老 资料 American Mathematical Society,2012 (Textbooks&参考资料:1.泛函分析讲义,上册,张恭肤,林源渠,北京大学出版社,1987 Other 上.实变函数与泛函分析,下册,夏道行,吴卓人,严绍宗,舒五目,第二版修订版。高等教出版社,2010 Materials) 其它(More) 备注(Noes) 备注说明: 1.带内容为必填项。 2.课程简介字数为300-500字;课程大纲以表述清楚教学安排为宜,字数不限
教学内容 进度安排及 对应课程 目标 (Class Schedule & Requiremen ts & Course Objectives) 4 Riesz representation theorem and Lax-Milgram theorem 2 课堂 教学 课后作业, 独立完成 追求科学 的真与美 B1, B2, C1 Applications 1 课堂 教学 课后作业, 独立完成 追求科学 的真与美 B3, B4 5 Fredholm theory 5 课堂 教学 课后作业, 独立完成 追求科学 的真与美 B1, B2, C1 spectrum of compact operator 3 课堂 教学 课后作业, 独立完成 追求科学 的真与美 A4, B1, B2, C1 6 Semigroup theory 5 课堂 教学 课后作业, 独立完成 追求科学 的真与美 B3, B4, C5 *考核方式 (Grading) (1)平时作业 20 分 (2)期中考试 30 分 (3)期末考试 50 分 *教材或参考 资料 (Textbooks & Other Materials) 教材:Lecture notes on functional analysis, Alberto Bressan, American Mathematical Society, 2012. 参考资料:1. 泛函分析讲义,上册,张恭庆,林源渠,北京大学出版社, 1987 2. 实变函数与泛函分析,下册,夏道行,吴卓人,严绍宗,舒五昌,第二版修订版,高等教育出版社,2010 其它(More) 备注(Notes) 备注说明: 1.带*内容为必填项。 2.课程简介字数为 300-500 字;课程大纲以表述清楚教学安排为宜,字数不限