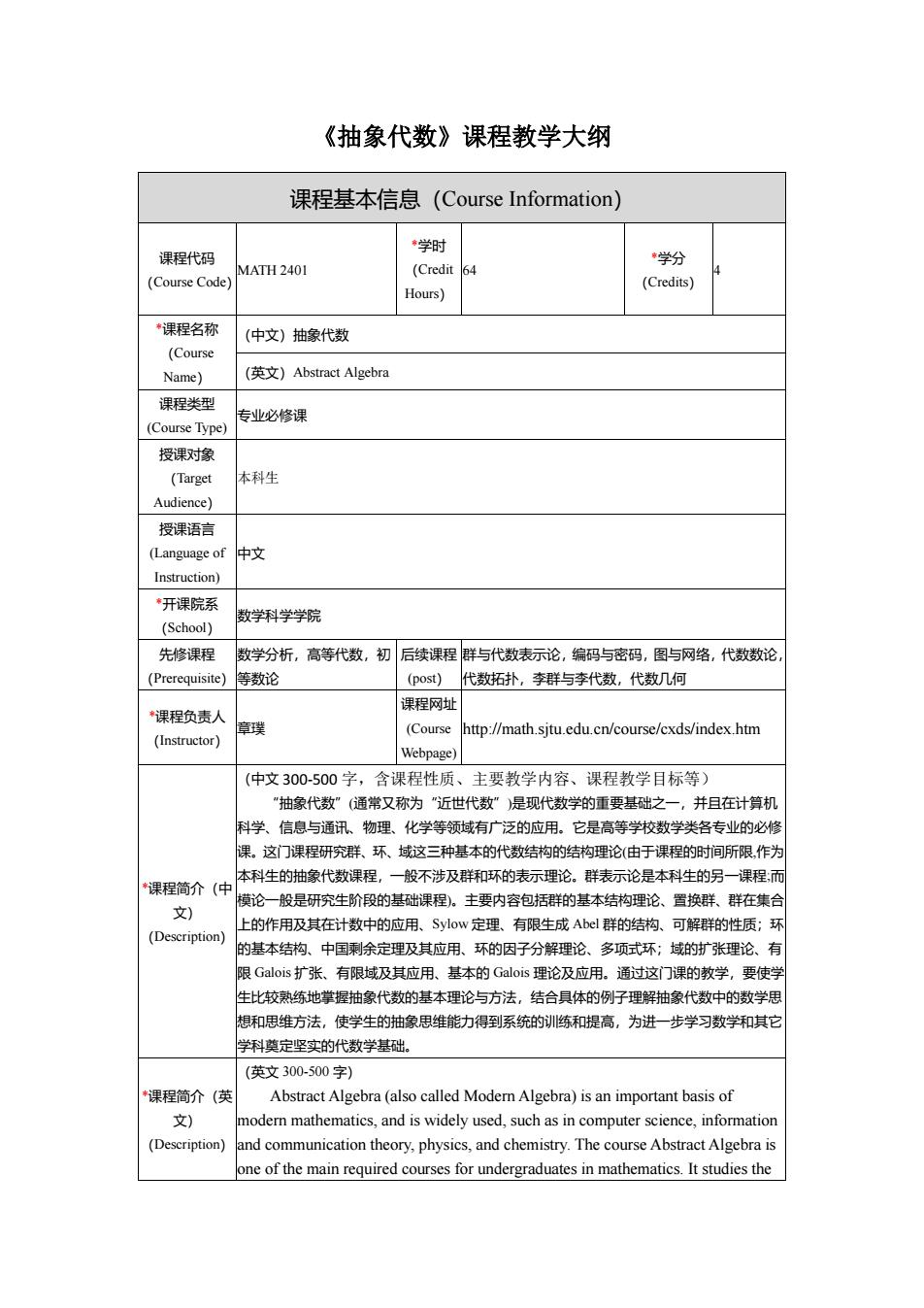
《抽象代数》课程教学大纲 课程基本信息(Course Information) 课程代码 *学时 MATH 240 (Credit 4 学粉 (Course Code Hours) (Credits) “课程名称 (中文)抽象代敌 (Course Name) (英文)Abstract Algebra 课程类型 (Course Typ 专业必修课 授课对象 (Target 本科生 Audience) 授课语言 (Language of 中文 Instruction) 开课院系 数学科学学院 先修课程 数学分析,高等代数,初后续课程群与代数表示论,编码与密码,图与网络,代数数论 (Prerequisite)等数论 (pos)代数拓扑,李群与李代数,代数几何 “课程负责人 课程网址 (Course http://math.sjtu.edu.cn/course/cxds/index.htm (Instructor) Webpage) (中文300-500字,含课程性质、主要教学内容、课程教学目标等) 抽象代数堂又弥为"诉世代数是现代数学的要础之一 科学、信息与通讯、物理、化学等 域 广泛的应用 它是高等学校数学类各专业的 课。这门课程研究群、环、域这三种基本的代数结构的结构理论(由于课程的时间所限作为 课程简介(中 本科生的抽象代数课程,一般不涉及群和环的表示理论。群表示论是本科生的另一课程而 模论一股是研究生阶段的基础课程。主要内容包括群的基本结构理论、置换群、群在集合 文) 上的作用及其在计数中的应用、Svow定理.有限生成Ab群的结构。可解群的性质:环 (Description) 的基本结构、中国剩余定理及其应用、环的因子分解理论、多项式环域的射张理论 限Gaos扩张、有限域及具应用、基本的Galois理论及应用。通过这门课的教学,要使 生比较熟练地掌握抽象代数的基本理论与方法,结合具体的例子理解抽象代数中的数学凭 想和思维方法,使学生的抽象思维能力得到系统的训练和提高,为进一步学习数学和其它 学利奠定坚实的代数学基础。 (英文300-500字 课程简介(英 Abstract Algebra(also called Modem Algebra)is an important basis of 文) modern mathematics,and is widely used,such as in computer science,information (Description)and communication theory,physics,and chemistry.The course Abstract Algebra is one of the main required courses for undergraduatesin mathematics.t studies the
《抽象代数》课程教学大纲 课程基本信息(Course Information) 课程代码 (Course Code) MATH 2401 *学时 (Credit Hours) 64 *学分 (Credits) 4 *课程名称 (Course Name) (中文)抽象代数 (英文)Abstract Algebra 课程类型 (Course Type) 专业必修课 授课对象 (Target Audience) 本科生 授课语言 (Language of Instruction) 中文 *开课院系 (School) 数学科学学院 先修课程 (Prerequisite) 数学分析,高等代数,初 等数论 后续课程 (post) 群与代数表示论,编码与密码,图与网络,代数数论, 代数拓扑,李群与李代数,代数几何 *课程负责人 (Instructor) 章璞 课程网址 (Course Webpage) http://math.sjtu.edu.cn/course/cxds/index.htm *课程简介(中 文) (Description) (中文 300-500 字,含课程性质、主要教学内容、课程教学目标等) “抽象代数”(通常又称为“近世代数”)是现代数学的重要基础之一,并且在计算机 科学、信息与通讯、物理、化学等领域有广泛的应用。它是高等学校数学类各专业的必修 课。这门课程研究群、环、域这三种基本的代数结构的结构理论(由于课程的时间所限,作为 本科生的抽象代数课程,一般不涉及群和环的表示理论。群表示论是本科生的另一课程;而 模论一般是研究生阶段的基础课程)。主要内容包括群的基本结构理论、置换群、群在集合 上的作用及其在计数中的应用、Sylow 定理、有限生成 Abel 群的结构、可解群的性质;环 的基本结构、中国剩余定理及其应用、环的因子分解理论、多项式环;域的扩张理论、有 限 Galois 扩张、有限域及其应用、基本的 Galois 理论及应用。通过这门课的教学,要使学 生比较熟练地掌握抽象代数的基本理论与方法,结合具体的例子理解抽象代数中的数学思 想和思维方法,使学生的抽象思维能力得到系统的训练和提高,为进一步学习数学和其它 学科奠定坚实的代数学基础。 *课程简介(英 文) (Description) (英文 300-500 字) Abstract Algebra (also called Modern Algebra) is an important basis of modern mathematics, and is widely used, such as in computer science, information and communication theory, physics, and chemistry. The course Abstract Algebra is one of the main required courses for undergraduates in mathematics. It studies the
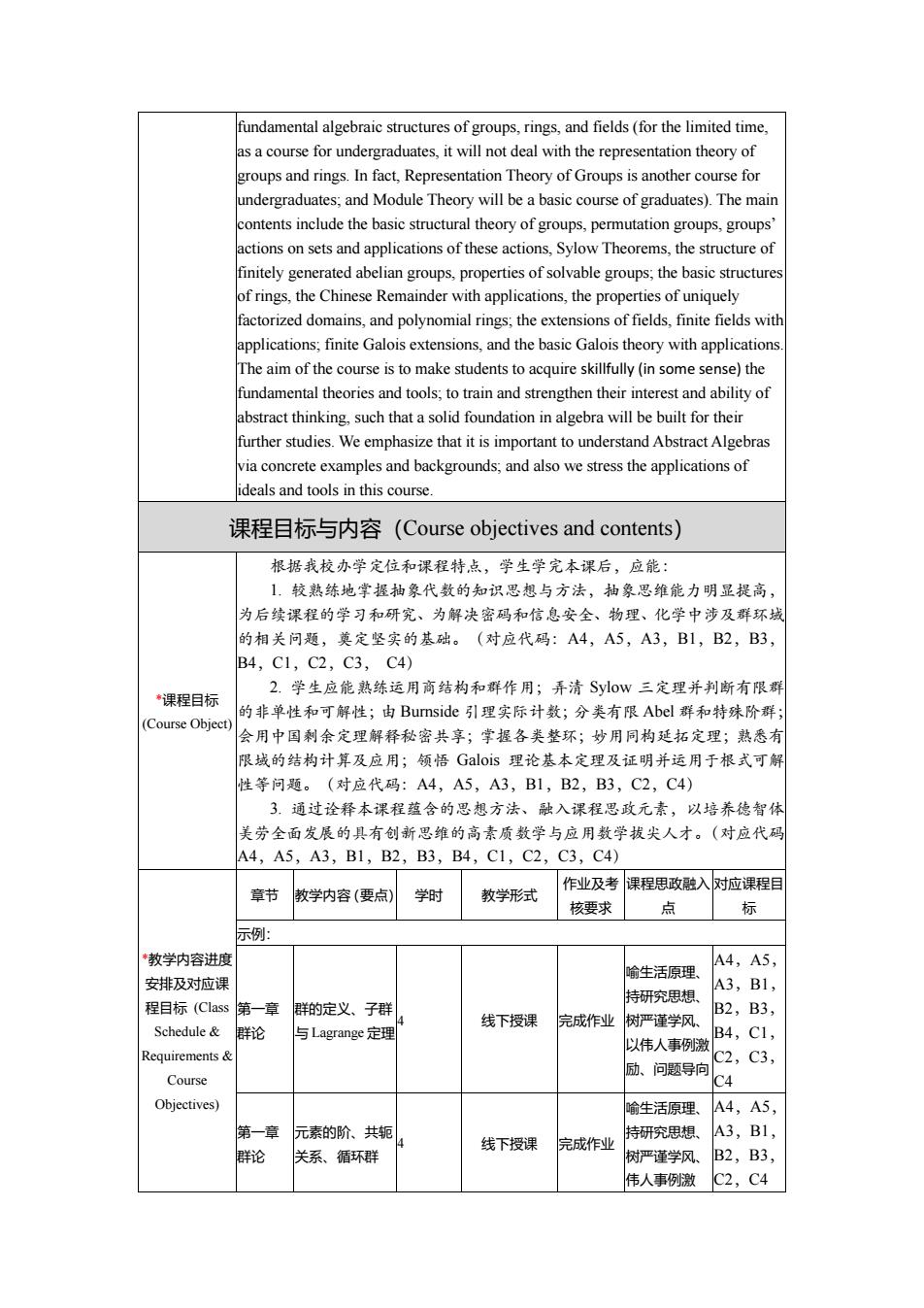
fundamental algebraic structures of groups.rings.and fields (for the limited time. groups and rings.In fact,Representation Theory of Groups is another course for undergraduates:and Module Theory will be a basic course of graduates).The mair contents include the basic structural theory of groups,permutation groups,groups' actions on sets and applications of these actions,Sylow Theorems,the structure of groups the basic structur of rings,the Chinese Rem of unique factorized domains,and polynomial rings;the extensions of fields,finite fields wit applications:finite Galois extensions.and the basic Galois theory with application The aim of the course is to make students to acquire skillfully (in some sense)the fundamental theories and tools,to train and strengthen their interest and ability of further studies.We emphasize that it is important to understand Abstract Algebras via concrete examples and backgrounds,and also we stress the applications of ideals and tools in this course. 课程目标与内容(Course objectives and contents) 根据我校办学定位和课程特点,学生学完本课后,应能: 1,较熟练地字握抽象代数的知识思想与方法,抽象思维能力明显提高 为后续课程的学习和研究、为解决蜜码和信息安全、物理、化学中涉及群环 的相关问题,莫定坚实的基础。 (对应代码:A4,A5,A3,B1,B2,B3 B4,C1,C2,C3, CA) 2.学生应能熟练运用商结构和群作用:弄清SyoW三定理并判断有限无 课程目标 的非单性和可解性;由Burnside引理实际计数;分类有限Abel群和特殊阶群 (Course Object 会用中国刺余定理解释秘密共享:掌提各类整环:妙用同柏延拓定理:熟悉 限域的结构计算及应用;领悟Galois理论基本定理及证明并运用于根式可 性等问题。(对应代码:A4,A5,A3,B1,B2,B3,C2,C4) 3.通过诠释本课程蕴含的思想方法、融入课程思政元素,以培养德智佛 美劳全面发展的具有创新思维的高素质数学与应用数学拔尖人才。(对应代码 A4,A5,A3,B1,B2,B3,B4,C1,C2,C3,C4) 章节 教学内容(要点) 学时 教学形式 作业及考课程思政融入时应课程目 核要求 点 标 示例 教学内容讲电 喻生活原理 A4,A5 安排及对应课 特研究思无 BI 程目标(Clas 群的定义、子群 线下授课 完成作 树严谨学风 B2,B3, Schedule&群论 与Lagrange定理 以伟人事5储 B4,C1, Requirements 励.问题导向 C2,C3, Course Objectives) 啥生活原理 第一章 元索的阶、共轭 特研究思想 完成作 A3,B1 群论 线下授课 关系、循环群 亚节学风 B2,B3, 伟人事例激 C2,C4
fundamental algebraic structures of groups, rings, and fields (for the limited time, as a course for undergraduates, it will not deal with the representation theory of groups and rings. In fact, Representation Theory of Groups is another course for undergraduates; and Module Theory will be a basic course of graduates). The main contents include the basic structural theory of groups, permutation groups, groups’ actions on sets and applications of these actions, Sylow Theorems, the structure of finitely generated abelian groups, properties of solvable groups; the basic structures of rings, the Chinese Remainder with applications, the properties of uniquely factorized domains, and polynomial rings; the extensions of fields, finite fields with applications; finite Galois extensions, and the basic Galois theory with applications. The aim of the course is to make students to acquire skillfully (in some sense) the fundamental theories and tools; to train and strengthen their interest and ability of abstract thinking, such that a solid foundation in algebra will be built for their further studies. We emphasize that it is important to understand Abstract Algebras via concrete examples and backgrounds; and also we stress the applications of ideals and tools in this course. 课程目标与内容(Course objectives and contents) *课程目标 (Course Object) 根据我校办学定位和课程特点,学生学完本课后,应能: 1. 较熟练地掌握抽象代数的知识思想与方法,抽象思维能力明显提高, 为后续课程的学习和研究、为解决密码和信息安全、物理、化学中涉及群环域 的相关问题,奠定坚实的基础。(对应代码:A4,A5,A3,B1,B2,B3, B4,C1,C2,C3, C4) 2. 学生应能熟练运用商结构和群作用;弄清 Sylow 三定理并判断有限群 的非单性和可解性;由 Burnside 引理实际计数;分类有限 Abel 群和特殊阶群; 会用中国剩余定理解释秘密共享;掌握各类整环;妙用同构延拓定理;熟悉有 限域的结构计算及应用;领悟 Galois 理论基本定理及证明并运用于根式可解 性等问题。(对应代码:A4,A5,A3,B1,B2,B3,C2,C4) 3. 通过诠释本课程蕴含的思想方法、融入课程思政元素,以培养德智体 美劳全面发展的具有创新思维的高素质数学与应用数学拔尖人才。(对应代码 A4,A5,A3,B1,B2,B3,B4,C1,C2,C3,C4) *教学内容进度 安排及对应课 程目标 (Class Schedule & Requirements & Course Objectives) 章节 教学内容(要点) 学时 教学形式 作业及考 核要求 课程思政融入 点 对应课程目 标 示例: 第一章 群论 群的定义、子群 与 Lagrange 定理 4 线下授课 完成作业 喻生活原理、 持研究思想、 树严谨学风、 以伟人事例激 励、问题导向 A4,A5, A3,B1, B2,B3, B4,C1, C2,C3, C4 第一章 群论 元素的阶、共轭 关系、循环群 4 线下授课 完成作业 喻生活原理、 持研究思想、 树严谨学风、 伟人事例激 A4,A5, A3,B1, B2,B3, C2,C4

励、问题导向 喻生活原理, 正规子群、商群 持研究思想 A4,A5 第一章 群同态其木宗 线下授课 完成作业 A3,B1 亚节学风 群论 B2,B3, 理、置换群 以伟人 励、问题导向 C2,C4 喻生活原理 群在集合上的作 特研究思想 A4,A5 器论 用、项问题, 线下授课 A3,B1 完成作业树严谨学风 B2 B3 Sylow定理 以伟人 、问题 2,C4 喻生活原理 Sylow定理 A4,A5 持严究用相 第一章 群论 (续)、群的直 线下授课 A3,B1 完成作业严学风 C4 励、问题导 除生活原理 A4,A5 群的生成元与定 特研究思想 第一言 群论 义关系有限 线下授 完成作业 树严谨学 3.B1 AbeI群 以伟人事 励、问题导年 喻生活原理、 完成作业 A4,A5 第一章 小N阶群的结构 线下授课 大作业, 3.B1 群论 可解群 中考试。 人伟人事份 2 书报告 励、问题导向 C2,C4 喻生活原理 第 环的概念、无 因子环的特征、 线下授课 完成作 以伟人事例味 环同态基本定理 B2,B3 激励、以问题 C2,C4 为导向 整环的商域、环 喻生活原珥 持研究思想 第二的直和、中国剩 B2,B3, 环论 余定理、极大理 线下授课 完成作业树严谨学风、 B4,C1, 以伟人事例 想和嘉理想 问题导向 2.C3 喻生活原理 特研究思相 A4,A5 第二章唯一因子分解 线下授课 A3,B1, 环论 完成作业树严谨学风 环、主理想整环 B2,B3, 以伟人事 应、问题导向 2,C4
励、问题导向 第一章 群论 正规子群、商群、 群同态基本定 理、置换群 4 线下授课 完成作业 喻生活原理、 持研究思想、 树严谨学风、 以伟人事例激 励、问题导向 A4,A5, A3,B1, B2,B3, C2,C4 第一章 群论 群在集合上的作 用、项链问题、 Sylow 定理 4 线下授课 完成作业 喻生活原理、 持研究思想、 树严谨学风、 以伟人事例激 励、问题导向 A4,A5, A3,B1, B2,B3, C2,C4 第一章 群论 Sylow 定理 (续)、群的直 积 4 线下授课 完成作业 喻生活原理、 持研究思想、 树严谨学风、 以伟人事例激 励、问题导向 A4,A5, A3,B1, B2,B3, C2,C4 第一章 群论 群的生成元与定 义关系、有限 Abel 群 4 线下授课 完成作业 喻生活原理、 持研究思想、 树严谨学风、 以伟人事例激 励、问题导向 A4,A5, A3,B1, B2,B3, C2,C4 第一章 群论 小阶群的结构、 可解群 4 线下授课 完成作业、 大作业、期 中考试、读 书报告 喻生活原理、 持研究思想、 树严谨学风、 以伟人事例激 励、问题导向 A4,A5, A3,B1, B2,B3, C2,C4 第二章 环论 环的概念、无零 因子环的特征、 环同态基本定理 4 线下授课 完成作业 喻生活原理、 持研究思想、 树严谨学风、 以伟人事例相 激励、以问题 为导向 A4,A5, A3,B1, B2,B3, C2,C4 第二章 环论 整环的商域、环 的直和、中国剩 余定理、极大理 想和素理想、 4 线下授课 完成作业 喻生活原理、 持研究思想、 树严谨学风、 以伟人事例激 励、问题导向 A4,A5, A3,B1, B2,B3, B4,C1, C2,C3, C4 第二章 环论 唯 一 因 子 分 解 环、主理想整环 4 线下授课 完成作业 喻生活原理、 持研究思想、 树严谨学风、 以伟人事例激 励、问题导向 A4,A5, A3,B1, B2,B3, C2,C4
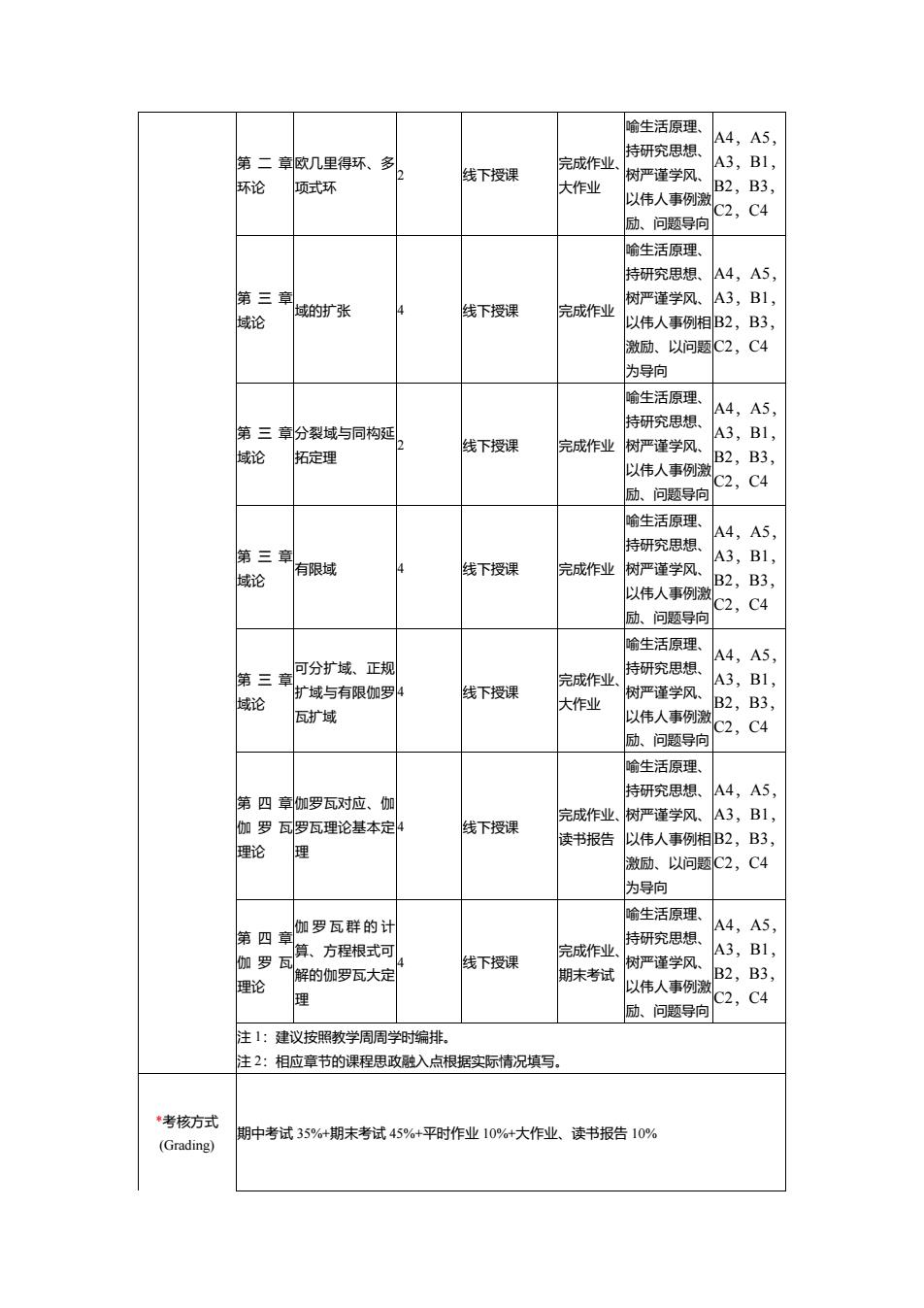
喻生活原理 饮几里得环、多 成作业 诗研究思想 A4.A5 环论 线下授课 3 项式环 大作业 以伟人事例 2, 励。问颗导店 金生活原理 持研究思想】 A5 第三到 树严谨学风 域的扩张 线下授课 完成作 3, 域论 以伟人事例 B2,B3, 微励、以问题C2,C4 为向 喻生活原理 持研究思想 A4,A5 第三到分裂域与同构延 线下授课 完成作业树严谨学风 A3,B1, 域论 拓定理 B2,B3, 以伟人事例 2.C4 励、问题导向 喻生活原理 A4,A5 特研究思想 第三章到 域论 有限域 线下授课 A3,B1 完成作业树严谨学风 B2,B3 以伟人事 励、问题导立 C2,C4 喻生活原理 A4.A5 可分扩域、正规 特开究用相 第三草 完成作业 A3,B1 域论 扩域与有限和罗 线下授课 树严谨学风 瓦扩域 大作业 B2,B3, 伟人 、问题号断 C2,C4 喻生活原理 持开究甲相 A4,A5 第四音加罗瓦对应、加 罗 完成作业.树严谨学风 A3.B1 罗瓦理论基本定 线下授课 读书报告 伟人事伤 B3 理论 激动、以问片 C 为导向 罗瓦群的 喻生活原理 第四章 A4.A5 持研究思想」 伽罗 算、方程根式 线下授课 成作业 解的加罗瓦大元 期末考 B3 理论 以伟人事例 2,C4 励、问题导向 注1:建议按昭教学周周学综 相应章 果程 点根据实标情况填写 *考核方式 (Grading) 期中考试35%+期未考试45%+平时作业10%+大作业、读书报告10%
第二章 环论 欧几里得环、多 项式环 2 线下授课 完成作业、 大作业 喻生活原理、 持研究思想、 树严谨学风、 以伟人事例激 励、问题导向 A4,A5, A3,B1, B2,B3, C2,C4 第三章 域论 域的扩张 4 线下授课 完成作业 喻生活原理、 持研究思想、 树严谨学风、 以伟人事例相 激励、以问题 为导向 A4,A5, A3,B1, B2,B3, C2,C4 第三章 域论 分裂域与同构延 拓定理 2 线下授课 完成作业 喻生活原理、 持研究思想、 树严谨学风、 以伟人事例激 励、问题导向 A4,A5, A3,B1, B2,B3, C2,C4 第三章 域论 有限域 4 线下授课 完成作业 喻生活原理、 持研究思想、 树严谨学风、 以伟人事例激 励、问题导向 A4,A5, A3,B1, B2,B3, C2,C4 第三章 域论 可分扩域、正规 扩域与有限伽罗 瓦扩域 4 线下授课 完成作业、 大作业 喻生活原理、 持研究思想、 树严谨学风、 以伟人事例激 励、问题导向 A4,A5, A3,B1, B2,B3, C2,C4 第四章 伽罗瓦 理论 伽罗瓦对应、伽 罗瓦理论基本定 理 4 线下授课 完成作业、 读书报告 喻生活原理、 持研究思想、 树严谨学风、 以伟人事例相 激励、以问题 为导向 A4,A5, A3,B1, B2,B3, C2,C4 第四章 伽罗瓦 理论 伽 罗 瓦 群 的 计 算、方程根式可 解的伽罗瓦大定 理 4 线下授课 完成作业、 期末考试 喻生活原理、 持研究思想、 树严谨学风、 以伟人事例激 励、问题导向 A4,A5, A3,B1, B2,B3, C2,C4 注 1:建议按照教学周周学时编排。 注 2:相应章节的课程思政融入点根据实际情况填写。 *考核方式 (Grading) 期中考试 35%+期末考试 45%+平时作业 10%+大作业、读书报告 10%

教材或卷考资1.《近世代数引论》,冯克勤、李尚志、章瑰,中国科学技术大学出版社,2018 料(Tbo0ks(第4版).心十二五”国家重点图书;“中国科学院指定考研参考书") &Other 如罗瓦理 论天才的澈情》,章璞,现代数学慕础37,高等教有出版社 Materials))2016第二次印. 其它(Mor©)本大钢适应于荣苓课程。 备注(Notes) 与本课程关联较多的后续课程有:群与代数表示论,编码与密码,图与网 路,代数数论,代数拓扑,李群与李代数,代数几何等 备注说明: 1带内空为必填师 2.课程简介字数为300500字:课程大纲以表述清楚教学安排为宜,字数不限
*教材或参考资 料 (Textbooks & Other Materials) 1. 《近世代数引论》,冯克勤、李尚志、章璞, 中国科学技术大学出版社,2018 (第 4 版). (“十二五”国家重点图书;“中国科学院指定考研参考书") 2. 《伽罗瓦理论-天才的激情》,章璞,现代数学基础 37,高等教育出版社, 2016 第二次印刷. 其它(More) 本大纲适应于荣誉课程。 备注(Notes) 与本课程关联较多的后续课程有:群与代数表示论,编码与密码,图与网 络,代数数论,代数拓扑,李群与李代数,代数几何等 备注说明: 1.带*内容为必填项。 2.课程简介字数为 300-500 字;课程大纲以表述清楚教学安排为宜,字数不限