《代数几何》课程教学大纲 课程基本信息(Course Information) 课程代码 *学时 MATH3609 学分 (Course Code (Credits *课程名称 (中文)代数几何 (Course Name) (英文)Algebraic Geometry 课程类型 (Cour 业方向选修课 Type) 授课对象 (Target 本科生 Audience 授课语言 (Language of 中文 Instruction 开课院系 数学科学学院 (School) 先修误程 后续课 (Prerequis 抽象代数,交换代数基 ite) (post) 程网 *课程负责人 址 (Instructo张光连 (Cours r) 这是为本科生准备的一个学期的课程。在不假定具有很多的交换代数背景之 下,我们都给一个完整的证明。关于代数簇,我们是取白于BmD「2]和 课得简个 (中文) 个环层空间,它局部同构于 个域上的仿射代数簇 (Descripti 尽管我们没有讨论概型 但是两者之间的转换不是太困难的。 章是关 交换代数的准备知识,第二与三章讨论一般维数的代数筷,第四章是讨论一到 on) 的代数簇(即代数曲线)的Riemann--Roch定理。在本课程中,通常我们都是 考虑代数闭域上的不可约代数族,我们不讨论有限域的情况。 *课程简介 The aim is to make this a text that can be used in one semester at undergraduate (英文) evel.I have tried to give complete proofs without assuming a background in (Descript algebra at the level.The point of view here is that of Bump[2]or Chapter Iof Mumford[3]-a variety is a ringed space locally isomorphic to an affine variety ove on) a field.AlthoughIdo not treat schemesI trust the reader will not find the
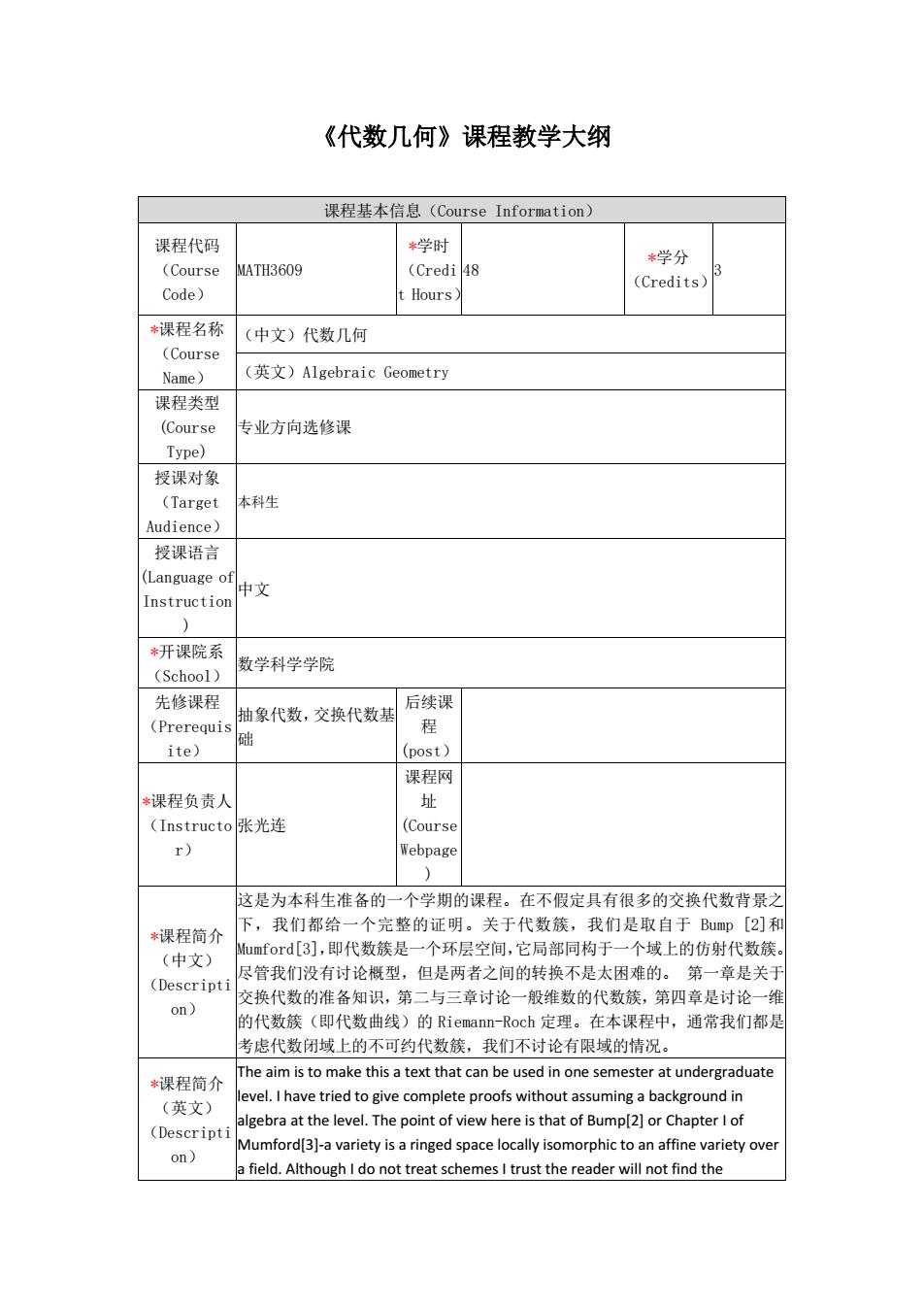
《代数几何》课程教学大纲 课程基本信息(Course Information) 课程代码 (Course Code) MATH3609 *学时 (Credi t Hours) 48 *学分 (Credits) 3 *课程名称 (Course Name) (中文)代数几何 (英文)Algebraic Geometry 课程类型 (Course Type) 专业方向选修课 授课对象 (Target Audience) 本科生 授课语言 (Language of Instruction ) 中文 *开课院系 (School) 数学科学学院 先修课程 (Prerequis ite) 抽象代数,交换代数基 础 后续课 程 (post) *课程负责人 (Instructo r) 张光连 课程网 址 (Course Webpage ) *课程简介 (中文) (Descripti on) 这是为本科生准备的一个学期的课程。在不假定具有很多的交换代数背景之 下,我们都给一个完整的证明。关于代数簇,我们是取自于 Bump [2]和 Mumford[3],即代数簇是一个环层空间,它局部同构于一个域上的仿射代数簇。 尽管我们没有讨论概型,但是两者之间的转换不是太困难的。 第一章是关于 交换代数的准备知识,第二与三章讨论一般维数的代数簇,第四章是讨论一维 的代数簇(即代数曲线)的 Riemann-Roch 定理。在本课程中,通常我们都是 考虑代数闭域上的不可约代数簇,我们不讨论有限域的情况。 *课程简介 (英文) (Descripti on) The aim is to make this a text that can be used in one semester at undergraduate level. I have tried to give complete proofs without assuming a background in algebra at the level. The point of view here is that of Bump[2] or Chapter I of Mumford[3]-a variety is a ringed space locally isomorphic to an affine variety over a field. Although I do not treat schemes I trust the reader will not find the
transition too difficult. The first chapter is mainly about the preparation ofcommutative agebra,the chapter 2 and chapter 3contain material applicable to varieties of every dimension,the last chapter contain material which is particular to the theory of curves.We give an introduction on Riemann-Roch theorem of a curve.In this course.I only consider irreducible varieties over an algebraically closed field,not work over a finite field. 课程目标与内容(Course objectives and contents) 1.了解代数几何的基本思想与方法(A3)。 *课程目标 掌握仿射代数簇的基本理论, 了解代数曲线的Riemann-Roch定理(A5) 通过教学,培养学生发现问题与解决问题的能力(B2,C2),利用大作 (Course Obiect) 与课堂汇报的方式培养学生团队协作利用代数几何解决问愿的能力(A5,B3 C1)。 作业及 章节散学内容(要点) 学时 教学形式考核要 课程思政融对应课程 入点 目标 求 课后作 1.1 Noether环与理 想的准素分解 课堂教学 业,独立真与美 3,B1,C 完成 *教学内容湖 度安排及对 应课程目标 整性与Noether 课后作 A3.BI B2 (Class 2 正规化定理 课堂教学 业,独立标准化思想 Schedule& 完成 Requireme s&Course .3 Hilbert零点定 课后作 课堂教学 业,独立 代数与几何A3,B1,B2 Objectives 完成 相容 定义与Zariski A3,B1,B2 2.1 拓扑 课堂教学 课后们形式化公理 业,独立 完成 体系的应用,C1 Noether空间 课堂教学 独立 几何与代数A3,B1,2 相容 完成 2.3 坐标环与占的讲 课后 创新与发A3.A4.B1 2.4 步刻画与态射 课堂教学 完 独斗性思维 B4,C3 3.1 Extension定理 课堂教学 课后作附整体处理方 A3,BI,CI
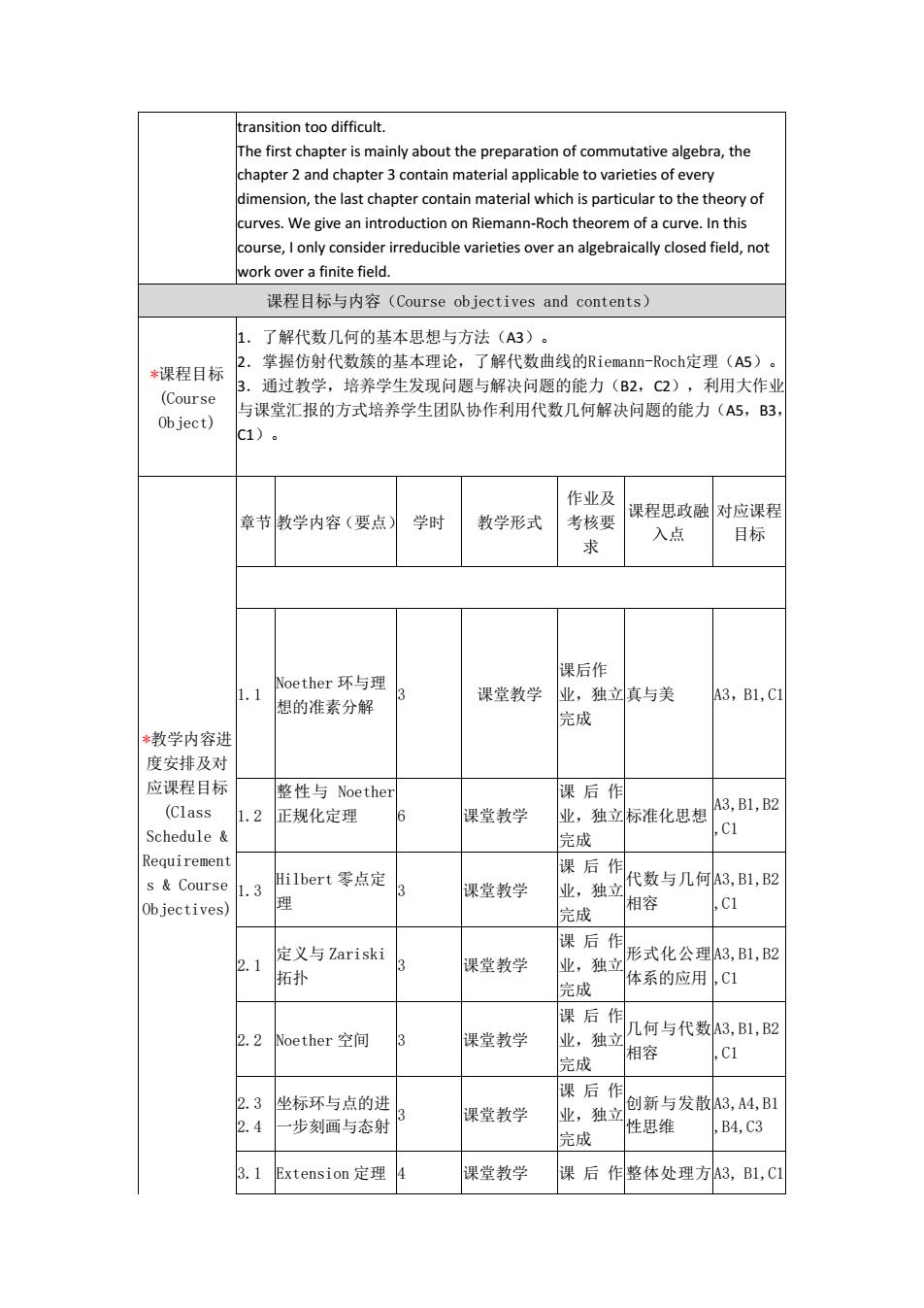
transition too difficult. The first chapter is mainly about the preparation of commutative algebra, the chapter 2 and chapter 3 contain material applicable to varieties of every dimension, the last chapter contain material which is particular to the theory of curves. We give an introduction on Riemann-Roch theorem of a curve. In this course, I only consider irreducible varieties over an algebraically closed field, not work over a finite field. 课程目标与内容(Course objectives and contents) *课程目标 (Course Object) 1.了解代数几何的基本思想与方法(A3)。 2.掌握仿射代数簇的基本理论,了解代数曲线的Riemann-Roch定理(A5)。 3.通过教学,培养学生发现问题与解决问题的能力(B2,C2),利用大作业 与课堂汇报的方式培养学生团队协作利用代数几何解决问题的能力(A5,B3, C1)。 *教学内容进 度安排及对 应课程目标 (Class Schedule & Requirement s & Course Objectives) 章节 教学内容(要点) 学时 教学形式 作业及 考核要 求 课程思政融 入点 对应课程 目标 1.1 Noether 环与理 想的准素分解 3 课堂教学 课后作 业,独立 完成 真与美 A3,B1,C1 1.2 整性与 Noether 正规化定理 6 课堂教学 课后作 业,独立 完成 标准化思想 A3,B1,B2 ,C1 1.3 Hilbert 零点定 理 3 课堂教学 课后作 业,独立 完成 代数与几何 相容 A3,B1,B2 ,C1 2.1 定义与 Zariski 拓扑 3 课堂教学 课后作 业,独立 完成 形式化公理 体系的应用 A3,B1,B2 ,C1 2.2 Noether 空间 3 课堂教学 课后作 业,独立 完成 几何与代数 相容 A3,B1,B2 ,C1 2.3 2.4 坐标环与点的进 一步刻画与态射 3 课堂教学 课后作 业,独立 完成 创新与发散 性思维 A3,A4,B1 ,B4,C3 3.1 Extension 定理 4 课堂教学 课后作整体处理方A3, B1,C1
业,独立法 成 3.2 Going-up定理与 课后作 Going-down定理1 棵堂教学 业,独立真与美 A3, B1,B2,C1 完成 Krull主理想定 后 作 3.3理与超曲面的维 课堂教学 几何与代裁 A3,BI,B2 业,独立 完成 相容 课后作 交的维数与完全 果堂教学 业 几何与代数A3,B1,B2 .4 交理论 完成 课后作 相对维数的半连 几何与代数A3,B1,B2 8.5 续定理 课堂教学 业,独斗相容 切空间与奇点理 3.6 课堂教学 课后作几何与代数3,B1,2 业,独立 论 相容 C1 宗成 课后付 4.1射影代数族 课堂教学 业,独立真与美 3,BI,B2 完成 4.2除子与亏格与 课后作经典间题上 n-Roch定 课堂教学 独立 新思想的础 3,B1,B2 4.3理介 完成 撞 *者核方式 大作业(60分)+课堂报告(40分) (Grading) .M.FAtyah and I.GMacDonald,Commuative Algebra The advanced book rogram,1969 ◆教材或参考资 2.Daniel Bump.Algebraic Gcometry.World Scientific.1998. 料Texthooks 3.D.Mumford.The Red book of varieties and schemes.Lecture notes in Mathematics 1358. &Other als Springer-Verlag(1988). P.Serre, Ann.0 f Math..61(1955,197-278 Guanglian Zhang.Lectures on Algebraic Geometry. 其它(More) 备注(Notes)
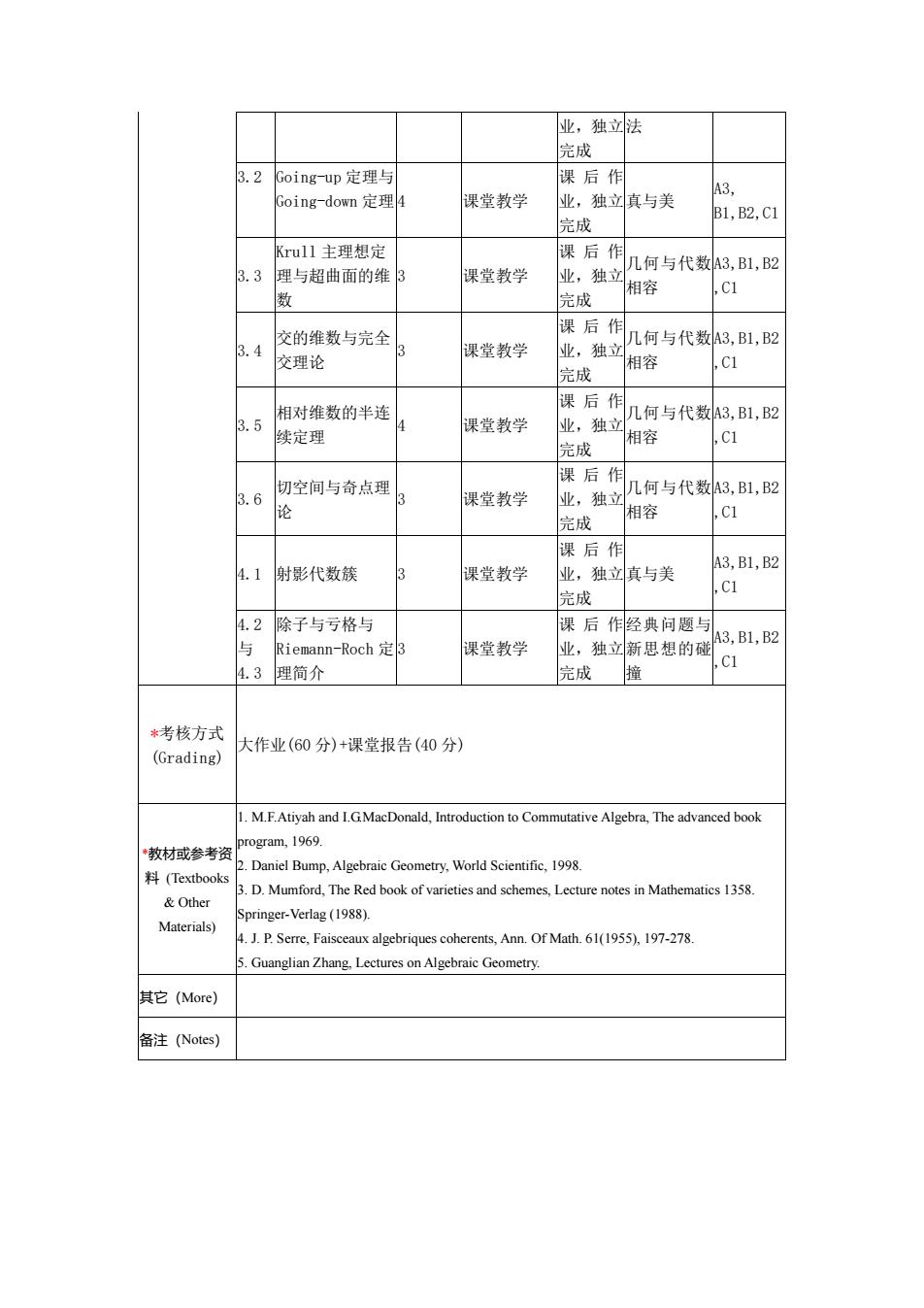
业,独立 完成 法 3.2 Going-up 定理与 Going-down 定理 4 课堂教学 课后作 业,独立 完成 真与美 A3, B1,B2,C1 3.3 Krull 主理想定 理与超曲面的维 数 3 课堂教学 课后作 业,独立 完成 几何与代数 相容 A3,B1,B2 ,C1 3.4 交的维数与完全 交理论 3 课堂教学 课后作 业,独立 完成 几何与代数 相容 A3,B1,B2 ,C1 3.5 相对维数的半连 续定理 4 课堂教学 课后作 业,独立 完成 几何与代数 相容 A3,B1,B2 ,C1 3.6 切空间与奇点理 论 3 课堂教学 课后作 业,独立 完成 几何与代数 相容 A3,B1,B2 ,C1 4.1 射影代数簇 3 课堂教学 课后作 业,独立 完成 真与美 A3,B1,B2 ,C1 4.2 与 4.3 除子与亏格与 Riemann-Roch 定 理简介 3 课堂教学 课后作 业,独立 完成 经典问题与 新思想的碰 撞 A3,B1,B2 ,C1 *考核方式 (Grading) 大作业(60 分)+课堂报告(40 分) *教材或参考资 料 (Textbooks & Other Materials) 1. M.F.Atiyah and I.G.MacDonald, Introduction to Commutative Algebra, The advanced book program, 1969. 2. Daniel Bump, Algebraic Geometry, World Scientific, 1998. 3. D. Mumford, The Red book of varieties and schemes, Lecture notes in Mathematics 1358. Springer-Verlag (1988). 4. J. P. Serre, Faisceaux algebriques coherents, Ann. Of Math. 61(1955), 197-278. 5. Guanglian Zhang, Lectures on Algebraic Geometry. 其它(More) 备注(Notes)

备注说明: 1.带内容为必填项, 2.课程简介字数为30-500字:课程大纲以表述清楚教学安排为宜,字数不限
备注说明: 1.带*内容为必填项。 2.课程简介字数为 300-500 字;课程大纲以表述清楚教学安排为宜,字数不限