《动力系统》课程教学大纲 课程基本信息(Course Information) 学时 课程代码 MATH3502 (Course Cod Hours) *课程名称 (中文)动力系统 (Course Name) (英文)Dynamical Systems 课程类型 专业方向选修 (Course Type) 授课对橡 (Target 本科生 Audience) 授课语言 (Language of全中文 Instruction) *开课院系 数学科学学院 (School) 先修课程数学分析、线性代数、常后续课程 (Prerequisite)微分方程、基础拓扑学 (post) *课程负责人 课程网址 肖冬梅、王晓东 (Course (Instructor) Webpage) (中文300.S00字,含棵程性质丰要教学内容课程教学目标等) 的重要分支,本课程主要介绍(实)动力系统的基本理论,涉及到维(区 +课程简介(中间或圆周上)动力系统,如Sakovskii定理、L-小Yok混沌、圆周同胚的性质及旋转数等 ) 高维动力系统主要介绍驭曲性理论,包括取曲线性同构的性质、双曲不动点及双曲性在扰 (Description)动下的保持、双曲不动点的局部稳定流形等;另外会介铅一些动力系统中的经典例子,如 Logistic映射、符号动力系统Smale马蹄.Anosov环而同构等, (英文300-500字) Dynamical systems is an important branch in mathematics.This course is devoted to introduce basic theories of (real)dynamical systems.For one-dimensional dynamics (ie.dynamics on ar i课程简介(英,it contains Sarkovski Theorem Li-York chaos, (Description) utomorphisms,robustness of hyperbolic fixed points and hyperbolicity under perturbations ocastable manifold of hyperbolic fixed pointset.ome assicaexameof dynamical systems would also be introduced.for instance.the Logistic map.symbolic dynamical systems ,Anosov automorphism ontorus,t
《动力系统》课程教学大纲 课程基本信息(Course Information) 课程代码 (Course Code) MATH3502 *学时 (Credit Hours) 48 *学分 (Credits) 3 *课程名称 (Course Name) (中文)动力系统 (英文)Dynamical Systems 课程类型 (Course Type) 专业方向选修 授课对象 (Target Audience) 本科生 授课语言 (Language of Instruction) 全中文 *开课院系 (School) 数学科学学院 先修课程 (Prerequisite) 数学分析、线性代数、常 微分方程、基础拓扑学 后续课程 (post) *课程负责人 (Instructor) 肖冬梅、王晓东 课程网址 (Course Webpage) *课程简介(中 文) (Description) (中文 300-500 字,含课程性质、主要教学内容、课程教学目标等) 动力系统是数学的重要分支,本课程主要介绍(实)动力系统的基本理论,涉及到一维(区 间或圆周上)动力系统,如 Sakovskii 定理、Li-York 混沌、圆周同胚的性质及旋转数等; 高维动力系统主要介绍双曲性理论,包括双曲线性同构的性质、双曲不动点及双曲性在扰 动下的保持、双曲不动点的局部稳定流形等;另外会介绍一些动力系统中的经典例子,如 Logistic 映射、符号动力系统、Smale 马蹄、Anosov 环面同构等。 *课程简介(英 文) (Description) (英文 300-500 字) Dynamical systems is an important branch in mathematics. This course is devoted to introduce basic theories of (real) dynamical systems. For one-dimensional dynamics (i.e. dynamics on an interval or an circle), it contains Sarkovskii Theorem, Li-York chaos, circle homeomorphisms and rotation numbers, etc. For higher dimensional dynamics, it contains hyperbolic linear automorphisms, robustness of hyperbolic fixed points and hyperbolicity under perturbations, local stable manifold of hyperbolic fixed points, etc. Some classical examples of dynamical systems would also be introduced, for instance, the Logistic map, symbolic dynamical systems, Smale’s horseshoe, Anosov automorphism on torus, etc
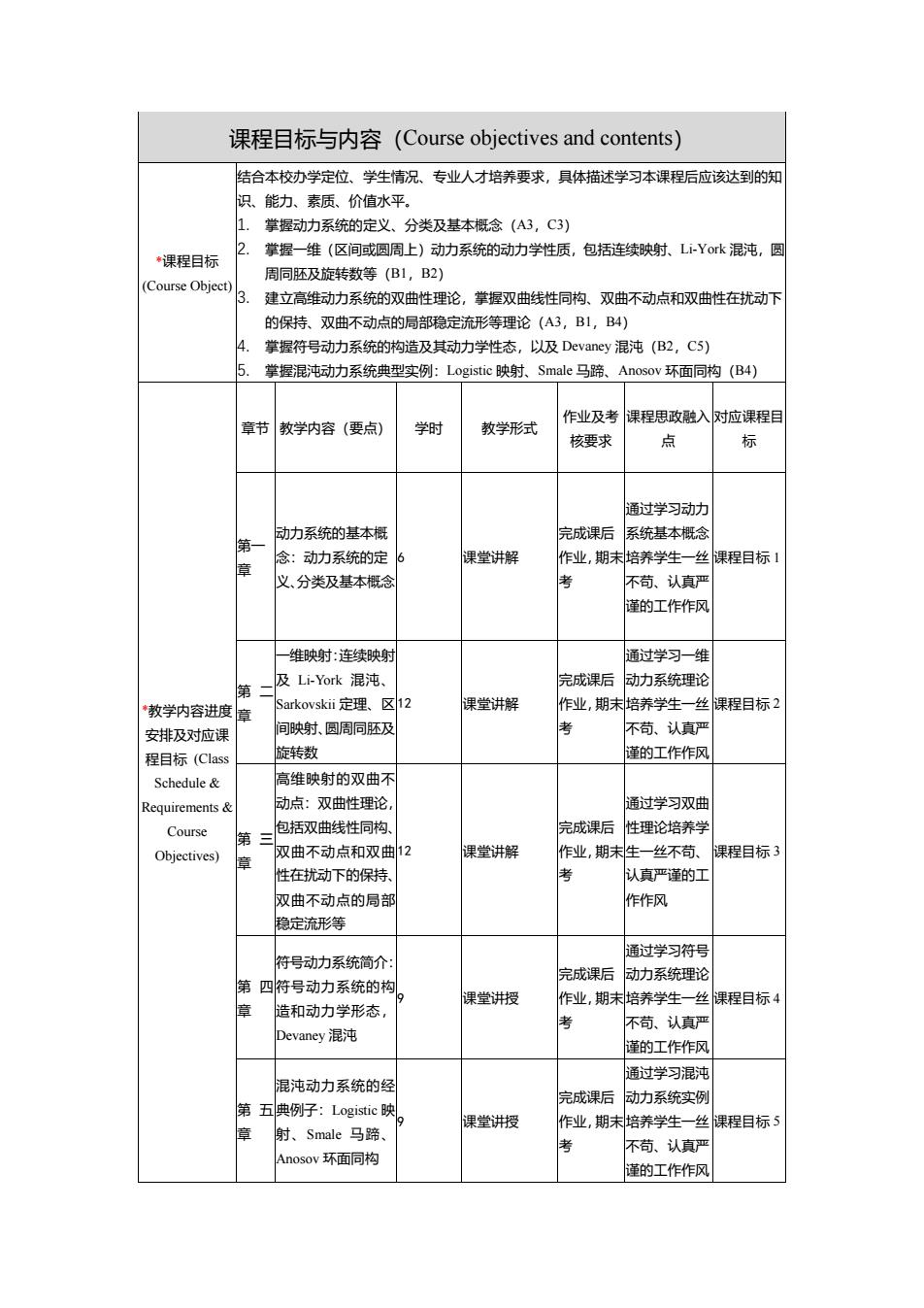
课程目标与内容(Course objectives and contents) 结合本校办学定位、学生情况、专业人才培养要求,具体描述学习本课程后应该达到的灯 识、能力、素质、价值水平. 1.掌握动力系统的定义、分类及基本凝念(A3,C3) 课程目标 掌据一维(区间或圆周上)动力系统的动力学性质,包括连续缺射、L-Yk混沌,圆 周同胚及旋转数等(B1,B2) (Course Object) 建立高维动力系统的双曲性理论,掌握双曲线性同构、双曲不动点和双曲性在扰动下 的保持、双曲不动点的局部稳定流形等理论(A3,BL,B4) 4. 掌据符号动力系统的构造及其动力学性态,以及Devaney混沌(B2,C5) 掌握泥沌动力系统典型实例:Logistic映射、Smale马蹄、Anosov环面同构(B4) 作业及老 章节教学内容(要点) 学时 救学形式 核要求 点 通过学习动 第 动力系统的基本概 完成果后系统基本概会 念:动力系统的定 课堂讲解 作业,期未培养学生一丝棵程目标 义分类及基本据冷 不苟.认京严 逢的工作作 一维映射:连续映的 通过学习一维 及Li-York混沌, 完成课后动力系统理论 教学内容进度章 课堂讲解 作业,期末培养学生一丝课程目标, 安排及对应课 间映射周同还及 不简、认真 程目标Clas 旋转数 谨的工作作顶 Schedule& 高维映射的双曲不 Requirements 动点:双曲性理论 通过学习双曲 Course 包括双曲线性同构 完成课后 性理论培养 Obiectives) 曲不动点和双 课堂讲解 作业,期未性一丝不苟 果程目标 性在扰动下的保持 认真严谨的口 双曲不动点的局部 作作风 稳定流形等 符号动力系统简 通过学习符号 完成课后 第四符号动力系统的构 动力系统理 课堂讲授 作业,期末培养学生一 课程目标 章 浩和动力学形态 不苟.认直 Devaney混沌 详的工作作重 混沌动力系统的 通过学习混 第五典例子:Logistie映 完成课后 动力系统实伤 课堂讲授 作业,期未培养学生一丝 课程目标 射、smac马蹄、 不苟认直严 Ansov环面同构 的工作作风
课程目标与内容(Course objectives and contents) *课程目标 (Course Object) 结合本校办学定位、学生情况、专业人才培养要求,具体描述学习本课程后应该达到的知 识、能力、素质、价值水平。 1. 掌握动力系统的定义、分类及基本概念(A3,C3) 2. 掌握一维(区间或圆周上)动力系统的动力学性质,包括连续映射、Li-York 混沌,圆 周同胚及旋转数等(B1,B2) 3. 建立高维动力系统的双曲性理论,掌握双曲线性同构、双曲不动点和双曲性在扰动下 的保持、双曲不动点的局部稳定流形等理论(A3,B1,B4) 4. 掌握符号动力系统的构造及其动力学性态,以及 Devaney 混沌(B2,C5) 5. 掌握混沌动力系统典型实例:Logistic 映射、Smale 马蹄、Anosov 环面同构(B4) *教学内容进度 安排及对应课 程目标 (Class Schedule & Requirements & Course Objectives) 章节 教学内容(要点) 学时 教学形式 作业及考 核要求 课程思政融入 点 对应课程目 标 第一 章 动力系统的基本概 念:动力系统的定 义、分类及基本概念 6 课堂讲解 完成课后 作业,期末 考 通过学习动力 系统基本概念 培养学生一丝 不苟、认真严 谨的工作作风 课程目标 1 第 二 章 一维映射:连续映射 及 Li-York 混沌、 Sarkovskii 定理、区 间映射、圆周同胚及 旋转数 12 课堂讲解 完成课后 作业,期末 考 通过学习一维 动力系统理论 培养学生一丝 不苟、认真严 谨的工作作风 课程目标 2 第 三 章 高维映射的双曲不 动点:双曲性理论, 包括双曲线性同构、 双曲不动点和双曲 性在扰动下的保持、 双曲不动点的局部 稳定流形等 12 课堂讲解 完成课后 作业,期末 考 通过学习双曲 性理论培养学 生一丝不苟、 认真严谨的工 作作风 课程目标 3 第 四 章 符号动力系统简介: 符号动力系统的构 造和动力学形态, Devaney 混沌 9 课堂讲授 完成课后 作业,期末 考 通过学习符号 动力系统理论 培养学生一丝 不苟、认真严 谨的工作作风 课程目标 4 第 五 章 混沌动力系统的经 典例子:Logistic 映 射、Smale 马蹄、 Anosov 环面同构 9 课堂讲授 完成课后 作业,期末 考 通过学习混沌 动力系统实例 培养学生一丝 不苟、认真严 谨的工作作风 课程目标 5

注1:建议按昭教学周周学时编推 注2:相应章节的课程思政融入点根据实际情况填与, *考核方式(1】平时作到业40分 (Grading) (2)期末考试60分 “教材或参考资1.《微分动力系统》,文兰著,高等教育出版社,2015. 料(Tcx 《微分动力系统原理》,张筑生著,科学出版社,1987,200 Other Differential Equations,Dynamical Systems-An introductin to Chaos(Second Edition). Materials) Morris W.Hirsch.Stephen Smale,Robert LDevaney,2007. 其它(Mo©)课程大部分内容来自于教材1的前三章,教材2的前三章,教材3的第15章。 备注(Notes) 备注说明: 1.带内容为必填项。 2.课程简介字数为300500字:课程大纲以表述清楚教学安排为宜,字数不限
注 1:建议按照教学周周学时编排。 注 2:相应章节的课程思政融入点根据实际情况填写。 *考核方式 (Grading) (1)平时作业 40 分 (2)期末考试 60 分 *教材或参考资 料 (Textbooks & Other Materials) 1.《微分动力系统》,文兰著,高等教育出版社,2015. 2.《微分动力系统原理》,张筑生著,科学出版社,1987,2006. 3.《Differential Equations, Dynamical Systems-An introduction to Chaos》 (Second Edition), Morris W. Hirsch, Stephen Smale, Robert L. Devaney, 2007. 其它(More) 课程大部分内容来自于教材 1 的前三章,教材 2 的前三章,教材 3 的第 15 章。 备注(Notes) 备注说明: 1.带*内容为必填项。 2.课程简介字数为 300-500 字;课程大纲以表述清楚教学安排为宜,字数不限