《初等数论》课程教学大纲 课程基本信息(Course Information) 学时 理程代码 (Course MATH 2402 (Credit 48 学分 Hours) 课程名称 (中文)初等数论 (Course Name) (英文)Elementary Number Theory 课程类型 (Course Type 专业核心选修 授课对家 (Target 本科生 Audience) 授课语言 (Language of全中文 Instruction) “开课院系 数学科学学院 (School) 先修课程 :积分初步,集合论初步,后续课程油象代数代数数论解折数论 (Prerequisite))代数学初步 (nost) “课程负责人 课程网址 (Course (Instructor) Webpage) 本课程是针对数学系二年级本科生开设的专业选修课程,目的是使学生对整数这一数学中 最基本而又无比重要的对象有进一步深入和感件的认识.每个人从小就认识了整数。可是 许我们没有意料到的是 关于整数至今还有很多人类没有能够了解的神秘之处 本课 课程简介(中从古希腊时期的欧几里得所整理的整数的基本理论开始,系统介绍整数的初步理论,包书 文) 整除的基本概念,同余的基本概念,同余式的基本概念,具有重要应用的中国利余定理, (Description)简单不定方程的求解办法,二次互反律和原根等等数论中最基本的基础知识。本课程的教 学目括是通过学习学生在高中阶段或比坡熟的勒学对,加深学生对现代勒学的兴 使学生对上述相关学科产生基本的兴趣,并试图培养进一步研究上述相关领域问的初 能力。初步掌拆数论中一些基本的概念和思维方式。 Elementary Number Theory is for second-year undergraduates in mathematics.The ain of this course is to introduce students the history and the basic theory of numbers. 课程简介(英Everyone knows integers since his childhood times..However,.perhaps most of us do 文) (Description) between integers and theoretical physics!The set of integers with"andis an important class of rings.which have very good algebraic structures.Hence the extensive study of integers will provide students a useful example for his subsequent study on
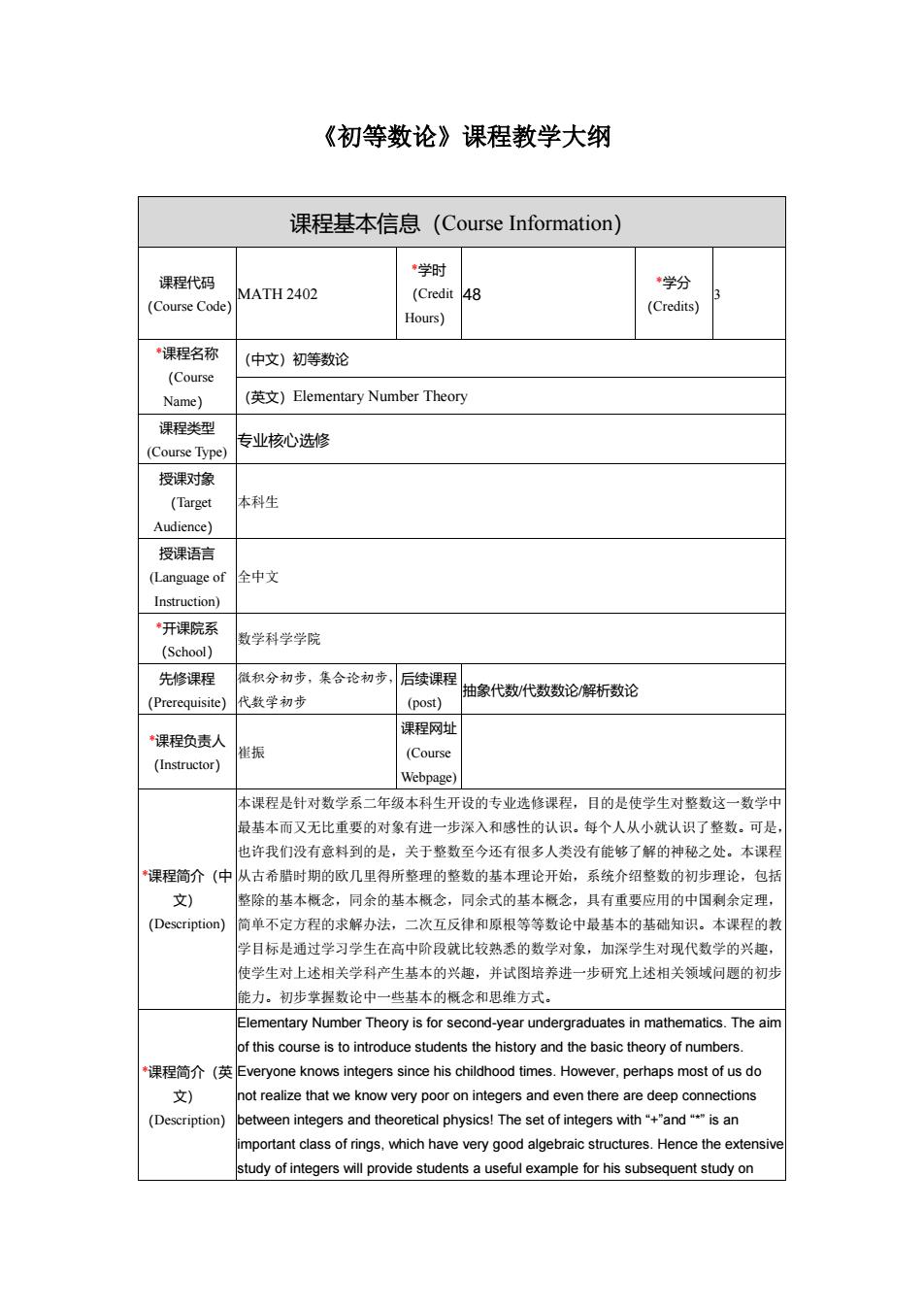
《初等数论》课程教学大纲 课程基本信息(Course Information) 课程代码 (Course Code) MATH 2402 *学时 (Credit Hours) 48 *学分 (Credits) 3 *课程名称 (Course Name) (中文)初等数论 (英文)Elementary Number Theory 课程类型 (Course Type) 专业核心选修 授课对象 (Target Audience) 本科生 授课语言 (Language of Instruction) 全中文 *开课院系 (School) 数学科学学院 先修课程 (Prerequisite) 微积分初步,集合论初步, 代数学初步 后续课程 (post) 抽象代数/代数数论/解析数论 *课程负责人 (Instructor) 崔振 课程网址 (Course Webpage) *课程简介(中 文) (Description) 本课程是针对数学系二年级本科生开设的专业选修课程,目的是使学生对整数这一数学中 最基本而又无比重要的对象有进一步深入和感性的认识。每个人从小就认识了整数。可是, 也许我们没有意料到的是,关于整数至今还有很多人类没有能够了解的神秘之处。本课程 从古希腊时期的欧几里得所整理的整数的基本理论开始,系统介绍整数的初步理论,包括 整除的基本概念,同余的基本概念,同余式的基本概念,具有重要应用的中国剩余定理, 简单不定方程的求解办法,二次互反律和原根等等数论中最基本的基础知识。本课程的教 学目标是通过学习学生在高中阶段就比较熟悉的数学对象,加深学生对现代数学的兴趣, 使学生对上述相关学科产生基本的兴趣,并试图培养进一步研究上述相关领域问题的初步 能力。初步掌握数论中一些基本的概念和思维方式。 *课程简介(英 文) (Description) Elementary Number Theory is for second-year undergraduates in mathematics. The aim of this course is to introduce students the history and the basic theory of numbers. Everyone knows integers since his childhood times. However, perhaps most of us do not realize that we know very poor on integers and even there are deep connections between integers and theoretical physics! The set of integers with “+”and “*” is an important class of rings, which have very good algebraic structures. Hence the extensive study of integers will provide students a useful example for his subsequent study on
mathematics.Number Theory and related topics.The ntegers and divisibility,residues,the modular equations,Chinese Remainder Theorem and applications.first steps to the Diophantine equations.quadratic reciprocity law and the primitive roots and so on. 课程目标与内容(Course objectives and contents) 了解并认识整数的系统知识和基本性质,为将来学习更加抽象的代数对象莫定基础 ◆课程目标(A3.A4.B1.B2.D1) (Course Object))2.体验数论的美感和魅力,提升数学审美能力(A2,B4.C1,C3) 3.通过本课程学习,培养利用所学的数学知识解决简单实际向题的能力A2.A5.B5.C5.D2 章节教学内容(要点) 学时 教学形式 作业及考核课程思政融树应课程目 要求 入点 标 示例: 课程 厂解初等数论的 思考与课后我闲古人与 一些数 课堂讲授 文献搜集查今人对数 2A4,B1 简介 慨。接 问题 的贡献 ◆教学内容讲度 安排及对应课 带金除法转相 数法最大公因数 习愿 程目标(Clas 通过作业使我田古人对 的可小公倍数,算数基本 课堂讲授 A2,B2.C1 Schedule 学生熟练掌数学的贡献 Requirements 除性定理、取整函数和小 握所学内容 数部分 Course Objectives) 课后文献搜 二元一次不定方程 集查阅与习 我国古人 定多元一次不定方程。 A3,A4.C1,G 方程 课堂讲授 通过作业使 今人对数学 3D2 勾股数、费马问题 的贡献 学生热练掌 所学内容 思考与课后进位制及 应用、数 同金的概令、利金类 文健地集花 与剩余系及欧拉函 在实际生 通过作业使中的应用、 阅及习题 A2.A3.B2 数,欧拉定理与费马 课堂讲授 小定理及其应用 学生然练数密码学对 .B5.C5.D1 家安全的 握所学内容 要性
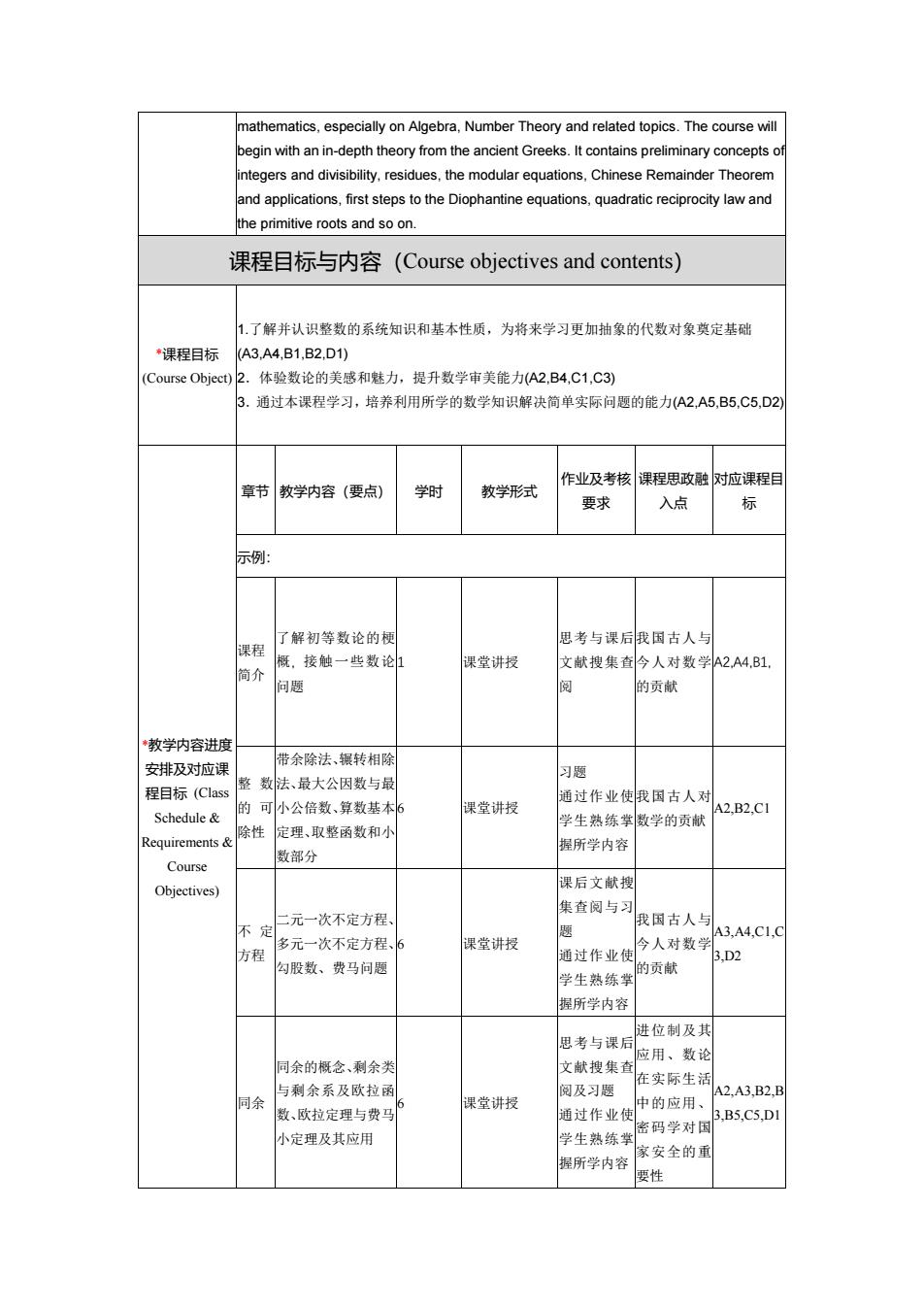
mathematics, especially on Algebra, Number Theory and related topics. The course will begin with an in-depth theory from the ancient Greeks. It contains preliminary concepts of integers and divisibility, residues, the modular equations, Chinese Remainder Theorem and applications, first steps to the Diophantine equations, quadratic reciprocity law and the primitive roots and so on. 课程目标与内容(Course objectives and contents) *课程目标 (Course Object) 1.了解并认识整数的系统知识和基本性质,为将来学习更加抽象的代数对象奠定基础 (A3,A4,B1,B2,D1) 2.体验数论的美感和魅力,提升数学审美能力(A2,B4,C1,C3) 3.通过本课程学习,培养利用所学的数学知识解决简单实际问题的能力(A2,A5,B5,C5,D2) *教学内容进度 安排及对应课 程目标 (Class Schedule & Requirements & Course Objectives) 章节 教学内容(要点) 学时 教学形式 作业及考核 要求 课程思政融 入点 对应课程目 标 示例: 课程 简介 了解初等数论的梗 概, 接触一些数论 问题 1 课堂讲授 思考与课后 文献搜集查 阅 我国古人与 今人对数学 的贡献 A2,A4,B1, 整 数 的 可 除性 带余除法、辗转相除 法、最大公因数与最 小公倍数、算数基本 定理、取整函数和小 数部分 6 课堂讲授 习题 通过作业使 学生熟练掌 握所学内容 我国古人对 数学的贡献 A2,B2,C1 不 定 方程 二元一次不定方程、 多元一次不定方程、 勾股数、费马问题 6 课堂讲授 课后文献搜 集查阅与习 题 通过作业使 学生熟练掌 握所学内容 我国古人与 今人对数学 的贡献 A3,A4,C1,C 3,D2 同余 同余的概念、剩余类 与剩余系及欧拉函 数、欧拉定理与费马 小定理及其应用 6 课堂讲授 思考与课后 文献搜集查 阅及习题 通过作业使 学生熟练掌 握所学内容 进位制及其 应用、数论 在实际生活 中的应用、 密码学对国 家安全的重 要性 A2,A3,B2,B 3,B5,C5,D1
思考与课后 司会方程的基太 会含、孙子定理、高沙 我古人 课堂讲授 阅及习避 A3.A4.CI.C 今人对数 方程同余方程,素数模 通过作业色 .D2 的贡献 同余方程 学生熟练 据所学内容 次二次同余方程 思考与后 文献搜集 勒让德符号与雅可 我国古人 方程 阅及习题 A2.A3.B2.E 比符号、素数表为二: 课堂讲授 今人对数 与平 通过作业付 3.B5.C5.D3 整数平方和、拉格额 的贡献 方 学生熟练生 日四平方定理 所学内容 思考与课局 指数及其基本性质 文献搜集百 原 我用古人号 原根存在定理、二项 闷及习题 A2A4B2 与指同余方程的求解、商 课堂讲授 今人对数 用过作业使 次剩余的基 学生搭练的页献 握所学内容 思考与课后 文献搜集查 我古人 课堂讲授 阅及习题 通过作业 今人对数 2A4B2 数分分布探究 的贡献 ,C3,D1 学生掌握所 布 学内容 思考与课后 代数上次代数数高次 文献集查 国古人 数与数数、超越数的松 超越造、e与pi的超越 课堂讲授 阅及习题 4.B1B2.E 今人对数 通过作业件 4.C1 数 性 的贡献 学生掌操用 学内容 思考与课后 文献搜集查 连分连分数的基本概念 我国吉人 A2.A4.BI.E 阅及习翼 数与性质,表实数为连! 课堂讲授 今人对数学.B4,C1,C3 通过作业使 分数、循环连分贸 学生握所 的贡献 3D3 学内容 注1:建议按照教学周周学时综排. 注2:相应章节的课程思政融入点根据实际情况填写。 考核方式 平时作业及课堂参与度20分 (Grading) (2)期末考试80分
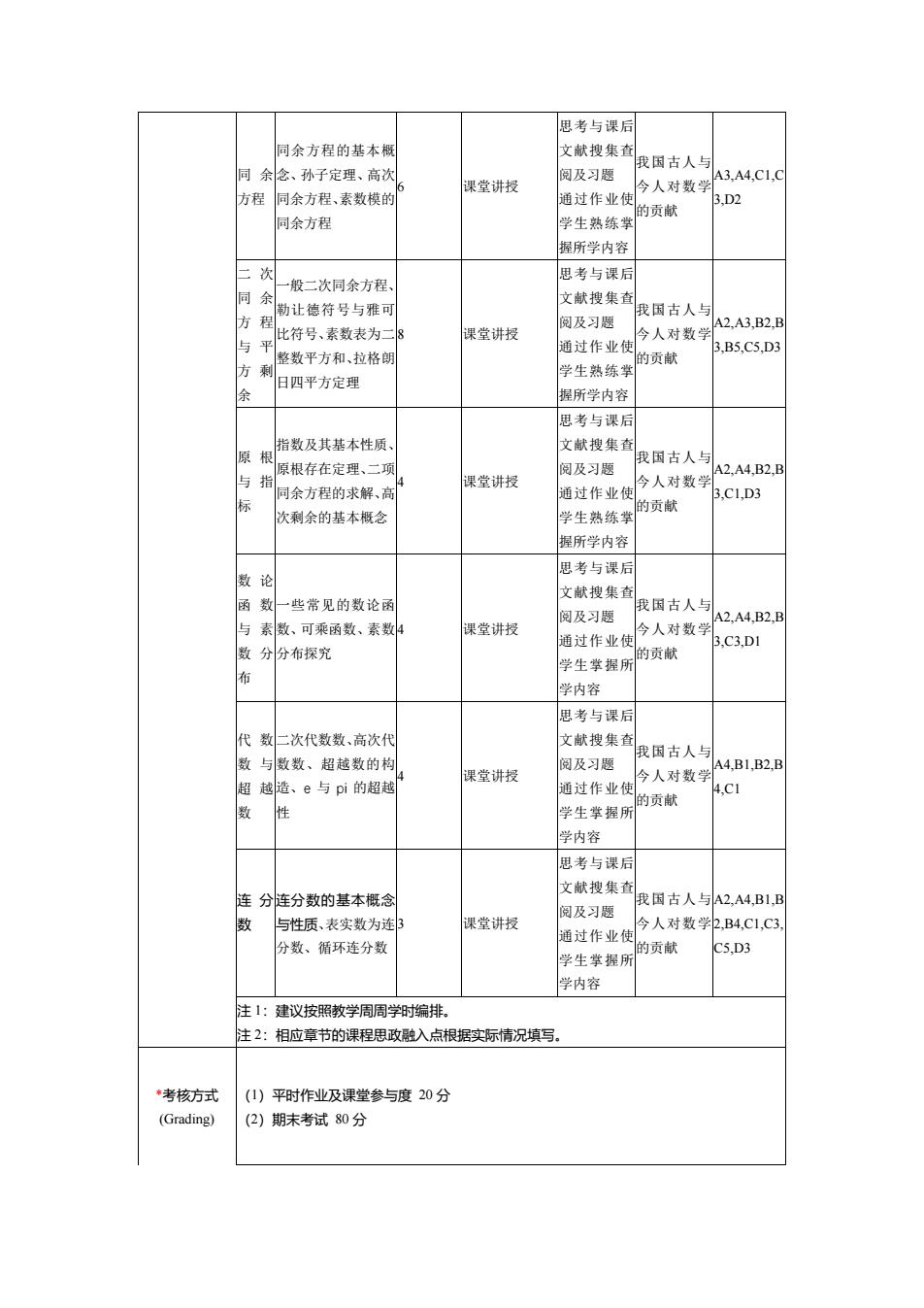
同 余 方程 同余方程的基本概 念、孙子定理、高次 同余方程、素数模的 同余方程 6 课堂讲授 思考与课后 文献搜集查 阅及习题 通过作业使 学生熟练掌 握所学内容 我国古人与 今人对数学 的贡献 A3,A4,C1,C 3,D2 二 次 同 余 方 程 与 平 方 剩 余 一般二次同余方程、 勒让德符号与雅可 比符号、素数表为二 整数平方和、拉格朗 日四平方定理 8 课堂讲授 思考与课后 文献搜集查 阅及习题 通过作业使 学生熟练掌 握所学内容 我国古人与 今人对数学 的贡献 A2,A3,B2,B 3,B5,C5,D3 原 根 与 指 标 指数及其基本性质、 原根存在定理、二项 同余方程的求解、高 次剩余的基本概念 4 课堂讲授 思考与课后 文献搜集查 阅及习题 通过作业使 学生熟练掌 握所学内容 我国古人与 今人对数学 的贡献 A2,A4,B2,B 3,C1,D3 数 论 函 数 与 素 数 分 布 一些常见的数论函 数、可乘函数、素数 分布探究 4 课堂讲授 思考与课后 文献搜集查 阅及习题 通过作业使 学生掌握所 学内容 我国古人与 今人对数学 的贡献 A2,A4,B2,B 3,C3,D1 代 数 数 与 超 越 数 二次代数数、高次代 数数、超越数的构 造、e 与 pi 的超越 性 4 课堂讲授 思考与课后 文献搜集查 阅及习题 通过作业使 学生掌握所 学内容 我国古人与 今人对数学 的贡献 A4,B1,B2,B 4,C1 连 分 数 连分数的基本概念 与性质、表实数为连 分数、循环连分数 3 课堂讲授 思考与课后 文献搜集查 阅及习题 通过作业使 学生掌握所 学内容 我国古人与 今人对数学 的贡献 A2,A4,B1,B 2,B4,C1,C3, C5,D3 注 1:建议按照教学周周学时编排。 注 2:相应章节的课程思政融入点根据实际情况填写。 *考核方式 (Grading) (1)平时作业及课堂参与度 20 分 (2)期末考试 80 分

教材 教材或参考资 等数论,闵嗣、严士能,高等教有出版社,2020,第四版,15BN978-704-5346- 参考书目: &Other Materials) 初等数论,潘承洞.潘承彪著,北京大学出版社,2013,书号978-7-301-21612-5 哈代数论,(英)G.H.Hardy,E.M.Wright著,人民邮电出版社,2009,书号9787115214270 其它(More) 备注Notes) 备注说明: 1.带内容为必填项。 2.课程简介字数为300-500字;课程大纲以表述清楚教学安排为宜,字数不限】
*教材或参考资 料 (Textbooks & Other Materials) 教材: 初等数论, 闵嗣鹤、严士健, 高等教育出版社, 2020, 第四版, ISBN 978-7-04-53446-7 参考书目: 初等数论,潘承洞, 潘承彪著,北京大学出版社,2013,书号:978-7-301-21612-5 哈代数论,(英)G. H. Hardy,E. M. Wright 著,人民邮电出版社,2009,书号:9787115214270 其它(More) 备注(Notes) 备注说明: 1.带*内容为必填项。 2.课程简介字数为 300-500 字;课程大纲以表述清楚教学安排为宜,字数不限