《实分析与傅里叶分析》课程教学大纲 课程基本信息(Course Information) 学时 课程代码 MATH2650 (Credit 学分 (Course Cod Hours) (Credits) *课程名称 (中文)实分析与傅里叶分析 (Course Name) (英文)Real analysisand Fourier analysis 课程类型 专业必修 (Course Type) 授课对橡 (Target 本科生 Audience) 授课语言 (Language of双语 Instruction) “开课院系 数学科学学院、致远学院 (School) 先修课程 后续课程 数学分析 (Prerequisite) (Dost) 泛函分析 *课程负责人 课程网 来米加 http://math.sjtu.edu.cn/faculty/mlai/teaching/teachin (Course (Instructor) Webpage) g.html (中文300-500字,含课程性质。主要教学内容、课程教学目标等) “课程简介(中本课程主要介绍勒贝格积分理论以及傅里叶分析。第一部分主要内容是勒贝格测度、勒贝 格积分、微分理论。第二部分介绍傅里叶级数,傅里叶变换初步及其应用。本课程为后续 (Description) 分方程、调和分析、泛函分析等课程提供理论基础 (英文300-500字) This course mainly introduces two aspects:Lebesgue integral theory and Fourier analysis.The first part covers Lebesgue measure,integration and differentiation theory.The second part 课程简介(英discusses Fourier series,Fourier transform,,Hilbert space and some applications.This course vides sub t courses suc nalysis and functional analysis
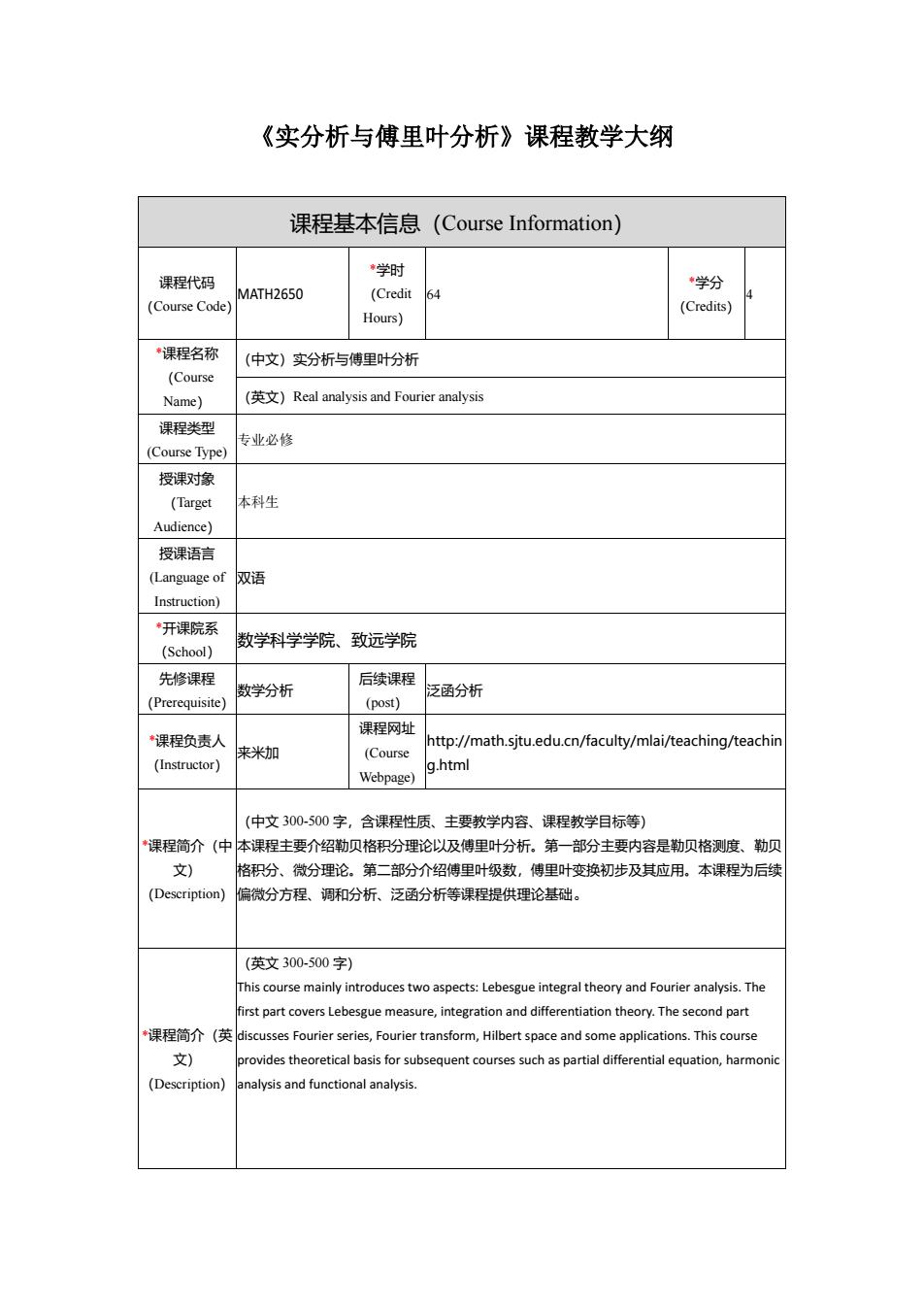
《实分析与傅里叶分析》课程教学大纲 课程基本信息(Course Information) 课程代码 (Course Code) MATH2650 *学时 (Credit Hours) 64 *学分 (Credits) 4 *课程名称 (Course Name) (中文)实分析与傅里叶分析 (英文)Real analysis and Fourier analysis 课程类型 (Course Type) 专业必修 授课对象 (Target Audience) 本科生 授课语言 (Language of Instruction) 双语 *开课院系 (School) 数学科学学院、致远学院 先修课程 (Prerequisite) 数学分析 后续课程 (post) 泛函分析 *课程负责人 (Instructor) 来米加 课程网址 (Course Webpage) http://math.sjtu.edu.cn/faculty/mlai/teaching/teachin g.html *课程简介(中 文) (Description) (中文 300-500 字,含课程性质、主要教学内容、课程教学目标等) 本课程主要介绍勒贝格积分理论以及傅里叶分析。第一部分主要内容是勒贝格测度、勒贝 格积分、微分理论。第二部分介绍傅里叶级数,傅里叶变换初步及其应用。本课程为后续 偏微分方程、调和分析、泛函分析等课程提供理论基础。 *课程简介(英 文) (Description) (英文 300-500 字) This course mainly introduces two aspects: Lebesgue integral theory and Fourier analysis. The first part covers Lebesgue measure, integration and differentiation theory. The second part discusses Fourier series, Fourier transform, Hilbert space and some applications. This course provides theoretical basis for subsequent courses such as partial differential equation, harmonic analysis and functional analysis

课程目标与内容(Course objectives and contents) 掌并熟练运用勒贝格测度和积分。(A4,B1,B2,C3,C5,D1 课程目标 ,深入理解勒贝格微分理论。 (A4,B1,B2,C3,C5,D1) (Course Object) 3.掌握博里叶级数,傅里叶变换,希尔伯特空间的基础知识。(A4,B1,B2,C3,C5,D1 4.了解博里叶级数和变换的一些应用。(A4,B1,B2,C3,C5,D1) 教学内容 课程思改融 对应 章节 学时教学形式 作业及考核要求 (要点) 入点 课程 目标 示例 通过课程得 到思维训 练,了解人 集合,欧式 掌握本课程集合论以及点集类理性文明 课堂授课拓扑的相关术语和他们的基的精彩华 B2,C3 空间点集拓6 扑 本含义 卓,捉高数 C5.D 学索养,培 教学内空 通过课程得 安排及对应味 到思维训 程目标(Clas Schedule& 掌挥外测度的定义,可测 练了解人 B1 课堂授课 的Caratheodory判据 不类理性文明2C 可测集的存在性,以及一个 的精彩华 章,提高数 S.D Objectives 可测集的结构 学索养,培 养刻苦专研 精神 通过课程得 到思维训 4 练,了解人 B1 掌握可测函数的定义,及其能理性文明 课堂授 连续函数的关系, 的精彩华 ewood三原则 章,提高数 5,D 学素养,培, 养刻苦专研 精神 Lebesgue积分的框架,通过课程得A4 勒贝格积分10 课堂授课 以及积分和极限交换的三大到思维训B1 定理:单调收敛定理、Fatou练,了解人B2,C3
课程目标与内容(Course objectives and contents) *课程目标 (Course Object) 1.掌握并熟练运用勒贝格测度和积分。(A4, B1,B2,C3, C5,D1) 2.深入理解勒贝格微分理论。(A4, B1,B2,C3, C5,D1) 3.掌握傅里叶级数,傅里叶变换,希尔伯特空间的基础知识。(A4, B1,B2,C3, C5,D1) 4.了解傅里叶级数和变换的一些应用。(A4, B1,B2,C3, C5,D1) *教学内容进度 安排及对应课 程目标 (Class Schedule & Requirements & Course Objectives) 章节 教学内容 (要点) 学时 教学形式 作业及考核要求 课程思政融 入点 对应 课程 目标 示例: 1 集合,欧式 空间点集拓 扑 6 课堂授课 掌握本课程集合论以及点集 拓扑的相关术语和他们的基 本含义 通过课程得 到思维训 练,了解人 类理性文明 的精彩华 章,提高数 学素养,培 养刻苦专研 精神 A4, B1, B2,C3 , C5,D 1 2 测度 6 课堂授课 掌握外测度的定义,可测集 的 Caratheodory 判据,不 可测集的存在性,以及一个 可测集的结构 通过课程得 到思维训 练,了解人 类理性文明 的精彩华 章,提高数 学素养,培 养刻苦专研 精神 A4, B1 , B2,C3 , C5,D 1 3 可测函数 4 课堂授课 掌握可测函数的定义,及其 和 连 续 函 数 的 关 系 , Littlewood 三原则 通过课程得 到思维训 练,了解人 类理性文明 的精彩华 章,提高数 学素养,培 养刻苦专研 精神 A4, B1 , B2,C3 , C5,D 1 4 勒贝格积分 10 课堂授课 掌握 Lebesgue 积分的框架, 以及积分和极限交换的三大 定理:单调收敛定理、Fatou 通过课程得 到思维训 练,了解人 A4, B1 , B2,C3
引理、控制收敛定理。了解类理性文明 Lebe5gue积分和翠曼积分的精彩华C5D 惊,提高数 学素养,培 养刻苦专研 神 通过课程得 到思维 A4 掌握Lebesgue关于单调函练,了解人 B1 数几乎处处可微的定理,了楼理性文明 微分理论 课堂授课 解在Lebesgue积分框架下的精彩华 的Ne ton-Leibniz公式 提高数 立的充要条件:绝对连续 学素养,培 s,D 养刻苦专研 鞋神 通过课程得 解一检拓扑空间上的测皮思维训A4 和积哈,初步理解Rez表,了解人1 抽象测度积6 类理性文明 示定理也就是将关于测度 B2.C3 课堂授评 的积分看做为正线性泛函的 的精彩华 分理论 对偶观点 ,提高数 S.D 学素养,培 养刻苦专研 结神 通过课程得 了解周期为2π的函数的健 博里叶级数B 课堂授课 里叶级敌,及其相应的收敛 结果 的精彩华B2,C3 章,提高数 学索养, 刻苦专研 精神 通过课程得 到思维训 练,了解 学上速降函数空间上的理性文明 .C 傅里叶变换8 课堂授课傅里叶变换,逆变换,反演的精彩华 公式等 摩,提高数 5.D 学养,培 侨刻苦专研 精神 博甲叶分析 课堂授课 初步了解Fourier分析的一通过课程得A4, 应用实例 些应用:如在概率、数论、到思维训B1
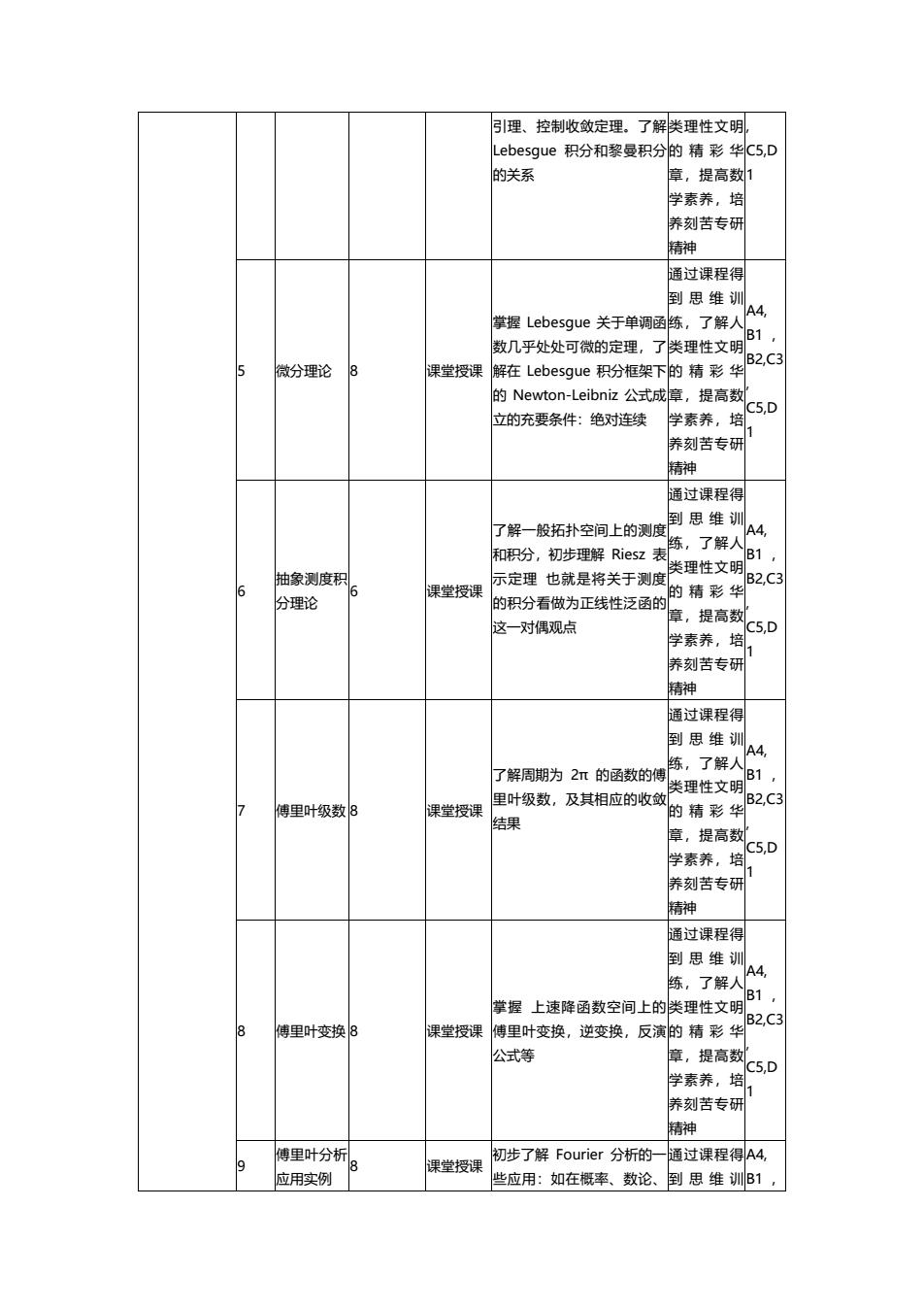
引理、控制收敛定理。了 解 Lebesgue 积分和黎曼积分 的关系 类理性文明 的精彩华 章,提高数 学素养,培 养刻苦专研 精神 , C5,D 1 5 微分理论 8 课堂授课 掌握 Lebesgue 关于单调函 数几乎处处可微的定理,了 解在 Lebesgue 积分框架下 的 Newton-Leibniz 公式成 立的充要条件:绝对连续 通过课程得 到思维训 练,了解人 类理性文明 的精彩华 章,提高数 学素养,培 养刻苦专研 精神 A4, B1 , B2,C3 , C5,D 1 6 抽象测度积 分理论 6 课堂授课 了解一般拓扑空间上的测度 和积分,初步理解 Riesz 表 示定理 也就是将关于测度 的积分看做为正线性泛函的 这一对偶观点 通过课程得 到思维训 练,了解人 类理性文明 的精彩华 章,提高数 学素养,培 养刻苦专研 精神 A4, B1 , B2,C3 , C5,D 1 7 傅里叶级数 8 课堂授课 了解周期为 2 π 的函数的傅 里叶级数,及其相应的收敛 结果 通过课程得 到思维训 练,了解人 类理性文明 的精彩华 章,提高数 学素养,培 养刻苦专研 精神 A4, B1 , B2,C3 , C5,D 1 8 傅里叶变换 8 课堂授课 掌握 上速降函数空间上的 傅里叶变换,逆变换,反演 公式等 通过课程得 到思维训 练,了解人 类理性文明 的精彩华 章,提高数 学素养,培 养刻苦专研 精神 A4, B1 , B2,C3 , C5,D 1 9 傅里叶分析 应用实例 8 课堂授课 初步了解 Fourier 分析的一 些应用:如在概率、数论、 通过课程得 到思维训 A4, B1

离散几何中的应用 练,了解人B2C3 章,提高数 学素养,培 养刻苦专研 精神 注1:建议按照教学周周学时编排。 注2:相应章节的课程思政融入点根据实际情况填写! 30%作业+20%小则+50%期末考试 该课程的平时成绩主要根据作业情况给出,占比30%。为了鼓励学有余力,或者想对课程 考核方式 内容做更进一步拓展的学生,平时作业有些选做题,阅读题。这部分内容允许学生学判 (Grading) 结束前统一提交,将视完成情况给与附加分。此外为了确保大多数学生跟随进度,同时也 为更好了解学生草操情况,在期中安排一次小测,占比20%。课程结束安排期末考试,占 比50%,以统一命题的形式。 敦材或参考资 1.自编讲义详见课程主页 料(Textbook 2.《实分析》Elias M.Stein,Rami Shakarchit世界图书出版公司 Other 3.《傅里叶分析》Elias M.Stein,Rami Shakarchi世界图书出版公司 Materials) 其它(More) 备注(Notes) 备注说明: 1.带内容为必填项。 2.课程简介字数为300500字:课程大纲以表述清楚牧学安排为宜,字数不限
离散几何中的应用 练,了解人 类理性文明 的精彩华 章,提高数 学素养,培 养刻苦专研 精神 B2,C3 , C5,D 1 注 1:建议按照教学周周学时编排。 注 2:相应章节的课程思政融入点根据实际情况填写。 *考核方式 (Grading) 30%作业+20%小测+50%期末考试 该课程的平时成绩主要根据作业情况给出,占比 30%。为了鼓励学有余力,或者想对课程 内容做更进一步拓展的学生,平时作业有一些选做题,阅读题。这部分内容允许学生学期 结束前统一提交,将视完成情况给与附加分。此外为了确保大多数学生跟随进度,同时也 为更好了解学生掌握情况,在期中安排一次小测,占比 20%。课程结束安排期末考试,占 比 50%,以统一命题的形式。 *教材或参考资 料 (Textbooks & Other Materials) 1. 自编讲义 详见课程主页 2.《实分析》Elias M.Stein, Rami Shakarchi 世界图书出版公司 3.《傅里叶分析》Elias M.Stein, Rami Shakarchi 世界图书出版公司 其它(More) 备注(Notes) 备注说明: 1.带*内容为必填项。 2.课程简介字数为 300-500 字;课程大纲以表述清楚教学安排为宜,字数不限