
《高等代数(荣誉)》课程教学大纲 课程基本信息(Course Information) 的 课程代码 MATH 1405H 学纷 (Course Code (Credis)s Hour s) ·课程名称 (中文)高等代数(荣誉)1 (Course Name) (英文)Advanced Algebra(H)I 课程类型 基础必修课 (Course Type) 授课对象 (Target 本科生 Audience) 授课语言 (Language of双语 Instruction) 开课院系 数学科学学院 (School) 后续树 先修课程 课 (Prerequ site) 高等代数山 课程 网址 (Cou “课程负责人 张跃辉 (Instructor) page 高等代数是数学专业本科教学的最重要的基础课程之 其其木内突为多 式、线性方程组、线性空间、线性映射、线性算子谱理论、多重线性代数、若 课程简介(中 当标准型理论等等,具有高度的抽象性与广泛的应用性,是人类思维高度发展 的象征。高等代数是代数学的重要内容。我国古代数学发展的主线都与代数学, 文) 尤其是高等代数学密切相关,以中国剩余定理为光辉代表。当代信息社会中 (Description) 计算机、网络、通信、信息安全、视频图像处理中很多基础理论源于高等代数 本课程的目标是使学生通过课程的学习,对线性代数产生根本的兴趣,为进 步学习高等代数抽象理论建立良好基础
《高等代数(荣誉)I》课程教学大纲 课程基本信息(Course Information) 课程代码 (Course Code) MATH 1405H *学 时 (Cr edit Hour s) 80 *学分 (Credits) 5 *课程名称 (Course Name) (中文)高等代数(荣誉)I (英文)Advanced Algebra(H) I 课程类型 (Course Type) 基础必修课 授课对象 (Target Audience) 本科生 授课语言 (Language of Instruction) 双语 *开课院系 (School) 数学科学学院 先修课程 (Prerequisite) 无 后续 课程 (post ) 高等代数 II *课程负责人 (Instructor) 张跃辉 课程 网址 (Cou rse Web page ) *课程简介(中 文) (Description) 高等代数是数学专业本科教学的最重要的基础课程之一,其基本内容为多项 式、线性方程组、线性空间、线性映射、线性算子谱理论、多重线性代数、若 当标准型理论等等,具有高度的抽象性与广泛的应用性,是人类思维高度发展 的象征。高等代数是代数学的重要内容。我国古代数学发展的主线都与代数学, 尤其是高等代数学密切相关,以中国剩余定理为光辉代表。当代信息社会中, 计算机、网络、通信、信息安全、视频图像处理中很多基础理论源于高等代数。 本课程的目标是使学生通过课程的学习,对线性代数产生根本的兴趣,为进一 步学习高等代数抽象理论建立良好基础
(英文30-500字) Linear algebra is one of the fundamental courses in physics.It also plays an important role in physics,engineering and computer sciences.Its main *课程简介(英contents include linear equations,,linear space,linear mapping,linear operato spectrum theory,multilinear algebra,Jordan standard theory polynomial,etc (Description) The main goal of this course is to enable students to havea solid base of understanding in linear algebra.Geometric viewpoints will be emphasized throughout the course. 课程目标与内容(Course objectives and contents) 能理解高等代数的基本理论,提高抽象思维能力。(B1) 课程目标2.能运用高等代数的基本方法,解决一些基本的线性问题。(B2) (Course Object))能引导学生培养自我学习能力,并养成终身学习的习惯.(C5) !引导学牛形成批判性思维,并将高等代数运用干实践,加以创新,解决新的问题。(C3 里理甲攻时应理 教学内容(要点)教学目标学时 教学形式作业及考核要求 融入点程目标 课程导引 直观理解 理论课与 11:8-26 统思维 知识扬 习题课 教学内容进 12.17.20 安排及对应 13:3.6-13 程目标(C1as Schedule& 量与矩阵简 理论课 2.1:5-8 17-2 2.2:11,18,20 知识探 Requirements 介,线性方程组院全掌握 5 习题课 学科知识 2.3:12379,1 究 Course 周与矩阵代数 17. Objectives) 18 19,22,23,25-28 2.4:7,9,15, 第饯性方程组与 理论课 21-24:32-34 三矩阵代数:线性完全掌据 5 习题课 2.5:3,7,9,21,辩证法 价值 周空间 23,29.30,32
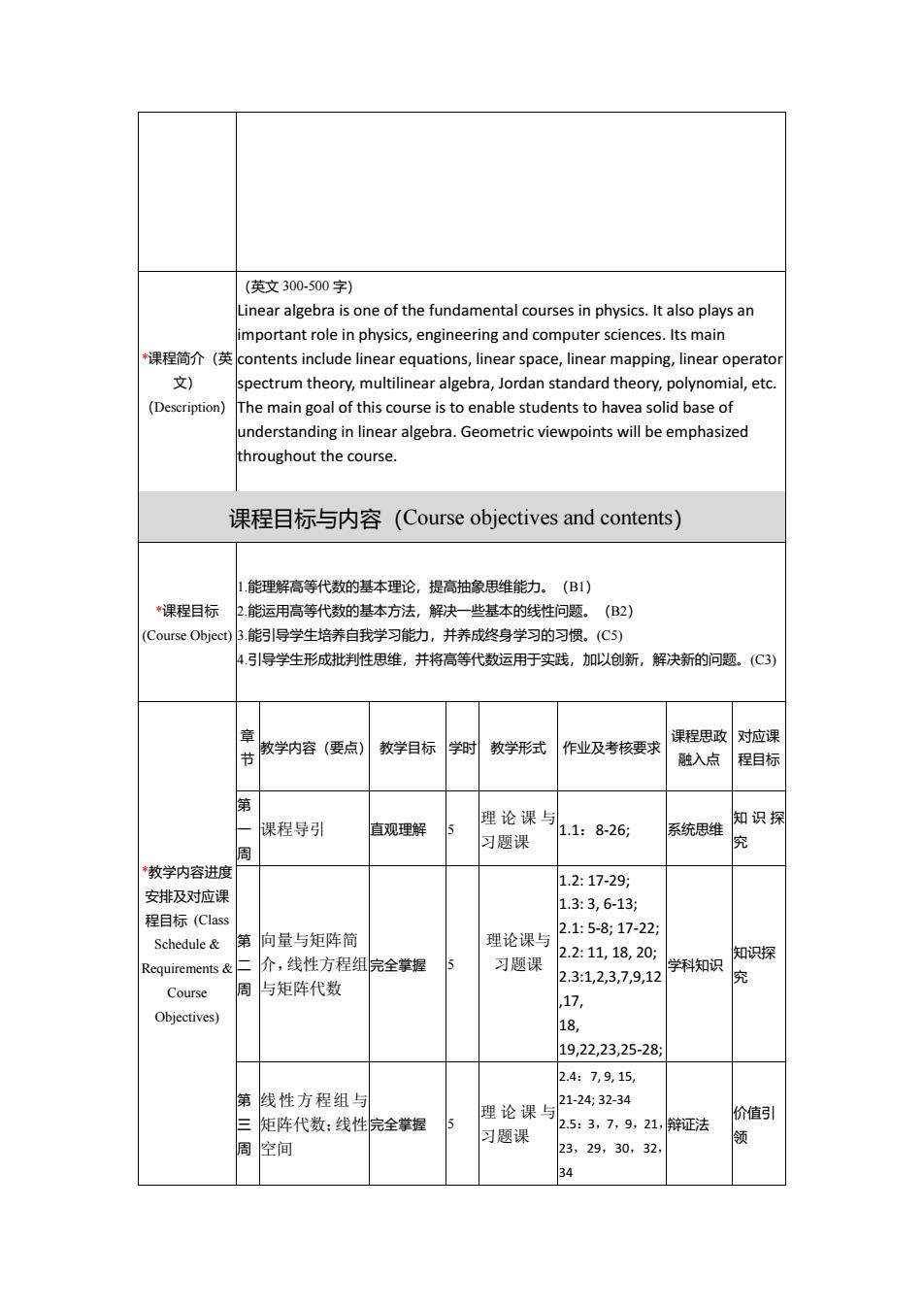
*课程简介(英 文) (Description) (英文 300-500 字) Linear algebra is one of the fundamental courses in physics. It also plays an important role in physics, engineering and computer sciences. Its main contents include linear equations, linear space, linear mapping, linear operator spectrum theory, multilinear algebra, Jordan standard theory, polynomial, etc. The main goal of this course is to enable students to havea solid base of understanding in linear algebra. Geometric viewpoints will be emphasized throughout the course. 课程目标与内容(Course objectives and contents) *课程目标 (Course Object) 1.能理解高等代数的基本理论,提高抽象思维能力。(B1) 2.能运用高等代数的基本方法,解决一些基本的线性问题。(B2) 3.能引导学生培养自我学习能力,并养成终身学习的习惯。(C5) 4.引导学生形成批判性思维,并将高等代数运用于实践,加以创新,解决新的问题。(C3) *教学内容进度 安排及对应课 程目标 (Class Schedule & Requirements & Course Objectives) 章 节 教学内容(要点) 教学目标 学时 教学形式 作业及考核要求 课程思政 融入点 对应课 程目标 第 一 周 课程导引 直观理解 5 理论课与 习题课 1.1:8-26; 系统思维 知识探 究 第 二 周 向量与矩阵简 介,线性方程组 与矩阵代数 完全掌握 5 理论课与 习题课 1.2: 17-29; 1.3: 3, 6-13; 2.1: 5-8; 17-22; 2.2: 11, 18, 20; 2.3:1,2,3,7,9,12 ,17, 18, 19,22,23,25-28; 学科知识 知识探 究 第 三 周 线性方程组与 矩阵代数;线性 空间 完全掌握 5 理论课与 习题课 2.4:7, 9, 15, 21-24; 32-34 2.5:3,7,9,21, 23,29,30,32, 34 辩证法 价值引 领
2.6:5,7,13,16 19.27:4.5 7,9,11-15,17 18,19.24,32 34,35 线性空间、子空 第向、四个子 2A1,59,10,12 子空间计算 理论课与14 四间、直和分解 认识论和价值 与直和份解 习题课 283.457.8 方法论领 周【需两本教材同 时使用) 线性空间、子空 第间、四个子 臣间、直和分解子空间计算 理论课与2B3,4,5,7,8 格养 与直和分解 周【需两本教材同 习题课 创新思维成 时使用 线性空间、子空 间、四个子 间、直和分解子空间计篇 理论课与 2C1,3,8,9,10: 学科知识 知识探 【需两本教材同与直和分轻 习题课 究 时使用: 线性空间、子空 间、四个子空 间、直和分解 需两本教材同 时使用):投 仔空间计等 与直和分 七与正交化方法 理论课与2C:12,14,15,16,职业道德能力建 解,理解最 周(仅限讨论欧 习题课17; 建设设 小二乘法 氏空间Rn中的 抽象内积空间 投影与正交化 方法(仅眼讨设 4.1:3.4.7.10 第 欧氏空间R叫 理解最小5 理论课与13,16,23-26 学科知识 知识 周 的投影,暂不涉乘法 习题课 4.2:13,17 究 及抽象内积空 19,23: 间) 行列式初步(可 51 第 用交错多重线 1-5,78,1113,1 性函数定义,由 理论课与5, 九 计算行列式5 17,18,爱国情怀能力建 此导出其它定 习题课 27,28,29,30: 引领设 义,淡化计算技 5.2: 4,7.9,10,12,15
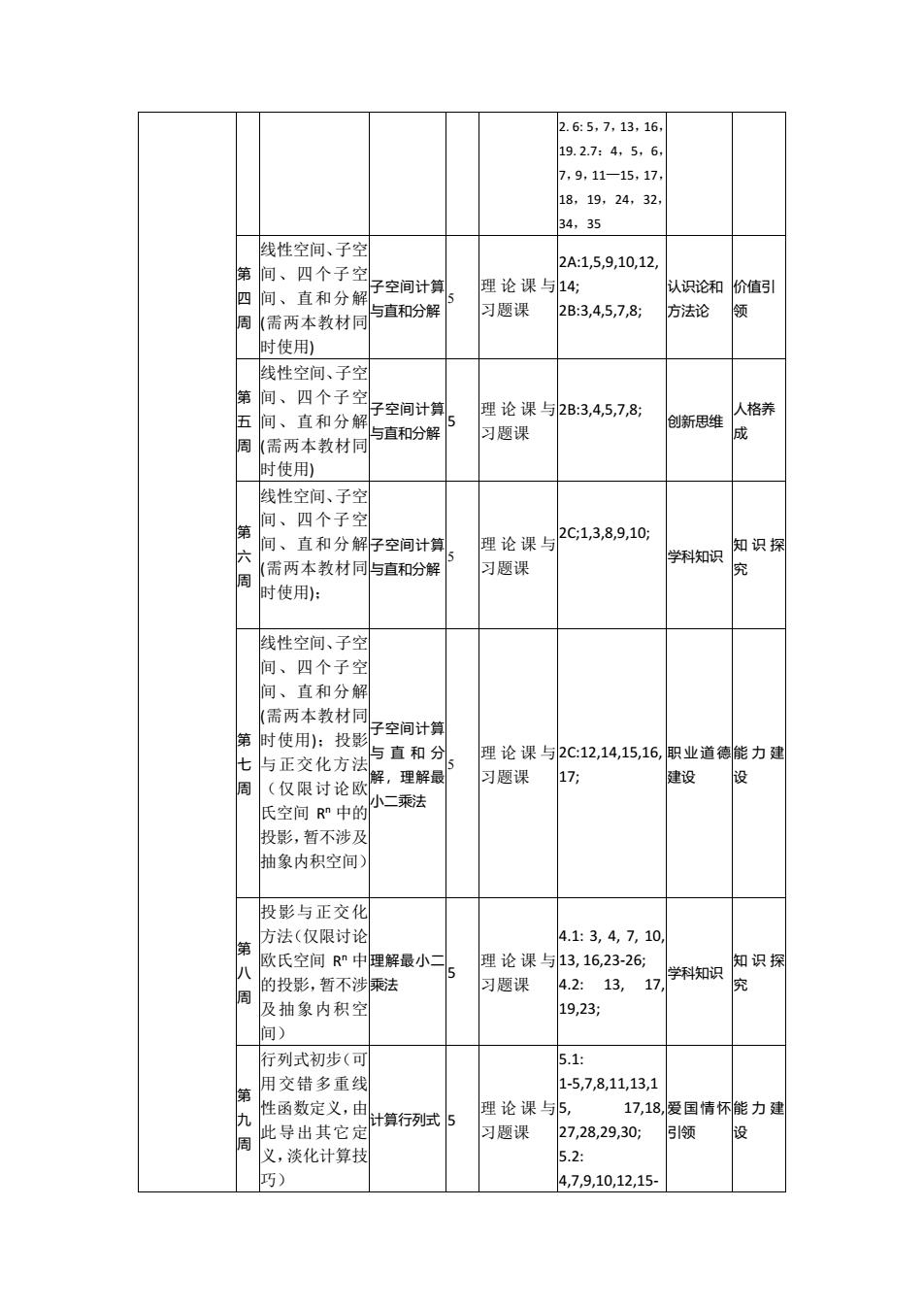
2. 6: 5,7,13,16, 19. 2.7:4,5,6, 7,9,11—15,17, 18,19,24,32, 34,35 第 四 周 线性空间、子空 间、四个子空 间、直和分解 (需两本教材同 时使用) 子空间计算 与直和分解 5 理论课与 习题课 2A:1,5,9,10,12, 14; 2B:3,4,5,7,8; 认识论和 方法论 价值引 领 第 五 周 线性空间、子空 间、四个子空 间、直和分解 (需两本教材同 时使用) 子空间计算 与直和分解 5 理论课与 习题课 2B:3,4,5,7,8; 创新思维 人格养 成 第 六 周 线性空间、子空 间、四个子空 间、直和分解 (需两本教材同 时使用); 子空间计算 与直和分解 5 理论课与 习题课 2C;1,3,8,9,10; 学科知识 知识探 究 第 七 周 线性空间、子空 间、四个子空 间、直和分解 (需两本教材同 时使用);投影 与正交化方法 (仅限讨论欧 氏空间 R n 中的 投影,暂不涉及 抽象内积空间) 子空间计算 与直和分 解,理解最 小二乘法 5 理论课与 习题课 2C:12,14,15,16, 17; 职业道德 建设 能力建 设 第 八 周 投影与正交化 方法(仅限讨论 欧氏空间 R n 中 的投影,暂不涉 及抽象内积空 间) 理解最小二 乘法 5 理论课与 习题课 4.1: 3, 4, 7, 10, 13, 16,23-26; 4.2: 13, 17, 19,23; 学科知识 知识探 究 第 九 周 行列式初步(可 用交错多重线 性函数定义,由 此导出其它定 义,淡化计算技 巧) 计算行列式 5 理论课与 习题课 5.1: 1-5,7,8,11,13,1 5, 17,18, 27,28,29,30; 5.2: 4,7,9,10,12,15- 爱国情怀 引领 能力建 设
19.23.25.265.3 1,4-7,9,10,14,2 0.25-29,34 特征值与特征 向量,对角化, 次型 Jordan谱理论 对 第标准型(需两本角化、实对 理论课 6.12,455,89 十数材同时使用,称矩阵,二5 1113.16,19.20 艺术文化人格养 周Jordan标准型次型.Jordan 习题课 培养 成 21,25,2728: 可用归纳法,入标准型 矩阵、循环 间等交习题课) 特征值与特征 向量,对角化, 6.2:13.489.1 二次型,lordan理论、 12, 第十 标准型(需两本角化 实 15,16,23,26,30 教材同时使用,称矩阵 理论课与31,32: 文化责任知识探 Jordan标准型次型、orda 习题课 6.4: 23,78 究 10.12. 可用归纳法,标准型 16,17,18,20,23 矩阵、循环子空 间等交习题课 4,25 特征值与特征 向量,对角化 二次型,Jordan谱理论、对 6.5:4.5.6.8.9.10 标准型(需两本角化、实刘 121516182 教材同时使用 称矩阵、 理论课 24,26,31 Jordan标准型次型.Jordan5 7.1:1-4,7:7.2:4, 科学精神 知识探 习题课 究 可用归纳法,入标准型: 6.10. 矩阵、循环子空计算sVD 11.13.16.18.19 间等交习题谱分解 23-27: 课): 5vD分解 SvD分解: 第线性变换初步、针算SVD 7.4:4.7.1113.1 理论里 定理(本章需两理解线性( 习题课 6,17,19-22 元发展 能力 设 周本教材同时使数基本定理 3.A3,4,7-14 用 线性弯换初步 第十 饯性代数基 理解线性代 理论课 B:4-12.17,20.2 定理(本章需 道德教育 能力建 数基本定理 习题课30 设 本教材同时使 用)
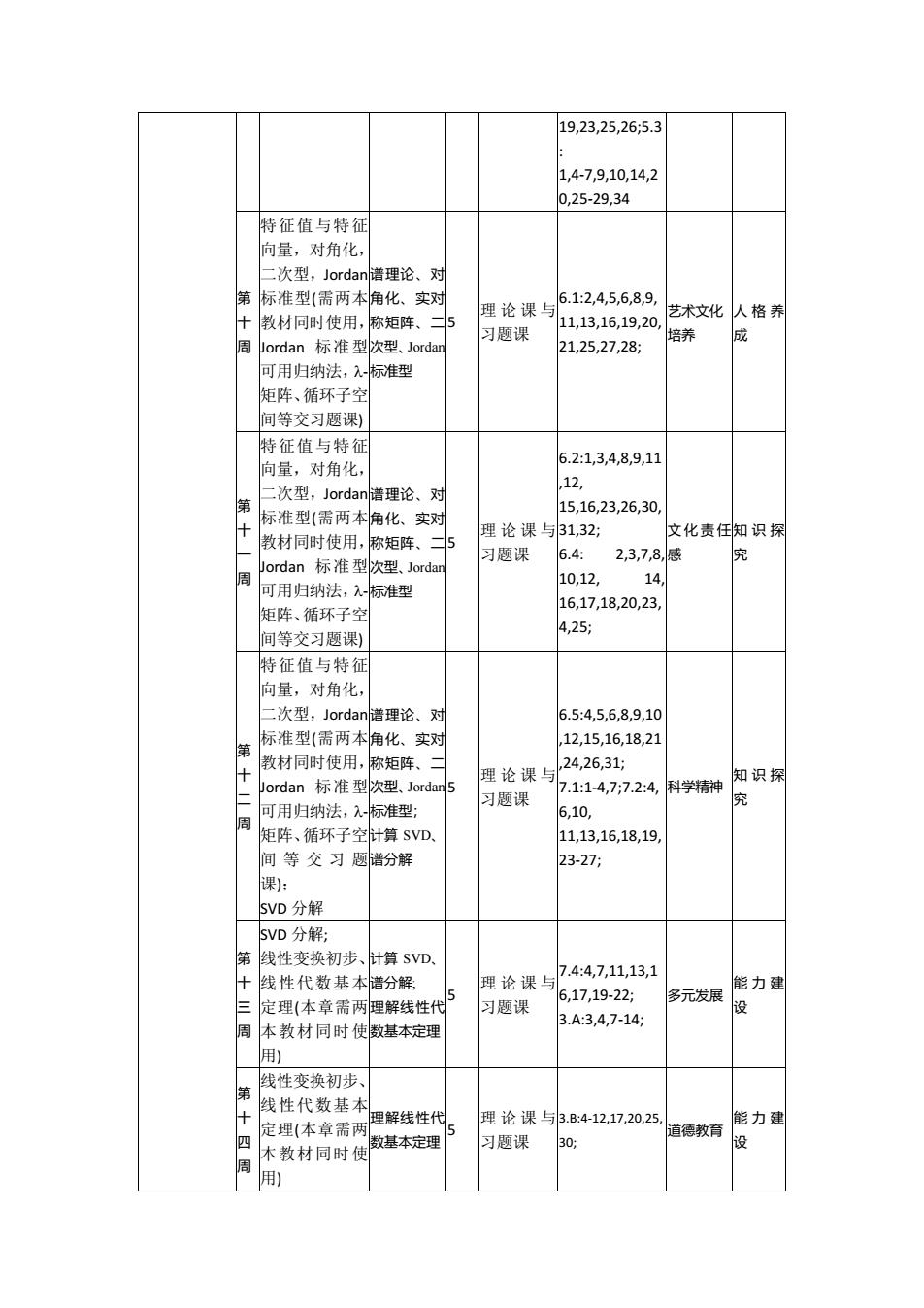
19,23,25,26;5.3 : 1,4-7,9,10,14,2 0,25-29,34 第 十 周 特征值与特征 向量,对角化, 二次型,Jordan 标准型(需两本 教材同时使用, Jordan 标准型 可用归纳法,- 矩阵、循环子空 间等交习题课) 谱理论、对 角化、实对 称矩阵、二 次型、Jordan 标准型 5 理论课与 习题课 6.1:2,4,5,6,8,9, 11,13,16,19,20, 21,25,27,28; 艺术文化 培养 人格养 成 第 十 一 周 特征值与特征 向量,对角化, 二次型,Jordan 标准型(需两本 教材同时使用, Jordan 标准型 可用归纳法,- 矩阵、循环子空 间等交习题课) 谱理论、对 角化、实对 称矩阵、二 次型、Jordan 标准型 5 理论课与 习题课 6.2:1,3,4,8,9,11 ,12, 15,16,23,26,30, 31,32; 6.4: 2,3,7,8, 10,12, 14, 16,17,18,20,23, 4,25; 文化责任 感 知识探 究 第 十 二 周 特征值与特征 向量,对角化, 二次型,Jordan 标准型(需两本 教材同时使用, Jordan 标准型 可用归纳法,- 矩阵、循环子空 间 等 交 习 题 课); SVD 分解 谱理论、对 角化、实对 称矩阵、二 次型、Jordan 标准型; 计算 SVD、 谱分解 5 理论课与 习题课 6.5:4,5,6,8,9,10 ,12,15,16,18,21 ,24,26,31; 7.1:1-4,7;7.2:4, 6,10, 11,13,16,18,19, 23-27; 科学精神 知识探 究 第 十 三 周 SVD 分解; 线性变换初步、 线性代数基本 定理(本章需两 本教材同时使 用) 计算 SVD、 谱分解; 理解线性代 数基本定理 5 理论课与 习题课 7.4:4,7,11,13,1 6,17,19-22; 3.A:3,4,7-14; 多元发展 能力建 设 第 十 四 周 线性变换初步、 线性代数基本 定理(本章需两 本教材同时使 用) 理解线性代 数基本定理 5 理论课与 习题课 3.B:4-12,17,20,25, 30; 道德教育 能力建 设
线性弯跪初步 第十五 线性代数基本 理解线性代 里论课 定理(本章需两 3.D:3,5,813,1 习题课17,20 学科知识 知识拉 数基本足理 本教材同时使 用) 六选讲 扩展阅读 5 理论课 课外阅读 可持续发价值 周 注1:建议按昭学周周学时推 使自动生成教学日历。 注2: 相应章节的课程思政融入点根据实际情况填写 示例 *考核方式(1】平时作到业20分 (Grading) (2)课程项目30分 (3)期末考试50分 (必含信息:教材名称,作者,出版社,出版年份,版次 ,书号) Introductionto Linear Algebra,G.Strang,Wellesley-Cambridge 教材或参考资 料(Textbooks Press,2016,第五版.ISBN:978-09802327-7-6 &Oh灯 Materials) .Linear algebra done right,,S.Axler,.Springer,2015,第二版ISBN g780387982588 矩阵理论与应用,张跃辉,科学出版社,2011,第一版,1SBN:9787030318138 其它(Morc) 备注(Notes) 备注说明: 1.带内容为必填项 2.课程简介字数为300-500字:课程大纲以表述清楚教学安排为宜,字数不限
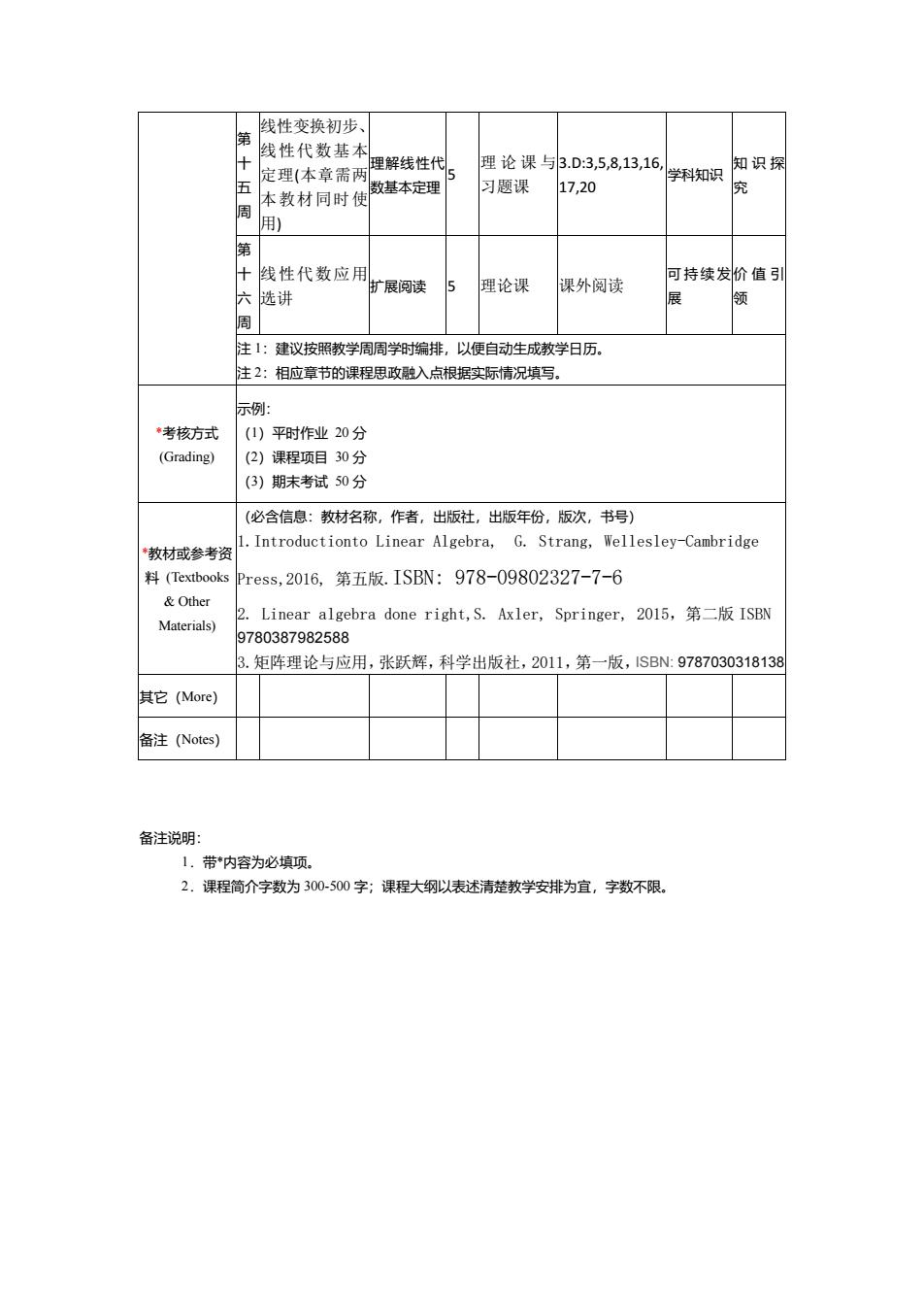
第 十 五 周 线性变换初步、 线性代数基本 定理(本章需两 本教材同时使 用) 理解线性代 数基本定理 5 理论课与 习题课 3.D:3,5,8,13,16, 17,20 学科知识 知识探 究 第 十 六 周 线性代数应用 选讲 扩展阅读 5 理论课 课外阅读 可持续发 展 价值引 领 注 1:建议按照教学周周学时编排,以便自动生成教学日历。 注 2:相应章节的课程思政融入点根据实际情况填写。 *考核方式 (Grading) 示例: (1)平时作业 20 分 (2)课程项目 30 分 (3)期末考试 50 分 *教材或参考资 料 (Textbooks & Other Materials) (必含信息:教材名称,作者,出版社,出版年份,版次,书号) 1.Introductionto Linear Algebra, G. Strang, Wellesley-Cambridge Press,2016, 第五版.ISBN: 978-09802327-7-6 2. Linear algebra done right,S. Axler, Springer, 2015,第二版 ISBN 9780387982588 3.矩阵理论与应用,张跃辉,科学出版社,2011,第一版,ISBN: 9787030318138 其它(More) 备注(Notes) 备注说明: 1.带*内容为必填项。 2.课程简介字数为 300-500 字;课程大纲以表述清楚教学安排为宜,字数不限